中南大学:《金属塑性加工原理》课程教学资源(PPT课件)第一篇 塑性变形力学基础 第2章 金属塑性变形的物性方程

第2章金属塑性变形的物性方程 §2.1金属塑性变形过程和力学特点 §2.2塑性条件方程 §2.3塑性应力应变关系(本构关系) §2.4变形抗力曲线与加工硬化 §2.5影响变形抗力的因素
第2章 金属塑性变形的物性方程 §2.1 金属塑性变形过程和力学特点 §2.2 塑性条件方程 §2.3 塑性应力应变关系(本构关系) §2.4 变形抗力曲线与加工硬化 §2.5 影响变形抗力的因素

§2.1金属塑性变形过程和力学特点 变形过程与特点 以单向拉伸为例说明塑性变形过程与特点,如图2-1所示。金属变形 分为弹性、均匀塑性变形、破裂三个阶段。 o<o,时,G=E8 。 当o≥0,以后,变形视作塑性阶段。σ一6是 非线性关系。当应力达到。之后,变形转为不均匀 塑性变形,呈不稳定状态。经短暂的不稳定变形 试样以断裂告终。 若在均匀塑性变形阶段出现卸载现象,一部分 变形得以恢复,另一部分则成为永久变形。卸载阶 段σ一8呈线性关系。这说明了塑性变形时,弹性 图2-1单向拉伸的塑性变形特点 变形依然存在。弹塑性共存与加载卸载过程不同的 G-8 关系是塑性变形的两个基本特征
§2.1 金属塑性变形过程和力学特点 − 变形过程与特点 以单向拉伸为例说明塑性变形过程与特点,如图2-1所示。金属变形 分为弹性、均匀塑性变形、破裂三个阶段。 s 时, = E 。 当 以后,变形视作塑性阶段。 是 非线性关系。当应力达到 之后,变形转为不均匀 塑性变形,呈不稳定状态。经短暂的不稳定变形, 试样以断裂告终。 s − b 若在均匀塑性变形阶段出现卸载现象,一部分 变形得以恢复,另一部分则成为永久变形。卸载阶 段 呈线性关系。这说明了塑性变形时,弹性 变形依然存在。弹塑性共存与加载卸载过程不同的 − 关系是塑性变形的两个基本特征。 −

由于加载、卸载规律不同,导致·一£关系不唯一。只有知道变形 历史,才能得到一一对应的σ一关系,即塑性变形与变形历史或路径 有关。这是第3个重要特征。 事实上,σ>o以后的点都可以看成是重新加载时的屈服点。以g点 为例,若卸载则σ一£关系为弹性。卸载后再加载,只要σ·,这一现象为 硬化或强化,是塑性变形的第4个显著特点。 在简单压缩下,忽略摩擦影响,得到的压缩σ:与拉伸σ基本相 同。但是若将拉伸屈服后的试样经卸载并反向加载至屈服,反向屈服 一般低于初始屈服。同理,先压后拉也有类似现象。这种正向变形强 化导致后继反向变形软化的现象称作Bauschinger效应。这是金属微观 组织变化所致。一般塑性理论分析不考虑Bauschingers效应。 Bridgman等人在不同的静水压力容器中做单向拉伸试验。结果表 明:静水压力只引起物体的体积弹性变形,在静水压力不很大的情况 下(与屈服极限同数量级)所得拉伸曲线与简单拉伸几乎一致,说明 静水压力对塑性变形的影响可以忽略
由于加载、卸载规律不同,导致 关系不唯一。只有知道变形 历史,才能得到一一对应的 关系,即塑性变形与变形历史或路径 有关。这是第3个重要特征。 事实上, 以后的点都可以看成是重新加载时的屈服点。以g点 为例,若卸载则 关系为弹性。卸载后再加载,只要 点, 关系仍为弹性。一旦超过g点, 呈非线性关系,即g点也是 弹塑性变形的交界点,视作继续屈服点。一般有 ,这一现象为 硬化或强化,是塑性变形的第4个显著特点。 − − s − − − g g s 在简单压缩下,忽略摩擦影响,得到的压缩 与拉伸 基本相 同。但是若将拉伸屈服后的试样经卸载并反向加载至屈服,反向屈服 一般低于初始屈服。同理,先压后拉也有类似现象。这种正向变形强 化导致后继反向变形软化的现象称作Bauschinger效应。这是金属微观 组织变化所致。一般塑性理论分析不考虑Bauschinger效应。 Bridgman等人在不同的静水压力容器中做单向拉伸试验。结果表 明:静水压力只引起物体的体积弹性变形,在静水压力不很大的情况 下(与屈服极限同数量级)所得拉伸曲线与简单拉伸几乎一致,说明 静水压力对塑性变形的影响可以忽略。 s s

基本假设 材料为均匀连续,且各向同性; 一体积变化为弹性的,塑性变形时体积不变; ,静水压力不影响塑性变形,只引起体积弹性变化; 一不考虑时间因素,认为变形为准静态; 不考虑Bauschinger?效应
基 本 假 设 ➢材料为均匀连续,且各向同性; ➢体积变化为弹性的,塑性变形时体积不变; ➢静水压力不影响塑性变形,只引起体积弹性变化; ➢不考虑时间因素,认为变形为准静态; ➢不考虑Bauschinger效应

s2.2塑性条件方程 屈服准则又称塑性条件(Plastic conditions)或屈服 条件(Yield conditions),它是描述不同应力状态下变形体 某点进入塑性状态并使塑性变形继续进行所必须满足的力学 条件。 用屈服函数(Yield function)表示: f(o)=0 (ij=x,y,2) f(o,)=0 (i=12,3) f(I1,I2,I3)=0 fI5,I)=0
§2.2 塑性条件方程 屈服准则又称塑性条件(Plastic conditions)或屈服 条件(Yield conditions),它是描述不同应力状态下变形体 某点进入塑性状态并使塑性变形继续进行所必须满足的力学 条件。 用屈服函数(Yield function)表示: ( ) 0 ( , , , ) ij f i j x y z = = ( ) 0 ( 1,2,3) i f i = = 1 2 3 f I I I ( , , ) 0 = 2 3 f I I ( , ) 0 =

Tresca 屈服准则 (最大剪应力准则) Imax=K 01-03=2k (01≥02≥03) Mises 屈服准则 0。=0, 回忆: g-万a-+o,-a+o-o .=5Va,-0,+o,-0+a-0+6G++
Tresca 屈服准则(最大剪应力准则) Mises 屈服准则 回忆: ] m x a = K 1 3 1 2 3 − = 2 ( ) k e s = 2 2 2 1 2 2 3 3 1 1 ( ) ( ) ( ) 2 e = − + − + − 1 2 2 2 2 2 2 ( ) ( ) ( ) 6( ) 2 e x y y z z x xy yz zx = − + − + − + + +

比较两屈服准则的区别: (1)物理含义不同:Tresca:最大剪应力达到极限值K Mises:畸变能达到某极限 (2)表达式不同; (3)几何表达不同: Tresca准则:在主应力空间中为一垂直m平面的正六棱柱; Mises准则:在主应力空间中为一垂直于π平面的圆柱。 (π平面:在主应力坐标系中,过原点并垂直于等倾线的平面)
比较两屈服准则的区别: (1)物理含义不同:Tresca:最大剪应力达到极限值K Mises :畸变能达到某极限 (2)表达式不同; (3)几何表达不同: Tresca准则:在主应力空间中为一垂直π平面的正六棱柱; Mises 准则:在主应力空间中为一垂直于π平面的圆柱。 (π平面:在主应力坐标系中,过原点并垂直于等倾线的平面)
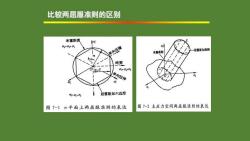
比较两屈服准则的区别 米塞斯圆 50>0 单向压缩 米塞则 冠雷斯加准斑 纯剪 单向拉伸 a>a 屈留斯加六边形 图7-1π平面上两屈服准则的表达 图?-2主应力空间两屈服准则的表达
比较两屈服准则的区别

两准则的联系: (1)空间几何表达:Mises圆柱外接于Tresca六棱柱; 在π平面上两准则有六点重合; (2) 通过引入罗德参数和中间主应力影响系数B,可以将两 准则写成 相同的形式: 01-O3=Bo B= 2 其中 √3+居 称为中间主应力影响系数 202-01-03 01-03 称为Lode参数
两准则的联系: (1)空间几何表达:Mises圆柱外接于Tresca六棱柱; 在π平面上两准则有六点重合; (2)通过引入罗德参数和中间主应力影响系数β,可以将两 准则写成 相同的形式: 其中 称为中间主应力影响系数 称为Lode参数。 1 3 − = s 2 2 3 = + 213 1 3 2 − − = −

讨论:①当材料受单向应力时,B=1,两准则重合; ②在纯剪应力作用下,两准则差别最大; 按Tresca准则: 无 按Mises?准则: 2 ③一般情况下,B=1-1.154
讨论:① 当材料受单向应力时,β=1,两准则重合; ② 在纯剪应力作用下,两准则差别最大; 按Tresca准则: 按Mises准则: ③ 一般情况下,β=1-1.154
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 中南大学:《金属塑性加工原理》课程教学资源(PPT课件)第一篇 塑性变形力学基础 第1章 应力分析与应变分析.pptx
- 中南大学:《金属塑性加工原理》课程教学资源(PPT课件)绪论 Principle of Plastic Deformation in Metal Processing.pptx
- 北京城市学院:《建筑工程材料》课程教学课件(PPT讲稿)09 装饰材料.ppt
- 北京城市学院:《建筑工程材料》课程教学课件(PPT讲稿)08 沥青及防水材料.ppt
- 北京城市学院:《建筑工程材料》课程教学课件(PPT讲稿)07 墙体与屋面材料.ppt
- 北京城市学院:《建筑工程材料》课程教学课件(PPT讲稿)06 建筑钢材.ppt
- 北京城市学院:《建筑工程材料》课程教学课件(PPT讲稿)05 建筑砂浆.ppt
- 北京城市学院:《建筑工程材料》课程教学课件(PPT讲稿)04 混凝土.ppt
- 北京城市学院:《建筑工程材料》课程教学课件(PPT讲稿)03 水泥.ppt
- 北京城市学院:《建筑工程材料》课程教学课件(PPT讲稿)02 气硬性胶凝材料.ppt
- 北京城市学院:《建筑工程材料》课程教学课件(PPT讲稿)01 建筑材料的基本性质.ppt
- 北京城市学院:《建筑工程材料》课程教学课件(PPT讲稿)10 其他建材与新型建材.ppt
- 北京城市学院:《建筑工程材料》课程教学课件(PPT讲稿)00 建筑材料绪论 Construction Materials.ppt
- 北京城市学院:《建筑工程材料》课程教学实验指导书(建筑材料,共十个实验).doc
- 北京城市学院:《建筑工程材料》课程教学资源(试卷习题)试卷(2011)答案.doc
- 北京城市学院:《建筑工程材料》课程教学资源(试卷习题)试卷(2010)答案.doc
- 北京城市学院:《建筑工程材料》课程教学资源(试卷习题)试卷(2011)试题.doc
- 北京城市学院:《建筑工程材料》课程教学资源(试卷习题)试卷(2010)试题.doc
- 《建筑工程材料》课程教学资源(学习指导)08 墙体材料.doc
- 《建筑工程材料》课程教学资源(学习指导)07 沥青及防水材料.doc
- 中南大学:《金属塑性加工原理》课程教学资源(PPT课件)第一篇 塑性变形力学基础 第3章 金属塑性加工的宏观规律.pptx
- 中南大学:《金属塑性加工原理》课程教学资源(PPT课件)第一篇 塑性变形力学基础 第4章 金属塑性加工的摩擦与润滑.pptx
- 中南大学:《金属塑性加工原理》课程教学资源(PPT课件)第三篇 塑性变形材料学基础 第5章 金属的塑性(主讲:张新明).pptx
- 中南大学:《金属塑性加工原理》课程教学资源(PPT课件)第三篇 塑性变形材料学基础 第6章 塑性加工过程的组织性能变化和温度——速度条件.pptx
- 中南大学:《金属塑性加工原理》课程教学资源(PPT课件)第四篇 金属塑性变形力学解析方法 第7章 金属塑性加工变形力的工程法解析.pptx
- 中南大学:《金属塑性加工原理》课程教学资源(PPT课件)第四篇 金属塑性变形力学解析方法 第8章 滑移线理论及应用.pptx
- 中南大学:《金属塑性加工原理》课程教学资源(PPT课件)第四篇 金属塑性变形力学解析方法 第9章 功平衡法和上限法及其应用.pptx
- 中国天然橡胶供给状况及前景(橡胶基础会议,2013年11月).pptx
- 山东理工大学:《结晶学》课程教学资源(课件讲稿)10 晶体结构.pdf
- 山东理工大学:《结晶学》课程教学资源(课件讲稿)09 晶体化学基础(2/2).pdf
- 山东理工大学:《结晶学》课程教学资源(课件讲稿)09 晶体化学基础(1/2).pdf
- 山东理工大学:《结晶学》课程教学资源(课件讲稿)08 晶体结构的几何理论.pdf
- 山东理工大学:《结晶学》课程教学资源(课件讲稿)07 实际晶体的形态.pdf
- 山东理工大学:《结晶学》课程教学资源(课件讲稿)06 晶体定向和结晶符号.pdf
- 山东理工大学:《结晶学》课程教学资源(课件讲稿)05 单形和聚形.pdf
- 山东理工大学:《结晶学》课程教学资源(课件讲稿)04 晶体的宏观对称.pdf
- 山东理工大学:《结晶学》课程教学资源(课件讲稿)03 晶体的面角恒等和投影.pdf
- 山东理工大学:《结晶学》课程教学资源(课件讲稿)02 晶体生长的基本规律.pdf
- 山东理工大学:《结晶学》课程教学资源(课件讲稿)01 绪论.pdf
- 《结晶学》课程教学资源(PPT课件)结晶学复习与思考.ppt
