《概率论与数理统计》课程教学资源(PPT课件)第一章 概率论的基本概念 第六节 独立性

概奉伦论与散理统计 第六节 独立性 一、事件的相互独立性 二、几个重要定理 三、例题讲解 四、小结
一、事件的相互独立性 二、几个重要定理 三、例题讲解 四、小结 第六节 独立性

概率论与款理统外 一、事件的相互独立性 1.引例 盒中有5个球(3绿2红),每次取出一个,有放回 地取两次.记 A=第一次抽取,取到绿球, B=第二次抽取,取到绿球, 则有 P(BA)=P(B), 它表示A的发生并不影响B发生的可能性大小. P(BA)=P(B)P(AB)=P(A)P(B)
一 、事件的相互独立性 , , , , . 5 (3 2 ), , 第二次抽取 取到绿球 第一次抽取 取到绿球 地取两次 记 盒中有 个球 绿 红 每次取出一个 有放回 B A 则有 P(B A) P(B), 它表示 A的发生并不影响 B 发生的可能性大小. P(B A) P(B) P(AB) P(A)P(B) 1.引例

概奉论与散理统计「 2.定义 设A,B是两事件,如果满足等式 P(AB)=P(A)P(B) 则称事件A,B相互独立,简称A,B独立. 说明 事件A与事件B相互独立,是指事件A的 发生与事件B发生的概率无关
, , , . ( ) ( ) ( ) , , 则称事件 相互独立 简称 独立 设 是两事件 如果满足等式 A B A B P AB P A P B A B 事件 A 与 事件 B 相互独立,是指事件 A 的 发生与事件 B 发生的概率无关. 说明 2.定义

概率伦与敖理统外 请同学们思考 两事件相互独立与两事件互斥的关系. 两事件相互独立P(AB)=P(A)P(B): 二者之间没 两事件互斥 AB=☑ 有必然联系 例如 B 若P=P(B剧 AB 则P(AB)=P(A)P(B). 由此可见两事件相互独立,但两事件不互斥
两事件相互独立 P(AB) P(A)P(B) 两事件互斥 AB A B , 2 1 , ( ) 2 1 若 P(A) P B AB 则 P(AB) P(A)P(B). 例如 由此可见两事件相互独立,但两事件不互斥. 两事件相互独立与两事件互斥的关系. 请同学们思考 二者之间没 有必然联系
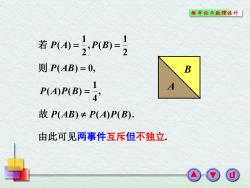
概奉论与散理统计「 若P0P®-} 则P(AB)=0, B PAPB, 故P(AB)≠P(A)P(B): 由此可见两事件互斥但不独立
A B 2 1 , ( ) 2 1 若 P(A) P B 故 P(AB) P(A)P(B). 由此可见两事件互斥但不独立. 则 P(AB) 0, , 4 1 P(A)P(B)

概率伦与敖理统外 3.三事件两两相互独立的概念 定义设A,B,C是三个事件,如果满足等式 P(AB)=P(A)P(B), P(BC)=P(B)P(C), P(AC)=P(A)P(C), 则称事件A,B,C两两相互独立
3.三事件两两相互独立的概念 , , . ( ) ( ) ( ), ( ) ( ) ( ), ( ) ( ) ( ), , , , 则称事件 两两相互独立 定义 设 是三个事件 如果满足等式 A B C P AC P A P C P BC P B P C P AB P A P B A B C

概奉论与散理统计「 4.三事件相互独立的概念 定义设A,B,C是三个事件,如果满足等式 P(AB)=P(A)P(B), P(BC)=P(B)P(C), P(AC)=P(A)P(C), P(ABC)=P(A)P(B)P(C), 则称事件A,B,C相互独立· 注意 三个事件相互独立 2三个事件两两相互独立
注意 三个事件相互独立 三个事件两两相互独立 4.三事件相互独立的概念 , , . ( ) ( ) ( ) ( ), ( ) ( ) ( ), ( ) ( ) ( ), ( ) ( ) ( ), , , , 则称事件 相互独立 定义 设 是三个事件 如果满足等式 A B C P ABC P A P B P C P AC P A P C P BC P B P C P AB P A P B A B C

概率伦与数理统外 推广设A1,A2,An是n个事件,如果对于任意 k(1<k≤n),任意1≤i1<i2<.<ik≤n,具有等式 P(AA2.A)=P(A)P(A,).P(A), 则称A1,A,An为相互独立的事件 n个事件相互独立 n个事件两两相互独立
( ) ( ) ( ) ( ), 1 2 k 1 2 k P Ai Ai Ai P Ai P Ai P Ai , , , . 则称 A1 A2 A n 为相互独立的事件 n 个事件相互独立 n个事件两两相互独立 任意 具有等式 设 是 个事件 如果对于任意 (1 ), 1 , , , , , 1 2 1 2 k k n i i i n A A A n k n 推广

概奉论与散理统计 二、几个重要定理 定理一设A,B是两事件,且P(A)>0.若A,B相 互独立,则P(BA)=P(B).反之亦然, 证明 P(BA)= P(AB) P(A) P(A)P(B)=P(B) P(A) →P(BA)=P(B):
证明 ( ) ( ) ( ) P A P AB P B A ( ) ( ) ( ) ( ) P B P A P A P B P(B A) P(B). , ( ) ( ). . , , ( ) 0. , 互独立 则 反之亦然 设 是两事件 且 若 相 P B A P B A B P A A B 二、几个重要定理 定理一

概率论与数理统外 定理二若A,B相互独立,则下列各对事件, A与B,A与B,A与B也相互独立. 证明 先证A与B独立. 因为A=ABUAB且(AB)(AB)=, 所以P(A)=P(AB)+P(AB), 即PAB)=P(A)-PAB)
证明 先证 A 与 B 独立. 因为 A AB AB 且 (AB)(AB) , 所以 P(A) P(AB) P(AB), 即 P(AB) P(A) P(AB). , , . , , , 与 与 与 也相互独立 若 相互独立 则下列各对事件 A B A B A B 定理二 A B
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《概率论与数理统计》课程教学资源(PPT课件)第一章 概率论的基本概念 第五节 条件概率.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第一章 概率论的基本概念 第四节 等可能概型(古典概型).ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第一章 概率论的基本概念 第三节 频率与概率.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第一章 概率论的基本概念 第二节 样本空间、随机事件.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第一章 概率论的基本概念 第一节 随机试验.ppt
- 石河子大学:《概率论与数理统计》课程教学大纲 Probability Theory and Mathematical Statistics.doc
- 石河子大学:《概率论与数理统计》课程教综合练习册(无答案).doc
- 石河子大学:《概率论与数理统计》课程授课教案(负责人:马金凤).doc
- 石河子大学:《概率论与数理统计》课程教学大纲 Probability Theory and Mathematical Statistics.doc
- 《概率论与数理统计》课程教学资源(实验指导)概率论与数理统计实践指导书.doc
- 西安交通大学:《概率论与数理统计》课程教学课件(PPT讲稿)概率论与数理统计重点与疑难问题选讲(梅长林).ppt
- 南开大学:《概率论与数理统计》课程教学资源(讲义)从随机变量到随机过程(主讲:王永进).pdf
- 西安电子科技大学:《概率论与数理统计》课程教学课件(讲稿)第八章 假设检验 8.3 正态总体方差的假设检验 8.6 分布拟合检验.pdf
- 西安电子科技大学:《概率论与数理统计》课程教学课件(讲稿)第八章 假设检验 8.1 假设检验 8.2 正态总体均值的假设检验.pdf
- 西安电子科技大学:《概率论与数理统计》课程教学课件(讲稿)第七章 参数估计 7.4 区间估计 7.5 正态总体均值和方差的区间估计 7.6(0-1)分布参数的区间估计 7.7 单侧置信区间.pdf
- 西安电子科技大学:《概率论与数理统计》课程教学课件(讲稿)第七章 参数估计 7.3 估计量的评选标准 7.4 区间估计.pdf
- 西安电子科技大学:《概率论与数理统计》课程教学课件(讲稿)第七章 参数估计 7.1 点估计 7.2 基于截尾样本的最大似然估计.pdf
- 西安电子科技大学:《概率论与数理统计》课程教学课件(讲稿)第六章 样本及抽样分布 6.3 抽样分布.pdf
- 西安电子科技大学:《概率论与数理统计》课程教学课件(讲稿)第六章 样本及抽样分布 6.1 随机样本 6.2 直方图和箱线图.pdf
- 西安电子科技大学:《概率论与数理统计》课程教学课件(讲稿)第五章 大数定律及中心极限定理.pdf
- 《概率论与数理统计》课程教学资源(PPT课件)第一章 概率论的基本概念(习题课).ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第二章 随机变量及其分布 第一节 随机变量.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第二章 随机变量及其分布 第二节 离散型随机变量及其分布律.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第二章 随机变量及其分布 第三节 随机变量的分布函数.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第二章 随机变量及其分布 第四节 连续型随机变量及其概率密度.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第二章 随机变量及其分布 第五节 随机变量的函数的分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布 第一节 二维随机变量.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布 第二节 边缘分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布 第三节 条件分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布 第四节 相互独立的随机变量.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布 第五节 两个随机变量的函数的分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布(习题课).ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第四章 随机变量的数字特征 第一节 数学期望.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第四章 随机变量的数字特征 第二节 方差.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第四章 随机变量的数字特征 第三节 协方差及相关系数.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第四章 随机变量的数字特征 第四节 矩、协方差矩阵.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第四章 随机变量的数字特征(习题课).ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第五章 大数定律及中心极限定理 第一节 大数定律.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第五章 大数定律及中心极限定理 第二节 中心极限定理.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第五章 大数定律及中心极限定理(习题课).ppt
