《数理统计》课程PPT教学课件（讲稿）常见的连续性随机变量的分布

常见的连续性随机变量的分布 (1)均匀分布若X的df为 a<x<b 0, 其他 则称X服从区间(a,b)上的均匀分布或称 X服从参数为a,b的均匀分布.记作 X~U(a,b)

(1) 均匀分布 常见的连续性随机变量的分布 若 X 的 d.f. 为        = − 0, 其他 , 1 ( ) a x b f x b a 则称 X 服从区间( a , b)上的均匀分布或称 X ~ U(a,b) X 服从参数为 a , b的均匀分布. 记作

X的分布函数为 x<a, F=m- a≤x≤b: h-a X≥b

X 的分布函数为        − − = 1 , 0, b a x a x b a x b x a     , , − = x F(x) f (t) dt

f(x) F(x)

x f ( x) a b x F( x) a b

V(c,d)E(a,b),P(c<X<d)=d dx= d-c b-a 即X落在(a,b)内任何长为dc的小区间的 概率与小区间的位置无关，只与其长度成正 比.这正是几何概型的情形 应用场合 进行大量数值计算时，若在小数点后第 k位进行四舍五入，则产生的误差可以看作 服从 -100 的水随机变量

(c,d)  (a,b), x b a P c X d d 1 ( ) d c −   = b a d c − − = 即 X 落在(a,b)内任何长为 d – c 的小区间的 概率与小区间的位置无关, 只与其长度成正 比. 这正是几何概型的情形. 进行大量数值计算时, 若在小数点后第 k 位进行四舍五入, 则产生的误差可以看作 服从  的 r.v. 随机变量      − −k −k U 10 2 1 10 , 2 1 应用场合

(2)指数分布 若X的dlf为 ,x>0 见>0为常数 其他 则称X服从参数为入的指数分布 记作X~E(2) X<0 X的分布函数为

(2) 指数分布 若 X 的d.f. 为     = − 0, 其他 , 0 ( ) e x f x x  则称 X 服从 参数为  的指数分布 记作 X ~ E() X 的分布函数为    −   = − 1 , 0 0, 0 ( ) e x x F x x  > 0 为常数

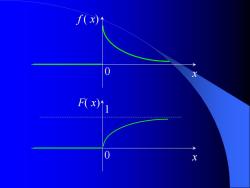
f(x) F(x

1 x F( x ) 0 x f ( x ) 0

对于任意的0<a<b, P(a<X<b)=[Re-"dx =F(b)-F(a) e-a e-1b 应用场合 用指数分布描述的实例有： 随机服务系统中的服务时间 电话问题中的通话时间 无线电元件的寿命 指数分布 常作为各种“寿命 动物的寿命 分布的近似

对于任意的 0 < a < b, a b b a x e e F b F a P a X b e x     − − − = − = −   =  ( ) ( ) ( ) d 应用场合 用指数分布描述的实例有： 随机服务系统中的服务时间 电话问题中的通话时间 无线电元件的寿命 动物的寿命 指数分布 常作为各种“寿命” 分布的近似

(3)正态分布 若X的df为 (x-)2 2o3 一 00 (Gauss)分布 则称X服从参数为 2的正态分布 记作X~N( 2

(3) 正态分布 若X 的 d.f. 为 = −    + − − f x e x x 2 2 2 ( ) 2 1 ( )    则称 X 服从参数为 , 2 的正态分布 记作 X ~ N ( , 2 ) , 为常数，   0 亦称高斯 (Gauss)分布

N(-3,1.2) 0.3 0.25 0.2 0.15 0.1 05 -6-5-4-3 -2 -1 4=-3

N (-3 , 1.2 ) - 6 - 5 - 4 - 3 - 2 - 1 0.05 0.1 0.15 0.2 0.25 0.3  = −3

f(x)的性质 口图形关于直线x=对称，即 f(4+x)=f(u-x) 在x=u时，f(x)取得最大值 2π0 在x=u士o时，曲线y=f(x)在对应的 点处有拐点 曲线y=f(x)以x轴为新近线 曲线y=f(x)的图形星单峰状

f (x) 的性质： ❑ 图形关于直线 x =  对称, 即 在 x =  时, f (x) 取得最大值 2 1 在 x = ± 时, 曲线 y = f (x) 在对应的 点处有拐点 曲线 y = f (x) 以 x 轴为渐近线 曲线 y = f (x) 的图形呈单峰状 f ( + x) = f ( - x)