《计算机应用基础》课程教学资源（PPT课件讲稿）第二篇 系统平台与计算环境_第四章 数值与信息编码_第四章 数制与信息编码

SHANDONG 4数制与信息编码 UNIVERS 1.数制及其转换 TY OF 2.数值型数据的表示及处理 3.文字的表示及处理 4.多媒体信息的表示及处理

4 数制与信息编码 1. 数制及其转换 2. 数值型数据的表示及处理 3. 文字的表示及处理 4. 多媒体信息的表示及处理 1

4数制与信息编码 SHANDONG UNIVERSITY OF TECHNOLOGY 1.数值信息 2.文字信息 3.多媒体信息 2

1. 数值信息 2. 文字信息 3. 多媒体信息 2 4 数制与信息编码

数值信息的表示 SHANDONG UNIVERSITY OF TECHNOLOGY ■ 计数：十进制。 ■计时：六十进制。 ■月到年的进制：十二进制。 ■季度到年的进制：四进制。 在计算机内部用二进制数码表示 各种数据，在计算机程序的编写中有 时采用八进制和十六进制。 3

数值信息的表示 ◼ 计数：十进制。 ◼ 计时：六十进制。 ◼ 月到年的进制：十二进制。 ◼ 季度到年的进制：四进制。 在计算机内部用二进制数码表示 各种数据，在计算机程序的编写中有 时采用八进制和十六进制。 3

数值信息的表示 SHANDONG UNIVERSITY OF TECHNOLOGY ■数码：一组用来表示某种数制的符号。 ■ 基数：数制所使用的数码个数称为“基数”或 “基”，常用“R”表示，称R进制。 十进制 R=10,包含数码：0,1,2,3,4,5,6,7,8,9 二进制 R=2, 包含数码：0,1 八进制 R=8, 包含数码：0,1,2,3,4,5,6,7 十六进制R=16，包含数码：0，9，A,B,C,D,E,F “逢R进一，借一当R》 4

数值信息的表示 ◼ 数码：一组用来表示某种数制的符号。 ◼ 基数：数制所使用的数码个数称为“基数”或 “基”，常用“R”表示，称R进制。 十进制 R=10， 包含数码:0,1,2,3,4,5,6,7,8,9 二进制 R=2 ， 包含数码: 0,1 八进制 R=8 ， 包含数码: 0,1,2,3,4,5,6,7 十六进制 R=16 ，包含数码: 0,.,9,A,B,C,D,E,F “逢R进一，借一当R” 4

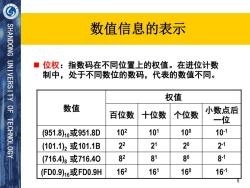
数值信息的表示 SHANDONG UNIVERSITY OF ■位权：指数码在不同位置上的权值。在进位计数 制中，处于不同数位的数码，代表的数值不同。 权值 数值 百位数 十位数 个位数 小数点后 TECHNOLOGY 一位 (951.8)10或951.8D 102 101 100 101 (101.1)2或101.1B 22 21 20 21 (716.4)8或716.40 82 81 80 81 (FD0.9)16或FD0.9H 162 161 160 161 5

数值信息的表示 ◼ 位权：指数码在不同位置上的权值。在进位计数 制中，处于不同数位的数码，代表的数值不同。 数值 权值 百位数 十位数 个位数 小数点后 一位 (951.8)10或951.8D 102 101 100 10-1 (101.1)21或101.1B 2 2 2 1 2 0 2 -1 (716.4)81或716.4O 8 2 8 1 8 0 8 -1 (FD0.9)16或FD0.9H 162 161 160 16-1 5

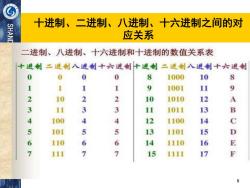
十进制、二进制、八进制、十六进制之间的对 应关系 二进制、八进制、十六进制和十进制的数值关系表 十进制二进喇八进制十六进制十进制二进制入进制十六进制 0 0 0 0 8 1000 10 8 1 1 1 9 1001 11 9 2 10 2 10 1010 12 A 3 1山 3 3 11 1011 13 B 4 100 4 4 12 1100 14 C 5 101 5 5 13 1101 15 D 6 110 6 6 14 1110 16 E 7 111 7 15 1111 17 F 6

十进制、二进制、八进制、十六进制之间的对 应关系 6

SHANDONG 2.数制的转换 十进制 二进制、八进制、十六进制数转化为十进制数 UNIVERSI ●对于任何一个二进制数、八进制数、十六进制数可以写出它的按 权展开式，再进行计算即可。 ●例如： (1111.11)2 =1×23+1×22+1×21+1×20+1×21+1×22=15.75 TECHNOLOG (A10B.8)16 =10×163+1×162+0×161+11×160+8×161=41227.5 1

2.数制的转换 ◼ 二进制、八进制、十六进制数转化为十进制数 ⚫ 对于任何一个二进制数、八进制数、十六进制数可以写出它的按 权展开式，再进行计算即可。 ⚫ 例如： （1111.11）2 = 1×2 3+1×2 2+1×2 1+1×2 0 +1×2 -1 +1×2 -2=15.75 （A10B.8）16 =10×163 + 1×162+ 0×161 +11×160 +8×16-1= 41227.5 7 十进制

十进制数转化为R进制 R进制 SHANDONG UNIVERSITY OF TECHNOLOGY 对于整数部分采用除R取余法，即逐次除以R,直至 商为0，得出的余数倒排，即为R进制各位的数码。 示例1：十进制转换为八进制 最低位 8 75 3 (75)=(113) 8 9 1 (113)8 8 =1×82+1×81+3×80 最高位 8

十进制数转化为R进制数 ◼ 对于整数部分采用除R取余法，即逐次除以R，直至 商为0，得出的余数倒排，即为R进制各位的数码。 (75)10=(113)8 示例1：十进制转换为八进制 75 9 1 8 8 8 3 1 1 0 最高位 最低位 （113）8 =1×8 2＋1×8 1＋3×8 0 8 R进制

十进制数转化为R进制数 SHANDONG UNIVERSITY OF TECHNOLOGY 示2：中进制名 二进制 2175 1 237 1 2 18 0 (75)。=(1001011)2 2 9 1 2 4 0 (1001011)2 =1×26+1X23+1×2 2 2 0 +1×20 2 1 1 最高位 9

十进制数转化为R进制数 示例2:十进制转换为二进制 (75)10 = (1001011)2 75 37 18 9 4 2 1 0 1 1 1 1 0 0 0 2 2 2 2 2 2 2 最低位 最高位 (1001011)2 ＝1×2 6＋1×2 3＋1×2 1 ＋1×2 0 9

十进制数转化为R进制数 SHANDONG UNIVERSITY OF TECHNOLOGY 小数部分采用乘R取整法，即逐次乘以R,当积为0或达到所要 求的精度时，将每次乘积的整数部分由上而下排列。 示例： 0.3125 2 0.6250 最高位 × 2 1.2500 (0.3125)10=(0.0101)2 × 2 (0.0101)2 0.5000 =1×2-2+1×24 2 最低位 1.0000 10

十进制数转化为R进制数 ◼ 小数部分采用乘R取整法，即逐次乘以R，当积为0或达到所要 求的精度时，将每次乘积的整数部分由上而下排列。 (0.3125)10 =(0.0101)2 0. 3125 × 2 0. 6250 × 2 1. 2500 × 2 1. 0000 0. 5000 × 2 最高位 最低位 0 1 1 0 示例: (0.0101)2 =1×2 -2＋1×2 -4 10