上海交通大学：《电路基础》课程教学资源（PPT课件）第三章 电路定理 §3.4 互易定理

上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY 电路基础 第三章 电路定理 上海交通大学本科学位课程 1B三G

电路基础 上海交通大学本科学位课程 第三章 电路定理

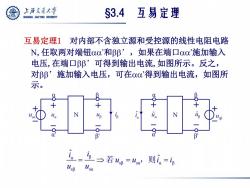
上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY §3.4互易定理 互易定理1 对内部不含独立源和受控源的线性电阻电路 N,任取两对端钮oo'和βB’,如果在端口oo'施加输入 电压，在端口ββ’可得到输出电流，如图所示。反之， 对Bβ’施加输入电压，可在00得到输出电流，如图所 示。 N B N in B' B → 若4B=ua’则。=

§3.4 互易定理 互易定理1 对内部不含独立源和受控源的线性电阻电路 N,任取两对端钮 ’和’ ，如果在端口 ’施加输入 电压,在端口’可得到输出电流,如图所示。反之， 对’施加输入电压，可在 ’得到输出电流，如图所 示。 α β sβ sα α β sβ sα ˆ    ˆ  i i u u i i u u 若 ，则

上游文通大学 互易定理 SHANGHAI JIAO TONG UNIVERSITY S3.4 证明：设电路中有b条支路，连接o0’ 和ββ’的支路电压和电流分别 为 ua ia upy if ie i it ip 根据特勒根定理 u+42+∑4，f=0 i.+p+∑i=0 由于电路N由线性非时变电阻组成，所以 山k=Ri,e=Rie 则有 ui.+g6+∑R,=0 i。+i+∑R,i4.=0 + ui。+42=i。+i6 4=4sa’4g=0,i。=0,ig=弘sB 4。=4p4→ N (一 B 因此， 当弘sB=从su时，ia=3

证明：设电路中有b条支路，连接’和’的支路电压和电流分别 为 α α β β u ，i ，u ，i ， α αˆ uˆ ，i ， β βˆ uˆ ，i 根据特勒根定理 α α u ˆi  β β u ˆi  1 ˆ 0 b k k k u i   α α uˆ i  β β uˆ i  1 ˆ 0 b k k k u i   由于电路N由线性非时变电阻组成，所以 ˆ ˆ k k k k k k u  R i ，u  R i 则有 α α u ˆi  β β u ˆi  1 ˆ 0 b k k k k R i i   α α uˆ i  β β uˆ i  1 ˆ 0 b k k k k R i i   α α u ˆ  i  β β u ˆi  α α uˆ i  β β uˆ i α β Sα α Sβ β sβ sα ˆ  ˆ    i i u i u i u u Sβ Sα α β u u ˆ 因此，当  时，i  i α Sα β α β Sβ  u  u ，u  0，uˆ  0，uˆ  u §3.4 互易定理

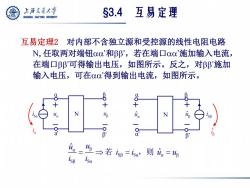
上游充通大兽 §3.4 互易定理 SHANGHAI JIAO TONG UNIVERSITY 互易定理2 对内部不含独立源和受控源的线性电阻电路 N,任取两对端钮αo'和BB',若在端口oo'施加输入电流， 在端口β邹'可得输出电压，如图所示。反之，对βB施加 输入电压，可在00'得到输出电流，如图所示。 8 B N up N a B' B' 。= →若isp=sa,则da=

互易定理2 对内部不含独立源和受控源的线性电阻电路 N,任取两对端钮 ’和’ ，若在端口 ’施加输入电流， 在端口’可得输出电压，如图所示。反之，对’施加 输入电压，可在 ’得到输出电流，如图所示。 α β Sβ Sα α β Sβ Sα ˆ    ˆ  u u i i u u i i 若 ，则 §3.4 互易定理

上游充通大兽 互易定理 SHANGHAI JIAO TONG UNIVERSITY 3.4 证明方法同定理1 B 8 + N N β' B' 根据特勒根定理有 uala upl tala igip i。=-ia’6=0,。=0,g=-is .-4sp=-i→ 立= isp isa 因此，当$=s时，元。=4

证明方法同定理1 α α u ˆi  β β u ˆi  α α uˆ i  β β uˆ i 根据特勒根定理有 α Sα β α β Sβ  i  i ，i  0，iˆ  0，iˆ  i α β β Sβ α Sα Sβ Sα ˆ     ˆ   u u u i u i i i Sβ Sα α β 因此，当i  i 时，uˆ  u §3.4 互易定理

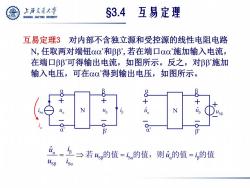
上游文通大学 互易定理 SHANGHAI JIAO TONG UNIVERSITY S3.4 互易定理3 对内部不含独立源和受控源的线性电阻电路 N,任取两对端钮oo'和βB',若在端口oo'施加输入电流， 在端口ββ'可得输出电流，如图所示。反之，对Bβ'施加 输入电压，可在00'得到输出电压，如图所示。 + N N B' B i →若4的值=s的值，则i的值=的值

互易定理3 对内部不含独立源和受控源的线性电阻电路 N,任取两对端钮 ’和’ ,若在端口 ’施加输入电流， 在端口’可得输出电流，如图所示。反之，对’施加 输入电压，可在 ’得到输出电压，如图所示。 α β Sβ Sα α β Sβ Sα ˆ    ˆ  u i u i u i u i 若 的值 的值，则 的值 的值 §3.4 互易定理

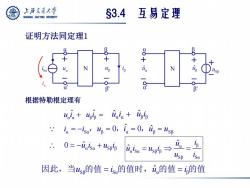
上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY S3.4 互易定理 证明方法同定理1 B N N 十 SB a' β' g B' 根据特勒根定理有 uala+urlg iala iptp i。=-is4=0,n=0,ip=山sp .0=-5a+弘sB3 i3sa=4sB3→ usB isa 因此，当4s的值=s的值时，i的值=的值

证明方法同定理1 α α u ˆi  β β u ˆi  α α uˆ i  β β uˆ i 根据特勒根定理有 α Sα β α β Sβ ˆ  i  i ，u  0，i  0，uˆ  u α Sa Sβ β  0  uˆ i  u i α β α Sα Sβ β Sβ Sα ˆ ˆ    u i u i u i u i Sβ Sα α β 因此，当u 的值  i 的值时，uˆ 的值  i 的值 §3.4 互易定理

上游充通大兽 SHANGHAI JIAO TONG UNIVERSITY §3.4 互易定理 互易定理的适用范围是比较窄的，它只适用于无源线性非时 变电路。如果电路中有独立源或受控源，非线性元件，时变 元件等，该电路就不能运用互易定理。这是因为线性非时变 电路保证了电路的电阻矩阵和电导矩阵具有对称性，才使互 易性得以成立。 u2≠0 41=0 uw2≠0 =0

§3.4 互易定理 互易定理的适用范围是比较窄的，它只适用于无源线性非时 变电路。如果电路中有独立源或受控源，非线性元件，时变 元件等，该电路就不能运用互易定理。这是因为线性非时变 电路保证了电路的电阻矩阵和电导矩阵具有对称性，才使互 易性得以成立。 u2≠0 u1=0 u2≠0 u1=0

上游充通大学 S3.4互易定理 SHANGHAI JIAO TONG UNIVERSITY 互易定理在应用时要注意，前两种形式中，当激励是 电压，响应为电流；当激励是电流，响应就是电压； 第3种形式，一边激励、响应都是电流，另一边激励、 响应都是电压。从总体上说，不能全是电流或全是电 压。（注意，互易定理中各次观测的响应均为零状态 响应) 应用互易定理时，不仅有量的大小问题，而且还有方 向问题。一般电源的移动方法为：平移法和旋转法。 互易定理用于解平衡电桥电路和对称电路较方便。 互易性与无源性是互不相干的，回转器是无源器件， 但不能互易

互易定理在应用时要注意，前两种形式中，当激励是 电压，响应为电流；当激励是电流，响应就是电压； 第3 种形式，一边激励、响应都是电流，另一边激励、 响应都是电压。从总体上说，不能全是电流或全是电 压。(注意，互易定理中各次观测的响应均为零状态 响应) 应用互易定理时，不仅有量的大小问题，而且还有方 向问题。一般电源的移动方法为：平移法和旋转法。 互易定理用于解平衡电桥电路和对称电路较方便。 互易性与无源性是互不相干的，回转器是无源器件， 但不能互易。 §3.4 互易定理

上游充通大学 3.4互易定理 SHANGHAI JIAO TONG UNIVERSITY 40 8V 022 例 求图示电路中的电流I。 22 12[ 20 解所示为复杂电路，用互易定 理可化简成串并联方法求解 的简单电路。 I1=2A,I2=4/3A,I3=2/3A KCL:=I2-I3=2/3A 此例也说明，同电位不等于 无电流

§3.4 互易定理 例 求图示电路中的电流I。 解 所示为复杂电路，用互易定 理可化简成串并联方法求解 的简单电路。 I1=2A，I2=4/3A，I3=2/3A KCL：I=I2-I3=2/3A 此例也说明，同电位不等于 无电流