《电工技术》课程教学资源（学习资料）电工知识点总结（共八讲）

第一讲电路的基本概念 1·研究电路的一般方法 电路模型是实际电路结构及功能的抽象化表示，是各种理想化元件模型的组合。分析电路的 计算。研究的方法是将电路中的电气设备用理想元件替代，直流电路的理想元件是理想电源( 2.电阻和欧姆定律 在导体中，电荷受电场力作用运动时，总是要受到阻碍，电阻就是表征这一性质的参数，欧 常称特性约束。金属导体的电阻与导体长度和材料的电阻率成正比，与截面积成反比，注意这 导体的电阻还与温度有关，绝大多数金属导体，温度愈高，电阻愈大。与电流大小无关的电阻叫 3·电流、电压、电位及电功率 (1)电荷的有规则的定向运动就形成了电流。电流的大小用电流强度（简称电流）来表示 一般用符号i表示，直流用符号1表示。 (2)电路中a、b两点间电压，其大小等于电场力由a点移动单位正电荷到b点所作的 (V),电压一般用符号“ab表示，直流电压用符号U表示。电路中某点到参考点之间的 (3)电流和电压的参考方向是电路中的一个重要的概念。分析和计算电路时，必须首先说 须在电路图上标出参考方向，参考方向可以任意选定，但一经选定，在电路的分析和计算过程中 (4)电功率是指电能量对时间的变化率，用符号p或P表示，SI单位是瓦[特]( 表示电路提供功率。 4,元件的约束 电路元件的伏安关系（特性方程）称为元件约束。在电压、电流取关联参考方向下，有： (1)电阻元件的特性方程为

第一讲 电路的基本概念 1 ．研究电路的一般方法 电路模型是实际电路结构及功能的抽象化表示，是各种理想化元件模型的组合。分析电路的关键是首先建立电路模型，然后再按照电路定律及规律进行分析 计算。 研究的方法是将电路中的电气设备用理想元件替代，直流电路的理想元件是理想电源（电压源或电流源）和电阻，由理想元件构成电路模型。 2 ．电阻和 欧姆定律 在导体中，电荷受电场力作用运动时，总是要受到阻碍，电阻就是表征这一性质的参数，欧姆定律是说明电流、电压、电阻三者之间相互关系的定律， 通 常称特性约束。 金属导体的电阻与导体长度和材料的电阻率成正比，与截面积成反比，注意这里指的是沿电流方向的长度，而截面则是与电流方向相垂直的。 导体的电阻还与温度有关，绝大多数金属导体，温度愈高，电阻愈大。与电流大小无关的电阻叫线性电阻。由线性电阻和电源构成的电路叫线性电阻性电路 3 ．电流、电压、电位及电功率 （ 1 ）电荷的有规则的定向运动就形成了电流。电流的大小用电流强度（简称电流）来表示；其方向指正电荷运动的方向。 SI 单位是安培（ A ），电流 一般用符号 i 表示，直流用符号 I 表示。 （ 2 ）电路中 a 、b 两点间电压，其大小等于电场力由 a 点移动单位正电荷到 b 点所作的功；其方向是由高电位点 指向低 电位点。SI 单位是伏 [ 特 ] （ V ），电压一般用符号 u ab 表示，直流电压用符号 U 表示。 电路中某点到参考点之间的电压就是该点的电位，其计算方法与计算电压相同。 （ 3 ）电流和电压的参考方向是电路中的一个重要的概念。分析和计算电路时， 必须首先设定电流和电压的参考方向，这样计算的结果才有实际意义。 必 须在电路图上标出参考方向，参考方向可以任意选定，但一经选定，在电路的分析和计算过程中则不能改变。通常选取电压和电流的参考方向为关联参考方向。 （ 4 ）电功率是指电能量对时间的变化率，用符号 p 或 P 表示， SI 单位是瓦 [ 特 ] （ W ）。 在关联参考方向下， P>0 ，表示电路消耗功率； P<0 ， 表示电路提供功率。 4 ．元件的约束 电路元件的伏安关系（特性方程）称为元件约束。在电压、电流取关联参考方向下，有： （ 1 ）电阻元件的特性方程为

“=及，直流电路中U= (2)电压源的特性方程 “=“,直流电路中0= (3)电流源的特性方程 1s,直流电路中1=s 5·电压源和电流源 电路中的供能元件称为电源，可以采用两种模型表示，即电压源与电流源。 (1)对理想电压源和理想电流源必须分别建立恒压和恒流的概念。 (2）理想电压源和理想电流源实际上并不存在，只是抽象出来的一种元件模型。但理想 条件。 (3)理想电压源的输出电压和理想电流源的输出电流是由它们自身确定的值，与外电路 有关。而理想电流源的电动势或端电压有电流无关，与外电路情况有关。 注意凡与理想电压源并联的元件，其两端电压均等于理想电压源：凡与理想电流源串联的入 可合并成一个等效的理想电压源：多个理想电流源并联时，可合并成一个等效的理想电流源： (4)实际电压源具有内阻，可用理想电压源与一电阻串联的组合模型表示。实际电流沙 示，实际电流源不允许开路。电压源、电流源两者等效变换的条件：女：”收或。=心，两 电压源、电流源的等效变换可简化电路。 6,基尔霍夫定律 基尔霍夫定律是电路的基本定律，是本章的重点之一。它具有普遍的适用性，适用于由各利 尔霍夫定律是研究电路结构的基本定律。它包括基尔霍夫电流定律和基尔霍夫电压定律

，直流电路中 （ 2 ）电压源的特性方程 ，直流电路中 （ 3 ）电流源的特性方程 ，直流电路中 5 ．电压源和电流源 电路中的供能元件称为电源，可以采用两种模型表示，即电压源与电流源。 （ 1 ）对理想电压源和理想电流源必须分别建立恒压和恒流的概念。 （ 2 ）理想电压源和理想电流源实际上并不存在，只是抽象出来的一种元件模型。但理想电压源和理想电流源间不能等效，因为他们无法满足对外等效的 条件。 （ 3 ）理想电压源的输出电压和理想电流源的输出电流是由它们自身确定的值，与外电路无关，理想电压源的电流与电动势或端电压无关，与外电路情况 有关。而理想电流源的电动势或端电压有电流无关，与外电路情况有关。 注意凡与理想电压源并联的元件，其两端电压均等于理想电压源；凡与理想电流源串联的元件，其电流均等于理想电流源的电流。几个理想电压源串联时， 可合并成一个等效的理想电压源；多个理想电流源并联时，可合并成一个等效的理想电流源。 （ 4 ）实际电压源具有内阻，可用理想电压源与 一 电阻串联的组合模型表示。实际电流源有电流在内部流动，可用理想电流源与电阻并联的组合模型表 示，实际电流源不允许开路。电压源、电流源两者等效变换的条件： ， 两者对外特性是一样的，但对电源内部，则是 不 等效的。 运用 电压源、电流源的等效变换可简化电路。 6 ．基尔霍夫定律 基尔霍夫定律是电路的基本定律，是本章的重点之一。它具有普遍的适用性，适用于由各种不同元件构成的电路中任一瞬时，任何波形的电压和电流。 基 尔霍夫定律是研究电路结构的基本定律。它包括基尔霍夫电流定律和基尔霍夫电压定律

(1)基尔霍夫电流定律 基尔霍夫电流定律适用于节点，确定了电路中各支路电流之间的约束关系，反映电流连笺 路电流的代数和等于零，即∑0=0，直流电路中，∑1=0，或∑x=∑。基尔霍夫龙 制约的关系。应用于节点，也可推广应用于包围部分电路中的任一假设的闭合面。 (2)基尔霍夫电压定律(KVL) 基尔霍夫电压定律适用于回路，反映的是电压与路径无关。该定律说明：在任一时刻，沿任 直流电路中，∑)=0。基尔霍夫定律电压定律反映了一个回路中各部分电压间相互制约的关 夫定律列式子时，先要在电路图上标出电流、电压或电动势的正方向。因为式子各项前的正负号 基尔霍夫电流定律和电压定律是电路中两个基本定律，表达的约束关系通常称为拓朴约牙 中参数电路、任何时刻都必须遵循这两条定律。学习时应注意正确理解节点、支路、回路、网孔 第二讲直流电阻电路的分析 “等效”是电路理论中一个非常重要的概念。所谓两个结构和元件参数完全不同的电路 们对外端钮上的电压和电流的关系完全相同。因此将电路中的某一部分用另一种电路结构与元 路中的电压和电流。据此便可推出各种电路的等效变换关系，从而极大地方便了电路。 1·电阻串并联等效变换 (1)电阻的串联： ·通过各电阻的电流相同，同为I。 ·总电压等于各电阻分电压之和。即可=可+U,+可3。 ·几个电阻串联的电路，可以用一个等效电阻R替代。R=R+R,+R:

（ 1 ）基尔霍夫电流定律 基尔霍夫电流定律适用于节点， 确定了电路中各支路电流之间的约束关系， 反映电流连续性原理， 该定律说明：在任一时刻，流出任 一 节点的所有支 路电流的代数和等于零，即 ，直流电路中， ，或 。 基尔霍夫定律电流定律反映了汇合到电路中任一节点的各支路电流间相互 制约的关系。应用于节点，也可推广应用于包围部分电路中的任一假设的闭合面。 （ 2 ）基尔霍夫电压定律 （ KVL ） 基尔霍夫电压定律适用于回路，反映的是电压与路径无关。该定律说明：在任一时刻，沿任一回路 的所有支路或元件的电压代数和等于零，即 ， 直流电路中， 。 基尔霍夫定律电压定律反映了一个回路中各部分电压间相互制约的关系。应用于闭合回路，也可应用于回路的部分电路。应用基尔霍 夫定律列式子时，先要在电路图上标出电流、电压或电动势的正方向。因为式子各项前的正负号是由它们的正方向确定的。 基尔霍夫电流定律和电压定律是电路中两个基本定律， 表达的约束关系通常称为 拓朴 约束。 它们只取决与电路的连接方式，与元件的性质无关。任何集 中参数电路、任何时刻都必须遵循这两条定律。学习时应注意正确理解节点、支路、回路、网孔的定义。 第二讲 直流电阻电路的分析 “ 等效 ” 是电路理论中一个非常重要的概念。 所谓两个结构和元件参数完全不同的电路 “ 等效 ” ， 是指它们对外电路的作用效果完全相同， 即它 们对外端钮上的电压和电流的关系完全相同。 因此将电路中的某一部分用另一种电路结构与元件参数代替后， 不会影响原电路中留下来末作变换的任何一条支 路中的电压和电流。 据此便可推出各种电路的等效变换关系， 从而极大地方便了电路。 1 ．电阻串并联等效变换 （ 1 ）电阻的串联： • 通过各电阻的电流相同，同为 I 。 • 总电压等于各电阻分电压之 和 。即 。 • 几个电阻串联的电路，可以用一个等效电阻 R 替代。

·分压公式： 可=-可，=-受可 R ·功率分配各个电阻上消耗的功率之各等于等效电阻吸收的功率，即：P=B+B+B (2)电阻的并联： (a)各电阻上电压相同： (仙)各分支电流之和等于等效后的电流，即I=山+工，+： 1为 1+1 (@)几个电阻并联后的电路，可以用一个等效电阻R替代，即RRR,R:G= R R2 R2 -I ※特殊：两个电阻并联时， R=k+R, (d)分流公式： U2,U2,02U2 (e)功率分配： P=B+B,+BR十+R,R 负载增加，是指并联的电阻越来越多，R并越小，电源供给的电流和功率增加了。 2.电阻星形联接与三角形联接的等效变换 无源二端网络是整个网络的一部分，有两个端钮与电路的其余部分连接，它的内部没有电源， 有两个以上电源的电路称为复杂电路，有时可以将其中一部分用△一Y变换后计算。Y一△

• 分压公式： ； 。 • 功率分配：各个电阻上消耗的功率之各等于等效电阻吸收的功率，即： （ 2 ）电阻的并联： (a) 各电阻上电压相同； (b) 各分支电流之和等于等效后的电流，即 ； (c) 几个电阻并联后的电路，可以用一个等效电阻 R 替代，即 ； 。 ※特殊：两个电阻并联时， ， ， (d) 分流公式： ， (e) 功率分配： 负载增加，是指并联的电阻越来越多， R 并 越小，电源供给的电流和功率增加了。 2 ．电阻星形联接与三角形联接的等效变换 无源二端网络是整个网络的一部分，有两个端钮与电路的其余部分连接，它的内部没有电源，总可以简化为一个等效电阻。一般不能用电阻串并联法化简含 有两个以上电源的电路称为复杂电路，有时可以将其中一部分用 Δ— Y 变换后计算。 Y —Δ 互相转换，必须遵从等效原则

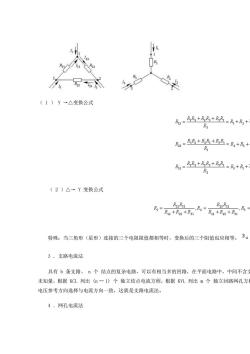
(1)Y→△变换公式 R3 R=8B+品8+民8=R+R十 及1=品+品8+品8=R+R+ K2 (2)△→Y变换公式 R2R31 R23R2 +品+ , 特殊：当三角形（星形）连接的三个电阻阻值都相等时，变换后的三个阻值也应相等。R4 3,支路电流法 具有b条支路、个结点的复杂电路，可以有相当多的回路，在平面电路中，中间不含 未知量，根据KCL列出（一）个独立结点电流方程，根据KVL列出m个独立回路网孔方 电压参考方向选择与电流方向一致，这就是支路电流法。 4·网孔电流法

（ 1 ） Y →△变换公式 （ 2 ）△→ Y 变换公式 特殊：当三角形（星形）连接的三个电阻阻值都相等时，变换后的三个阻值也应相等。 ， 。 3 ．支路电流法 具有 b 条支路、 n 个 结点的复杂电路，可以有相当多的回路，在平面电路中，中间不含支路的回路称为网孔，网孔数 m=b — (n — 1) 。用支路电流作 未知量，根据 KCL 列出 (n — 1) 个 独立结点电流方程，根据 KVL 列出 m 个 独立回路网孔方程，正好求解 b 条支路电流。支路电流参考方向是任意假设的， 电压参考方向选择与电流方向一致，这就是支路电流法。 4 ．网孔电流法

假想的网孔电流，自动满足KCL,应用KL建立m个网孔方程，解出网孔电流后，再求 与本网孔有关的所有电阻之和是自电阻，与相邻网孔关联的电阻称为互电阻。所有网孔电流的查 5,结点电压法 用假设结点j对参考结点0的电压Uj0作未知量，使之自动满足KVL,则只需应用KC 电流，也能使计算简化。这就是结点电压法。列结点方程时，所有与该点连接的支路电导之和称为 支路电流法、网孔电流法和结点电压法都是应用基尔霍夫两条定律进行分析计算的。通常网 6.叠加定理 叠加定理是线性电路的重要原理，从数学上看，叠加定理就是线性方程的可加性。所以叠 电流可看作由各个电源单独作用时在该支路所产生的电压、电流的代数和。由支路电流法和节点 分解为许多较简单的电路，从而使电路分析过程大大简化。叠加定理的重要性不在于应用它来 的非正弦交流电路、暂态过程以及电子电路的分析中也都起较重要的作用。 运用叠加原理时应注意以下问题： (1)只适用于线性电路： (2）某一电源作用时，其他电源中理想电压源短路，理想电流源开路，电路其余部分 (3)最后叠加时，结果为”代数和”，即要注意各个电源单独作用时的电流和电 (4)叠加原理只适用于电压和电流，不适用于功率。 7,戴维宁定理 戴维宁定理指出：任何一个线性有源电阻性二端网络，对外电路来说，可以用一个电压源 网络用一个电压源来等效代替，从而使电路的分析和计算得到简化。此法尤其适用于求解复杂 源二段网络，可以等效为电压源，这样可以将复杂电路化简成简单电路，方便的求出待求的量 路电流或电压。解题过程可分为如下三个步骤进行。 (1)求开路电压：

假想的网孔电流，自动满足 KCL ，应用 KVL 建立 m 个 网孔方程，解出网孔电流后，再求支路电流，使计算简化，这就是网孔电流法。列网孔电压方程时 与本网孔有关的所有电阻之和是自电阻，与相邻网孔关联的电阻称为互电阻。所有网孔电流的参考方向，一般选择顺时针方向，因此互电阻恒为负值。 5 ．结点电压法 用假设结点 j 对参考结点 0 的电压 U jo 作未知量，使之自动满足 KVL ，则只需应用 KCL 列（ n-1 ） 个 结点电压方程，解出结点电压后再求各支路 电流，也能使计算简化。这就是结点电压法。列结点方程时，所有与该点连接的支路电导之和称为自电导，与相邻结点关联的支路电导是互导，互电导恒为负值。 支路电流法、网孔电流法和结点电压法都是应用基尔霍夫两条定律进行分析计算的。通常网络结构 (n — 1) ≤ m ，所以结点电压法的应用更为广泛。 6 ．叠加定理 叠加定理是线性电路的重要原理 , 从数学上看 , 叠加定理就是线性方程的可加性。所以叠加定理适用于线性电路的电压、电流的计算。即各支路的电压、 电流可看作由各个电源单独作用时在该支路所产生的电压、电流的代数和。由支路电流法和节点电压法得出的都是线性代数方程。利用叠加原理可以将复杂电路 分解为许多较简单的电路 , 从而使电路分析过程大大简化。叠加定理的重要性不在于应用它来计算复杂电路 , 而在于它是分析线性电路的普遍原理 , 在后面 的非正弦交流电路、暂态过程以及电子电路的分析中也都起较重要的作用。 运用叠加原理时应注意以下问题 : （ 1 ）只适用于线性电路； （ 2 ）某一电源作用时 , 其他电源中理想电压源短路 , 理想电流源开路 , 电路其余部分不变； （ 3 ） 最后叠加时 , 结果为 ” 代数和 ” , 即要注意各个电源单独作用时的电流和电压分量的参考方向是否与总电流和电压的参考方向一致； （ 4 ）叠加原理只适用于电压和电流 , 不适用于功率。 7 ．戴维宁定理 戴维宁定理指出：任何一个线性有源电阻性二端网络，对外电路来说，可以用一个电压源与一个电阻串联的支路等效代替。戴维宁 定理将复杂的有源二端 网络用一个电压源来等效代替 , 从而使电路的分析和计算得到简化。此法尤其适用于求解复杂电路中某一支路的电流 , 只要 将带求支路 划出 , 剩下 一 有 源二段网络 , 可以等效为电压源 , 这样可以将复杂电路化简成简单电路，方便的求出待求的量。 戴维宁定理特别适用于求解线性有源电阻性二端网络的某支 路电流或电压。解题过程可分为如下三个步骤进行。 （ 1 ）求开路电压；

(2)求等效电阻，电路中的电压源短路，电流源开路： (3)作出戴维宁等效电路，计算所求支路的电流或电压。 运用戴维宁定理时应注意 (1)等效是对有源二端网络外部而言的： (2)求有源二端网络的开路电压或短路电流时应先分析一下网络的情况。若为简单电路， 则还需利用其他解复杂电路的方法（如支路电流法，节点电压法，以及叠加原理等）才能 (3)求等效电压源内阻的方法有：开路电压与短路电流之比以及除源等效法，一般 (4)待求支路可以是无源支路，也可以是有源支路。 第三讲电容与电感 1·电场的基本知识 带电体周围存在有电场，电荷放在电场中受电场力。表明电场强弱的物理量是电场强度矢量 它的电场容易计算。其他任何带电体的电场都可用分布在带电体上的电荷元的电场强度矢量合 可以用电力线和等位面来描绘。 电介质的极化产生一个与外电场相反的附加电场，削弱外电场。在介质中电场强度E比在 电位移和电场强度都是表征电场强度的物理量，D与介质无关，E与e成反比，D=ε 电介质是不导电的，是电工技术中必不可少的绝缘物。但在强电场中会被击穿，破坏绝缘性 和设法使电场分布均匀等措施。 2·电容 电容是表征两导体在单位电压作用下储存电荷的能力，只与导体形状尺寸以及中间介质有关

（ 2 ）求等效电阻，电路中的电压源短路，电流源开路； （ 3 ） 作出 戴维宁等效电路，计算所求支路的电流或电压。 运用 戴维宁 定理时应注意： （ 1 ）等效是对有源二端网络外部而言的； （ 2 ）求有源二端网络的开路电压或短路电流时应先分析一下网络的情况。若为简单电路 , 只需利用欧姆定理和基尔霍夫定理便可求解；若为复杂电路 , 则还需利用其他 解复杂 电路的方法 ( 如支路电流法 , 节点电压法 , 以及叠加原理等 ) 才能求出。 （ 3 ） 求等效电压源内阻的方法有 : 开路电压与短路电流之比 以及除源等 效法 , 一般来说 , 后者较简单。 （ 4 ）待求支路可以是无源支路 , 也可以是有源支路。 第三讲 电容与电感 1 ．电场的基本知识 带电体周围存在有电场，电荷放在电场中受电场力。表明电场强弱的物理量是电场强度矢量，它等于单位正电荷受到的电场力。虽然点电荷是理想状态，但 它的电场容易计算。其他任何带电体的电场都可用分布在带电体上的 电荷元 的电场强度矢量合成求出。由此求出两平面中间的电场强度为 E= σ / ε。电场 可以用电力线和等位面来描绘。 电介质的极化产生一个与外电场相反的附加电场，削弱外电场。在介质中电场强度 E 比在真空中 E 0 小 ε r 倍 ，ε r 是相对介电常数。 电位移和电场强度都是表征电场强度的物理量， D 与介质无关， E 与 ε 成反比， D= εΕ。 电介质是不导电的，是电工技术中必不可少的绝缘物。但在强电场中会被击穿，破坏绝缘性能。为了安全用电防止击穿，要采取选择好的材料，加厚绝缘层 和设法使电场分布均匀等措施。 2 ．电容 电容是表征两导体在单位电压作用下储存电荷的能力，只与导体形状尺寸以及中间介质有关。平板电容器的电容量为 C ＝ε A/d

几个电容器进行串联，并联或串并联时可用一个等效电容替代。 注意几个电容器串联之后，等效电容小于其中任一电容。而并联后的等效电容为各电容之 电容器是储能元件，充放电过程是能量储存和释放过程。电容器的充放电都需一段时间，才 3。磁场基本知识 运动电荷和载流导线周围存在有磁场。表征磁场强度的物理量是磁感应强度（矢量）B，月 运动电荷在磁场中受力为下=QvB(v上B),截流直导体受磁场力F=B【I(t⊥B 力。 运动电荷的磁感应强度B=μQD/2Πr2，方向由右手螺旋定则确定。 磁场强度H与磁感应强度B都是表征磁场强弱的物理量，都是矢量。前者与介质无关，后 磁介质有三种，顺磁质和反磁质的μ都与真空中40相差不大，μ≈0，r≈ 在磁场中取任意封闭面，∮A BdAcos B=0，穿人封闭面的磁通等于穿出磁通，磁通元 在磁场中，取一任意封闭路径，9d1c0sB=∑，这一安培环路定律是确定 导体在磁场中作切割磁感线运动，产生感应电动势。=B【·,方向用右手定则确定。 ·电感 线圈中磁链发生变化时，线圈产生感应电动势e=-d平/t。负号表示建立电动势过程中 产生磁感应电动势的过程实质是电场建立过程。因此：(1)导体（含自由电荷）在磁场 也建立电场。 电流周围存在磁场，与线圈交链的磁通链平与电流的比值称为电感 变化的电流产生变化的磁场，线圈的自感电动势与电流变化率成正比

几个电容器进行串联，并联或串并联时可用一个等效电容替代。 注意几个电容器串联之后，等效电容小于其中任 一 电容。而并联后的等效电容为各电容之 和 。需要大的电容时，可用几个电容并联。 电容器是储能元件，充放电过程是能量储存和释放过程。电容器的充放电都需一段时间，才能从一种状态变化到新的状态。 3 ．磁场基本知识 运动电荷和载流导线周围存在有磁场。表征磁场强度的物理量是磁感应强度（矢量） B ，用单位正电荷以单位速度运动受到最大磁场力来表示。 运动电荷在磁场中受力为 F ＝ Q υ B( υ⊥ B) ，截流直导体受磁场力 F=B ι I( ι⊥ B), 方向由左手定则确定，注意只限制在磁场内的载流导体才受 力。 运动电荷的磁感应强度 B ＝μ Q υ /2 л r 2 ，方向由右手螺旋定则确定。 磁场强度 H 与磁感应强度 B 都是表征磁场强弱的物理量，都是矢量。前者与介质无关，后者与磁导率 μ 成正比， B ＝μ H 。 磁介质有三种，顺磁质 和反磁质 的 μ 都与真空中 μ 0 相差不大，μ≈μ 0 ，μ r ≈ 1 ，铁磁质 μ 很大，不是常数，磁化后有剩磁存在。 在磁场中取任意封闭面，∮ A BdAcos β＝ 0 ，穿人封闭面的磁通等于穿出磁通，磁通元始无终。 在磁场中，取 一 任意封闭路径，∮ ι Hd ι cos β＝ ，这一安培环路定律是确定磁场 H 与电流 I 的关系重要定律。 导体在磁场中作切割磁感线运动，产生感应电动势 e ＝ Bιυ ，方向用右手定则确定。 • 电感 线圈中磁链发生变化时，线圈产生感应电动势 e ＝ - dΨ/dt 。负号表示建立电动势过程中，电荷的运动总是阻碍磁场变化的。方向用右手螺旋法则确定。 产生磁感应电动势的过程实质是电场建立过程。因此：（ 1 ）导体（含自由电荷）在磁场中切割磁力线时，导体中建立电场；（ 2 ）变动的磁场在导体中 也建立电场。 电流周围存在磁场，与线圈交链的磁通链 Ψ 与电流的比值称为电感。 变化的电流产生变化的磁场，线圈的自感电动势与电流变化率成正比

电感只与线圈匝数、几何尺寸和介质有关，除铁磁介质外，电感是常数，与电流无关。 两线圈之间有互感。线圈1的电流产生的磁通有部分与线圈2交链，叫磁耦合，耦合系素 电感线圈是储能元件，通过的电流不能突变 电感线圈（与电阻串联）与直流电源接通时，电流由零过渡到新的稳态UsR，储存能量 电感线圈与电源断开时，能量释放。 4·注意 静止的电荷周围存在电场，运动的电荷周围也有电场，而且还有磁场。因此，运动的电荷、 另一方面，电荷放在电场中要受电场力，下=Q,运动的电荷不仅受电场力，放在磁场 体在磁场中受力)。电场强度E、磁感应强度B就是用电荷受力定义的，都是矢量，要弄清方 第三，当磁场磁感线变化（或者是切割导体）时，会产生感应电动势，这是电场磁场的又 电工中用的材料对电路而言有导体和绝缘体，后者对电场而言称为电介质，在电场中会被极 性能的，在介质中，E与e成反比，￡总是大于真空的e0。在磁场中，所有材料都是磁介 原磁场外，其余材料磁化后有的削弱、有的增强原磁场，但都影响不大。磁导率“是表征这一性 一般μ≈μ0。而电位移D和磁场强度的H,都与介质无关。 安全用电是重要的，在强电场作用下，绝缘会被击穿，仅选择优良的材料，加大厚度是不 本章研究了各种带电导体的电场和载流导体的磁场。特别带正负电荷的两平行平板的电场几 Q/八。环形螺管线圈，磁场几乎全部集中在线圈内，也近似均匀的，可求电感L=平1，显名 和电感线圈，C和L较大，是电路中重要的元件。 为了研究方便，从静电场开始，简单介绍了恒定电场。最后对电容器充放电过程有初步了解。 变化的，电场的性质，例如两极板电压μ等于电场强度与距离d的乘积，电场强度与e成反H 同理，开始讨论的是恒定磁场，但电感线圈与直流电源接通后，电流是变化的，磁场也是变

电感只与线圈匝数、几何尺寸和介质有关，除铁磁介质外，电感是常数，与电流无关。 两线圈之间有互感。线圈 1 的电流产生的磁通有部分与线圈 2 交链，叫磁耦合， 耦合系款一般 小于 1 ，最大等于 1 。 电感线圈是储能元件，通过的电流不能突变。 电感线圈（与电阻串联）与直流电源接通时，电流由零过渡到新的稳态 U s /R ，储存能量 LI 2 。 电感线圈与电源断开时，能量释放。 4 ．注意 静止的电荷周围存在电场，运动的电荷周围也有电场，而且还有磁场。因此，运动的电荷、电场和磁场，三者是统一存在，相互关联的一个整体。 另一方面，电荷放在电场中要受电场力， F ＝ QE ，运动的电荷不仅受电场力，放在磁场中，还要受磁场力 F ＝ QυB 或 F ＝ B ι I （适用于载流导 体在磁场中受力）。电场强度 E 、磁感应强度 B 就是用电荷受力定义的，都是矢量，要弄清方向是如何确定的。 第三，当磁场磁感线变化（或者是切割导体）时，会产生感应电动势，这是电场磁场的又一种关联，也是电荷、电场、磁场之间的联系。 电工中用的材料对电路而言有导体和绝缘体，后者对电场而言称为电介质，在电场中会被极化，产生附加电场，削弱原电场， 介 电系数 ε 就是表征这一 性能的，在介质中， E 与 ε 成反比，ε 总是大于真空的 ε 0 。在磁场中，所有材料都是磁介质，在磁场中会被磁化，产生附加磁场，除了铁磁材料大大增强 原磁场外，其余材料磁化后有的削弱、有的增强原磁场，但都影响不大。磁导率 μ 是表征这一性能的。在介质中 B 与 μ 成正比，除了铁磁材料的 μ 》 μ 0 ， 一般 μ≈μ 0 。而电位移 D 和磁场强度的 H ，都与介质无关。 安全用电是重要的，在强电场作用下， 绝缘会 被击穿，仅选择优良的材料，加大厚度是不够的，还要使电场分布合理。 本章研究了各种带电导体的电场和载流导体的磁场。特别带正负电荷的两平行平板的电场几乎全部集中在平板之间，而且是均匀的，从而可求电容 C ＝ Q/U 。环形螺管线圈，磁场几乎全部集中在线圈内，也近似均匀的，可求电感 L ＝ Ψ/I ，显然，任何导体之间会有电容，单根导体也有电感，但平板电容器 和电感线圈， C 和 L 较大，是电路中重要的元件。 为了研究方便，从静电场开始，简单介绍了恒定电场。最后对电容器充放电过程有初步了解。已充电到稳态的电场是静电场，在充电或放电过程中，电场是 变化的，电场的性质，例如两极板电压 μ 等于电场强度与距离 d 的乘积，电场强度与 ε 成反比等等，与静电场一样。 同理，开始讨论的是恒定磁场，但电感线圈与直流电源接通后，电流是变化的，磁场也是变化的，有感应电动势产生，稳定之后，磁场才是恒定的。磁场的

基本性质，对变化磁场仍然适用。 四讲正弦交流电路的分析 1·正弦交流电的基本概念 输出正弦交流电压的理想电压源是正弦交流电源，一般交流电源是交流发电机和电子振荡器 正弦交流电i=1m(+网)可由最大值l、角频率0（或频率f或周期T, 初始时刻的大小和变化进程。振幅、频率、初相三者是正弦量的三要素。振幅即正弦量的最大值 有1人反的关系。频率是衡量正弦量变化快慢的量，等于每秒完成的循环周数。初相是 向有关。 两个同频率正弦量的相位差等于其初相之差，实质上反映了时间差，它与计时起点无关。所 进程的比较。不同频率的两个正弦量无从比较。 2.正弦交流电的表示法 正弦交流电可用解析式、波形图和相量图（相量复数式）三种方法来表示。三者之间可以 正弦量的旋转矢量是复指数函数，它与正弦函数的关系是i(t)=I m sina(ot+中)=lm 工技术中常采用相量的复数运算与作相量图相结合的方法分析正弦电路。解析式和波形图是正弦 析式及波形图，而是借助正弦量的相量。因此三种表示形式相互对应的关系要熟记。参考正弦量 参考相量为基准，朝逆时针方向旋转的幅角为正值，反之为负值。 例：某电流正弦量，表示方法如下： ①三角函数式（瞬时表达式或解析式）： i1=6sin(314t-30。)A

基本性质，对变化磁场仍然适用。 四讲 正弦交流电路的分析 1 ．正弦交流电的基本概念 输出正弦交流电压的理想电压源是正弦交流电源，一般交流电源是交流发电机和电子振荡器。 正弦交流电 可由最大值 、角频率 （或频率 f 或周期 T ， ， ）和初相位 来描述它的大小、变化快慢及 时 初始时刻的大小和变化进程。 振幅、频率、初相三者是正弦量的三要素。振幅即正弦量的最大值，是衡量正弦量大小的量， 正弦交流电的有效值与最大值之间 有 的关系。 频率是衡量正弦量变化快慢的量，等于每秒完成的循环周数。初相是 t ＝ 0 时的相位，不仅与计时起点有关，而且与正弦量参考方 向有关。 两个同频率正弦量的相位差等于其初相之差，实质上反映了时间差，它与计时起点无关。所谓超前、滞后、同相、反相和正交，都是两个同频率正弦量变化 进程的比较。不同频率的两个正弦量无从比较。 2 ．正弦交流电的表示法 正弦交流电可用解析式、波形图和相量图（相量复数式）三种方法来表示。 三者之间可以互相转换。 正弦量的旋转矢量是复指数函数，它与正弦函数的关系是 ì (t)=I m sina( ω t+ Φ )=lm[I m e j( ω t+ ф ) ] ，它是正弦电路分析的重要工具。电 工技术中常采用相量的复数运算与作相量图相结合的方法分析正弦电路。解析式和波形图是正弦量最基本的表示形式，在正弦电路分析中不直接求解正弦量的解 析式及波形图，而是借助正弦量的相量。因此三种表示形式相互对应的关系要熟记。参考正弦量的相量称为参考相量，在同一个相量图上只有一个参考相量，以 参考相量为基准，朝逆时针方向旋转的幅角为正值，反之为负值。 例：某电流正弦量，表示方法如下： ①三角函数式（瞬时表达式或解析式）： i 1 ＝ 6sin （ 314t － 30 °） A