《养分资源管理》课程教学课件（PPT讲稿）第二章 基本原理与基本方法 第一节 养分资源管理的基本原理 第二节 肥料效应函数在养分资源管理中的应用

第二章 养分资源管理的基本原理与基本方法 第一节养分资源管理的基本原理 第二节肥料效应函数在养分资源管理中的应用

第一节 养分资源管理的基本原理 第二节 肥料效应函数在养分资源管理中的应用 第二章 养分资源管理的基本原理与基本方法

y=0.09x+81.9x159 R2=0.4939 R2=0.185 120 800 100 600 60 ● 400 40 200 20 0 100 200 300 400 500 氮肥用量(kgN/ha) 玉米产量和氨素损失与施氮量的关系 (Cui et al,unpublished

y = 0.09x + 81.9 x159 R 2 = 0.185 y = 22.599e0.007x R 2 = 0.4939 0 20 40 60 80 100 120 0 100 200 300 400 500 氮肥用量(kg N/ha) 相对产量(%) 0 200 400 600 800 氮素损失(kg N/ha) (Cui et al, unpublished ) 玉米产量和氮素损失与施氮量的关系

一、肥料效应函数的概念与作用 肥料效应：作物产量对施肥的反应。 肥料效应函数：也叫肥料效应方程、施肥模型， 指表达作物产量对施肥反应的数学函数式

一、肥料效应函数的概念与作用 肥料效应：作物产量对施肥的反应。 肥料效应函数：也叫肥料效应方程、施肥模型， 指表达作物产量对施肥反应的数学函数式

肥料效应函数的作用：可以判断肥料养分效应的大 小和特征，进行肥料新品种的评价；可以确定最佳 施肥量、最大施肥量等。 肥料效应函数的代数形式及其系数值取决于土壤、 作物、肥料种类及栽培技术条件等多种因素

肥料效应函数的作用：可以判断肥料养分效应的大 小和特征，进行肥料新品种的评价；可以确定最佳 施肥量、最大施肥量等。 肥料效应函数的代数形式及其系数值取决于土壤、 作物、肥料种类及栽培技术条件等多种因素

二、肥料效应函数的类型与特征 肥料效应方程式从数学形式上分为直线、指数、多项式、 相交直线方程式等，从自变量数上分为一元、多元等。 1、一元肥料效应回归方程式 一元肥料效应方程式有： (1)直线方程式 (2)指数（或对数）方程式 (3)多项式 (4)两条或三条相交直线的效应方程式

二、肥料效应函数的类型与特征 肥料效应方程式从数学形式上分为直线、指数、多项式、 相交直线方程式等，从自变量数上分为一元、多元等。 1、一元肥料效应回归方程式 一元肥料效应方程式有： （1）直线方程式 （2）指数(或对数)方程式 （3）多项式 （4）两条或三条相交直线的效应方程式

(1)直线方程式 y=bo+bix y:产量，bo:施肥前产量水平，b系数 特征：固定报酬，因而该式不能反映当施肥量递 增时表现出的肥效递减现象以及过量施肥，特别 是过量施用N肥时的总产量下降现象。 存在条件：在较低生产水平、较低肥力、施用低 量肥料时，可能符合直线方程

（1）直线方程式 y=b0+b1x y：产量，b0：施肥前产量水平，b1系数 特征：固定报酬，因而该式不能反映当施肥量递 增时表现出的肥效递减现象以及过量施肥，特别 是过量施用N肥时的总产量下降现象。 存在条件：在较低生产水平、较低肥力、施用低 量肥料时，可能符合直线方程

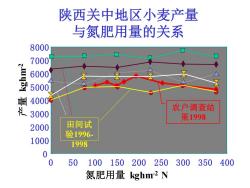
陕西关中地区小麦产量 与氮肥用量的关系 8000 7000 6000 5000 响4000 农户调查结 3000 果1998 2000 田间试 验1996- 1000 1998 0 0 50 100150200 250300350400 氮肥用量kghm2N

陕西关中地区小麦产量 与氮肥用量的关系 0 1000 2000 3000 4000 5000 6000 7000 8000 0 50 100 150 200 250 300 350 400 氮肥用量 kghm-2 N 产量 kghm- 2 农户调查结 果1998 田间试 验1996- 1998

(2)指数（或对数）方程式 1米采利希方程式 由米氏于1909年提出： 对数式为： 1g(A-y)=1gA-cx 指数式为： y=A(1-10-cx) A为增施某一养分可以达到的最高产量，y为养分为x时的实 际产量，C为效应系数。C值愈大，达到一定产量需要的施 肥量愈少，肥料的增产效应愈高

（2）指数(或对数)方程式 i 米采利希方程式 由米氏于1909年提出： 对数式为： lg(A-y)=lgA-cx 指数式为： y=A(1-10-cx) A为增施某一养分可以达到的最高产量，y为养分为x时的实 际产量，C为效应系数。 C值愈大，达到一定产量需要的施 肥量愈少，肥料的增产效应愈高

ii典型的指数方程式 米氏方程中X为养分供应量，包括了土壤养分，不能直 观表达施肥量的影响，为此，克劳斯等提出了修正式，并称 之为典型的指数方程式。 y=yo+d(1-10-cx) yo为不施肥产量 d为最大产量 k为效应系数 iii斯皮尔曼(Spillman)方程式 y=A(1-Rx)

ii典型的指数方程式 米氏方程中X为养分供应量，包括了土壤养分，不能直 观表达施肥量的影响，为此，克劳斯等提出了修正式，并称 之为典型的指数方程式。 y=y0+d(1-10-cx) y0为不施肥产量 d为最大产量 k为效应系数 iii斯皮尔曼(Spillman)方程式 y=A(1-R x)

指数方程式特征：①报酬递减 ②反映最高产量以前的效应 指数方程式都存在一个共同的缺点，即肥料用量没 有超过最高产量施肥量，它们不能反映总产量因施 肥量增加而下降的那部分效应关系

指数方程式特征：①报酬递减 ②反映最高产量以前的效应 指数方程式都存在一个共同的缺点，即肥料用量没 有超过最高产量施肥量，它们不能反映总产量因施 肥量增加而下降的那部分效应关系