《画法几何与工程制图》课程教学资源（教材讲义）第03章 曲线曲面

第5章曲线与曲面 曲线与曲面也是物体表面的重要组成部分。本章讨论常见的曲线、曲面的投影性质与作 图方法。 5.1曲线的形成与投影 1.曲线的形成与分类曲线可以看作为点连续运动的轨迹，也可认为是平面与曲面或两 曲面相交而成。 若曲线上所有的点属于同一平面，则此曲线称为平面曲线，如圆、椭圆、双曲线、抛物 线、渐伸线、摆线等。 若曲线上任意四个连续的点不属于同一平面，则此曲线称为空间曲线，如螺旋线等。 如图5-1所示，过曲线上点B作割线BD,当点D无限趋近于点B时，割线的极限位置 变为BN,即称BN为曲线在点B处的切线。对于平面曲线过切点且垂直于切线的直线，称为 过该点的法线。 图5-1空间曲线及其投影 图5-2不光滑空间曲线 如果曲线在其各点处都具有连续改变的切线，则称该曲线为光滑的曲线。 如图5-2所示的曲线就不是光滑的，因为在点B处切线不能连续变化。 可以用代数方程表示的曲线称为代数曲线。其代数方程的次数就是曲线的次数。对于平 面代数曲线的次数，可以用直线与该曲线最大可能交点数来确定。例如，二次曲线椭圆与直 线就有两个交点。 2.曲线投影的画法一般情况下，曲线至少需要两个投影才能确定出它在空间的形状和 位置。曲线的投影作图，就是按曲线形成的方法，依次画出曲线上一系列的点的各面投影， 然后把各点的同面投影顺次、光滑地连成曲线，这种作图方法称为坐标描点法。为了确保曲 线投影的准确和清晰，应优先选择一些具有关键位置的点，称为特殊点，如极限位置的点（最 高、最低、最前、最后、最左、最右诸点)以及如椭圆长短轴的端点等。 3.曲线投影的基本性质曲线的投影具有以下的性质，根据这些性质，在作曲线投影时， 可以保证投影的正确性和提高投影的准确性。 120

120 第 5 章 曲线与曲面 曲线与曲面也是物体表面的重要组成部分。本章讨论常见的曲线、曲面的投影性质与作 图方法。 5.1 曲线的形成与投影 1.曲线的形成与分类 曲线可以看作为点连续运动的轨迹，也可认为是平面与曲面或两 曲面相交而成。 若曲线上所有的点属于同一平面，则此曲线称为平面曲线，如圆、椭圆、双曲线、抛物 线、渐伸线、摆线等。 若曲线上任意四个连续的点不属于同一平面，则此曲线称为空间曲线，如螺旋线等。 如图 5-1 所示，过曲线上点 B 作割线 BD，当点 D 无限趋近于点 B 时，割线的极限位置 变为 BN，即称 BN 为曲线在点 B 处的切线。对于平面曲线过切点且垂直于切线的直线，称为 过该点的法线。 如果曲线在其各点处都具有连续改变的切线，则称该曲线为光滑的曲线。 如图 5-2 所示的曲线就不是光滑的，因为在点 B 处切线不能连续变化。 可以用代数方程表示的曲线称为代数曲线。其代数方程的次数就是曲线的次数。对于平 面代数曲线的次数，可以用直线与该曲线最大可能交点数来确定。例如，二次曲线椭圆与直 线就有两个交点。 2.曲线投影的画法 一般情况下，曲线至少需要两个投影才能确定出它在空间的形状和 位置。曲线的投影作图，就是按曲线形成的方法，依次画出曲线上一系列的点的各面投影， 然后把各点的同面投影顺次、光滑地连成曲线，这种作图方法称为坐标描点法。为了确保曲 线投影的准确和清晰，应优先选择一些具有关键位置的点，称为特殊点，如极限位置的点（最 高、最低、最前、最后、最左、最右诸点）以及如椭圆长短轴的端点等。 3.曲线投影的基本性质 曲线的投影具有以下的性质，根据这些性质，在作曲线投影时， 可以保证投影的正确性和提高投影的准确性。 N C D A B a b c d n H A B E a e b F C f c 图 5-1 空间曲线及其投影 图 5-2 不光滑空间曲线

(1)曲线的投影一般是曲线，只有当平面曲线所在平面平行于投射线时，投影为直线。 在正投影条件下，该平面垂直于投影面时，曲线投影为直线。 (2)曲线上的点的投影必定在曲线的同面投影上，即点与曲线的从属关系不变， (3)一般情况下平面曲线投影的次数不变。即二次曲线的投影仍为二次曲线。 (4)曲线切线的投影仍为曲线投影的切线（图5-3）。 图53平面曲线的投形性质 图54平行投影面的圆的投影 5.1.1圆的投影 圆是最常见的平面曲线，圆的正投影可能有三种情况：当圆所在平面平行于投影面时， 其投影仍为圆。当圆所在平面垂直于投影面时，则其投影为直线。当圆所在平面倾斜于投影 面时，则其投影为椭圆。 下面根据不同情况分别讨论在正投影图中，圆的投影及其作图。 1,圆所在的平面为投影面平行面当圆所在的平面为投影面平行面时，圆在所平行的投 影面上的投影反映该圆的实形。在另一投影面上的投影为直线，线段的长度等于圆的直径（见 图5-4)。 2.圆所在的平面为投影面垂直面当圆所在的平面为投影面垂直面时，圆在所垂直的投 影面上的投影为直线，线段的长度等于直径。在另一投影面上的投影则为椭圆。 )直观图 b)投影图 图5-5投影面垂直面上的圆 121

121 （1）曲线的投影一般是曲线，只有当平面曲线所在平面平行于投射线时，投影为直线。 在正投影条件下，该平面垂直于投影面时，曲线投影为直线。 （2）曲线上的点的投影必定在曲线的同面投影上，即点与曲线的从属关系不变。 （3）一般情况下平面曲线投影的次数不变。即二次曲线的投影仍为二次曲线。 （4）曲线切线的投影仍为曲线投影的切线（图 5-3）。 5.1.1 圆的投影 圆是最常见的平面曲线，圆的正投影可能有三种情况：当圆所在平面平行于投影面时， 其投影仍为圆。当圆所在平面垂直于投影面时，则其投影为直线。当圆所在平面倾斜于投影 面时，则其投影为椭圆。 下面根据不同情况分别讨论在正投影图中，圆的投影及其作图。 1．圆所在的平面为投影面平行面 当圆所在的平面为投影面平行面时，圆在所平行的投 影面上的投影反映该圆的实形。在另一投影面上的投影为直线，线段的长度等于圆的直径（见 图 5-4）。 2．圆所在的平面为投影面垂直面 当圆所在的平面为投影面垂直面时，圆在所垂直的投 影面上的投影为直线，线段的长度等于直径。在另一投影面上的投影则为椭圆。 a b c d e l k A B C D E T t L a o b c d X a b o c d 图 5-3 平面曲线的投影性质 图 5-4 平行投影面的圆的投影 a c b d a b A B C D O X X a c d b a b c d d c o o o o Dcos D 1 2 1 2 1 2 X a）直观图 b）投影图 图 5-5 投影面垂直面上的圆

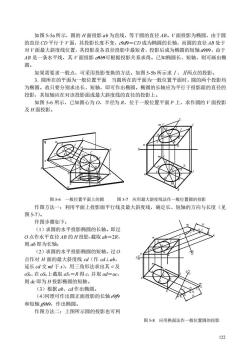
如图55a所示，圆的H面投影ab为直线，等于圆的直径AB。V面投影为椭圆，由于圆 的直径CD平行于V面，其投影长度不变，99=CD成为椭圆的长轴，而圆的直径AB处于 对V面最大斜度线位置，其投影是各直径投影中最短者，投影后成为椭圆的短轴a969,由于 AB是一条水平线，其V面投影9b9可根据投影关系求得。已知椭圆长、短轴，则可画出椭 圆。 如果需要求一般点，可采用投影变换的方法。如图5-5b所示求/、两点的投影。 3.圆所在的平面为一般位置平面当圆所在的平面为一般位置平面时，圆的两个投影均 为椭圆。故只要分别求出长、短轴，即可作出椭圆。椭圆的长轴应为平行于投影面的直径的 投影，其短轴应在对该投影面成最大斜度线的直径的投影上。 如图5-6所示，已知圆心为O,半径为R,位于一般位置平面P上，求作圆的V面投影 及H面投影。 图5-6一般位置平面上的圆 图57应用最大斜度线法作一般位置圆的投影 作图方法一：利用平面上投影面平行线及最大斜度线，确定长、短轴的方向与长度（见 图5-7)。 作图步骤如下： (1)求圆的水平投影椭圆的长轴。即过 O点作水平直径AB的H投影，截取ab=2R, 则ab即为长轴： (2)求圆的水平投影椭圆的短轴。过0 点作对H面的最大斜度线cd(作cd⊥ab, 延长cd交ml于s),用三角形法求出其a及 oS,在oS上截取oS=R得c,并取od=oC, 则dc即为H投影椭圆的短轴。 (3)根据ab、cd作出椭圆 (4)同理可作出圆正面投影的长轴e9/9 和短轴g99,作出椭圆。 作图方法二：上图所示圆的投影也可利 图58应用换面法作一般位置圆的投影 122

122 如图 5-5a 所示，圆的 H 面投影 ab 为直线，等于圆的直径 AB。V 面投影为椭圆，由于圆 的直径 CD 平行于 V 面，其投影长度不变，cd＝CD 成为椭圆的长轴，而圆的直径 AB 处于 对 V 面最大斜度线位置，其投影是各直径投影中最短者，投影后成为椭圆的短轴 ab，由于 AB 是一条水平线，其 V 面投影 ab可根据投影关系求得。已知椭圆长、短轴，则可画出椭 圆。 如果需要求一般点，可采用投影变换的方法。如图 5-5b 所示求Ⅰ、Ⅱ两点的投影。 3．圆所在的平面为一般位置平面 当圆所在的平面为一般位置平面时，圆的两个投影均 为椭圆。故只要分别求出长、短轴，即可作出椭圆。椭圆的长轴应为平行于投影面的直径的 投影，其短轴应在对该投影面成最大斜度线的直径的投影上。 如图 5-6 所示，已知圆心为 O，半径为 R，位于一般位置平面 P 上，求作圆的 V 面投影 及 H 面投影。 作图方法一：利用平面上投影面平行线及最大斜度线，确定长、短轴的方向与长度（见 图 5-7）。 作图步骤如下： （1）求圆的水平投影椭圆的长轴。即过 O 点作水平直径 AB 的 H 投影，截取 ab＝2R， 则 ab 即为长轴； （2）求圆的水平投影椭圆的短轴。过 O 点作对 H 面的最大斜度线 cd（作 cd⊥ab， 延长 cd 交 ml 于 s），用三角形法求出其α及 oS0，在 oS0 上截取 oS1＝R 得 c，并取 od＝oc， 则 dc 即为 H 投影椭圆的短轴。 （3）根据 ab、cd 作出椭圆。 （4）同理可作出圆正面投影的长轴 ef 和短轴 gh，作出椭圆。 作图方法二：上图所示圆的投影也可利 A B C E D F G H L K M N X O a c b d l k m n o m n l k g e h f o H a b c d e f g h l k m n o s X T T S S t m t g f l k b h o a e n 图 5-6 一般位置平面上的圆 图 5-7 应用最大斜度线法作一般位置圆的投影 D n 1 1 1 1 1 1 1 1 1 l m c o a b d n k b o c a d k n m l l k g h f e o m D X X H V X 1V H o1 V 1 H m1 k1 h1 1 g 1 f e1 图 5-8 应用换面法作一般位置圆的投影

用换面法来作出其长短轴（图5-8）。如作圆的水平投影，首先将四边形平面变换成投影面垂 直面，即以V面代替V面，则在V/H体系中圆为垂直面，可根据圆在投量影面垂直面上的作 图方法作出其投影。圆的正面投影也可类似地作出 5.1.2圆柱螺旋线 圆柱螺旋线是工程上应用最广泛的空间曲线。下面讨论其形成及投影作图方法。 b) c 图5-9圆柱螺旋线的形成、投影和展开 1.圆柱螺旋线的形成一动点在正圆柱表面上绕其轴线作等速回转运动，同时沿圆柱的 轴线方向作等速直线运动，则动点在圆柱表面上的轨迹称为圆柱螺旋线。如图5-9妇所示，点 A的轨迹即为圆柱螺旋线。点A旋转一圈沿轴向移动的距离（如A4z)称为导程(P)。当 圆柱的轴线为铅垂线时，从前方垂直向后看，如螺旋线的可见部分为自左向右上升的则称为 右旋螺旋线，反之称为左旋螺旋线。 2.圆柱螺旋线的投影作图方法圆柱直径为d,导程为P的右旋螺旋线，其投影的作图 步骤如下（图5-9b): (1)作出直径为d的圆柱面的两投影，然后将其水平投影（圆）和正面投影上的导程分 成相同的等分（图中为12等分）。 (2)从导程上各分点作水平线，再从圆周上各分点作垂直投影连线，它们相应的交点 如a9、a9、a9.,即为螺旋线上各点的正面投影。 (3)依次光滑地连接这些点的投影即得螺旋线的正面投影，在可见圆柱面上的螺旋线是 可见的，其投影画成实线，在不可见圆柱面上的螺旋线是不可见的，其投影画成虚线，螺旋 线的水平投影重影在圆柱面的水平投影圆周上。 如将圆柱表面展开，则螺旋线随之展成一直线（图5-9），该直线为直角三角形的斜边， 底边为圆柱面圆周的周长（πd),高为螺旋线的导程(P)。显然螺旋线的一个导程的长度 为Vd}+P ，直角三角形斜边与底边的夹角α称为螺旋线的升角。 a-arctan P. 斜边与另一直角边的夹角称为螺旋角，以B表示，由此可见a+B=90°。 22

123 ( ) 2 2 d + Pn 用换面法来作出其长短轴（图 5-8）。如作圆的水平投影，首先将四边形平面变换成投影面垂 直面，即以 V1 面代替 V 面，则在 V1/H 体系中圆为垂直面，可根据圆在投影面垂直面上的作 图方法作出其投影。圆的正面投影也可类似地作出。 5.1.2 圆柱螺旋线 圆柱螺旋线是工程上应用最广泛的空间曲线。下面讨论其形成及投影作图方法。 1.圆柱螺旋线的形成 一动点在正圆柱表面上绕其轴线作等速回转运动，同时沿圆柱的 轴线方向作等速直线运动，则动点在圆柱表面上的轨迹称为圆柱螺旋线。如图 5-9a 所示，点 A 的轨迹即为圆柱螺旋线。点 A 旋转一圈沿轴向移动的距离（如 A0A12）称为导程（Pn）。当 圆柱的轴线为铅垂线时，从前方垂直向后看，如螺旋线的可见部分为自左向右上升的则称为 右旋螺旋线，反之称为左旋螺旋线。 2.圆柱螺旋线的投影作图方法 圆柱直径为 d，导程为 Pn 的右旋螺旋线，其投影的作图 步骤如下（图 5-9b）： （1）作出直径为 d 的圆柱面的两投影，然后将其水平投影（圆）和正面投影上的导程分 成相同的等分（图中为 12 等分）。 （2）从导程上各分点作水平线，再从圆周上各分点作垂直投影连线，它们相应的交点， 如 a0、a1、a2.，即为螺旋线上各点的正面投影。 （3）依次光滑地连接这些点的投影即得螺旋线的正面投影，在可见圆柱面上的螺旋线是 可见的，其投影画成实线，在不可见圆柱面上的螺旋线是不可见的，其投影画成虚线，螺旋 线的水平投影重影在圆柱面的水平投影圆周上。 如将圆柱表面展开，则螺旋线随之展成一直线（图 5-9c），该直线为直角三角形的斜边， 底边为圆柱面圆周的周长（πd），高为螺旋线的导程（Pn）。显然螺旋线的一个导程的长度 为 ，直角三角形斜边与底边的夹角α称为螺旋线的升角。 斜边与另一直角边的夹角称为螺旋角，以β表示，由此可见 α+β＝90°。 A A A A A A A A A A A A A A a a a a a a a a a a a a a d a） b） c） 图 5-9 圆柱螺旋线的形成、投影和展开 d Pn π  = arc t an

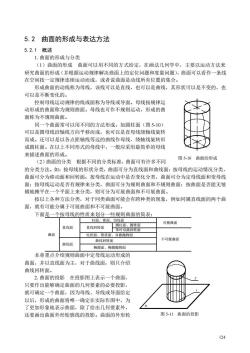
5.2曲面的形成与表达方法 5.2.1概述 1.曲面的形成与分类 (1)曲面的形成曲面可以用不同的方式给定，在画法几何学中，主要以运动方法来 研究曲面的形成（并根据运动规律解决曲面上的定位问题和度量问题），曲面可以看作一条线 在空间按一定规律连续运动而成，或者说曲面是动线所有位置的集合。 形成曲面的动线称为母线，该线可以是直线，也可以是曲线，其形状可以是不变的，也 可以是不断变化的。 控制母线运动规律的线或面称为导线或导面。母线按规律运 动形成的曲面称为规则曲面。母线也可作不规则运动，形成的曲 面称为不规则曲面。 同一个曲面常可以用不同的方法形成。如圆柱面（图5-10） 可以是圆母线沿轴线方向平移而成，也可以是直母线绕轴线旋转 而成。还可以是以各点距轴线等远的曲线作母线，绕轴线旋转形 成圆柱面。在以上不同形式的母线中，一般应采用最简单的母线 来描述曲面的形成。 (2)曲面的分类根据不同的分类标准，曲面可有许多不同 图5-10曲面的形成 的分类方法。如：按母线的形状分类，曲面可分为直线面和曲线面：按母线的运动情况分类 曲面可分为移动面和回转面：按母线在运动中是否变化分类，曲面可分为定母线面和变母线 面：按母线运动是否有规律来分类，曲面可分为规则曲面和不规则曲面：按曲面是否能无皱 褚地难平在一个平面上来分类，则可分为可展曲面和不可展曲面。 按以上各种方法分类，对于同类曲面可能会有跨种类的现象，例如同属直线面的两个曲 面，就有可能分属于可展曲面和不可展曲面。 下面是一个按母线的性质来划分一些规则曲面的简表： 可展幽面 直线面 直线回转面 双曲回转 双曲物面 不可展曲面 曲线面 椭圆面、韩阅抛物面 本章重点介绍规则曲面中定母线运动形成的 曲面，并以直线面为主，对于曲线面，则只介死 曲线回转面。 2.曲面的投影在投影图上表示一个曲面， 只要作出能够确定曲面的几何要素的必要投影， 就可确定一个曲面，因为母线、导线或导面给定 以后，形成的曲面将唯一确定在实际作图中，为 了更加形象地表示曲面，除了给出几何要素外， 还要画出曲面外形轮廓线的投影。曲面的外形轮 图5-11曲面的投影 124

124 5.2 曲面的形成与表达方法 5.2.1 概述 1.曲面的形成与分类 （1）曲面的形成 曲面可以用不同的方式给定，在画法几何学中，主要以运动方法来 研究曲面的形成（并根据运动规律解决曲面上的定位问题和度量问题），曲面可以看作一条线 在空间按一定规律连续运动而成，或者说曲面是动线所有位置的集合。 形成曲面的动线称为母线，该线可以是直线，也可以是曲线，其形状可以是不变的，也 可以是不断变化的。 控制母线运动规律的线或面称为导线或导面。母线按规律运 动形成的曲面称为规则曲面。母线也可作不规则运动，形成的曲 面称为不规则曲面。 同一个曲面常可以用不同的方法形成。如圆柱面（图 5-10） 可以是圆母线沿轴线方向平移而成，也可以是直母线绕轴线旋转 而成。还可以是以各点距轴线等远的曲线作母线，绕轴线旋转形 成圆柱面。在以上不同形式的母线中，一般应采用最简单的母线 来描述曲面的形成。 （2）曲面的分类 根据不同的分类标准，曲面可有许多不同 的分类方法。如：按母线的形状分类，曲面可分为直线面和曲线面；按母线的运动情况分类， 曲面可分为移动面和回转面；按母线在运动中是否变化分类，曲面可分为定母线面和变母线 面；按母线运动是否有规律来分类，曲面可分为规则曲面和不规则曲面；按曲面是否能无皱 褶地摊平在一个平面上来分类，则可分为可展曲面和不可展曲面。 按以上各种方法分类，对于同类曲面可能会有跨种类的现象，例如同属直线面的两个曲 面，就有可能分属于可展曲面和不可展曲面。 下面是一个按母线的性质来划分一些规则曲面的简表： 曲面 直线面 柱面、锥面、切线面 可展曲面 直线回转面 圆柱面、圆锥面 单叶双曲回转面 不可展曲面 柱状面、锥状面、双曲抛物面 曲线面 曲线回转面 椭圆面、椭圆抛物面 本章重点介绍规则曲面中定母线运动形成的 曲面，并以直线面为主，对于曲线面，则只介绍 曲线回转面。 2.曲面的投影 在投影图上表示一个曲面， 只要作出能够确定曲面的几何要素的必要投影， 就可确定一个曲面，因为母线、导线或导面给定 以后，形成的曲面将唯一确定在实际作图中，为 了更加形象地表示曲面，除了给出几何要素外， 还要画出曲面外形轮廓线的投影。曲面的外形轮 图 5-10 曲面的形成 T t H 图 5-11 曲面的投影

廓线就是在正投影条件下，包络己知曲面的投射柱面与曲面的切线。 曲面的外形轮廓线对不同投影面各不相同。如图5-11所示，投射柱面与曲面的切线T称 为曲面对H面的轮廓线，而1则称为曲面轮廓线的H投影。 当曲面轮廓线与曲面的某些位置的母线重合时，这些母线称为转向轮常线。 5.2.2柱面 1.柱面的形成一直母线沿着一曲导线运动且始终平行于直导线而形成的曲面称为柱 面。曲导线可以是闭合的，也可以是不闭合的。如图512所示，【为母线，Q为曲导线 AB为直导线，当母线/∥沿着曲导线Q运动，且平行于直导线AB,所形成的曲面即为柱面。 由于柱面上连续两素线是平行两直线，能组成一平面，因此柱面是一种可展直线面 0导 b) 图512柱面的形成和投影 2.柱面的投影在投影图上表达柱面一般要画出导线及曲面的外形轮廓线，必要时还要 画出若干素线。如图5-12b,导线Q为平行于H面的圆，导线AB为一般位置直线，表示这 一柱面时，可先画出Q的正面投影和水平投影，Q即为柱面的顶圆，其底圆平行于顶圆Q, 顶圆和底圆的圆心连线O0即为该柱面的轴线，轴线必定平行于直导线AB,由于素线的方向 可由轴线控制，因此直导线AB可以不再画出。最后画出柱面的外形轮廓线，如在正面投影 上，顶圆和底圆最左、最右点投影的连线，即为前后曲面转向线的投影，在水平投影上为两 圆的公切线，它们是上、下曲面转向线的投影。这些外形轮廓线均应平行于轴线的同面投影。 5.23维面 1,锥面的形成 一直母线沿一曲导线运动且始终通过一定点而形成的曲面称为锥面。该 定点称为导点，即为锥面顶点。如图5-13a所示，SI为母线，Q为曲导线，S为导点，当母 线S/沿着曲导线Q运动，且始终通过导点S,所形成的曲面即为锥面。由于锥面上相邻两 素线必定为过锥顶的相交两直线，因此锥面也是一种可展直线面。 2.锥面的投影在投影图上表达锥面一般只要画出导点（锥项）、导线以及曲面的外形 轮廓线，必要时还要画出若干素线。如图5-13b所示，导线Q为一水平圆，导点S和导圆的 中心O的连线为一正平线，分别作出S点和Q圆的两个投影，然后作出其外形轮廊线，也就 是锥面转向轮廓线的投影。 由于锥面的轴线是锥面两对称平面的交线，在图示情况下，SO连线并不是锥面的轴线， 而其轴线为SO,其投影s01、s909分别平分水平投影和正面投影两外形轮廓线所形成的夹角

125 廓线就是在正投影条件下，包络已知曲面的投射柱面与曲面的切线。 曲面的外形轮廓线对不同投影面各不相同。如图 5-11 所示，投射柱面与曲面的切线 T 称 为曲面对 H 面的轮廓线，而 t 则称为曲面轮廓线的 H 投影。 当曲面轮廓线与曲面的某些位置的母线重合时，这些母线称为转向轮廓线。 5.2.2 柱面 1．柱面的形成 一直母线沿着一曲导线运动且始终平行于直导线而形成的曲面称为柱 面。曲导线可以是闭合的，也可以是不闭合的。如图 5-12a 所示，ⅠⅡ为母线，Q 为曲导线， AB 为直导线，当母线ⅠⅡ沿着曲导线 Q 运动，且平行于直导线 AB，所形成的曲面即为柱面。 由于柱面上连续两素线是平行两直线，能组成一平面，因此柱面是一种可展直线面。 2．柱面的投影 在投影图上表达柱面一般要画出导线及曲面的外形轮廓线，必要时还要 画出若干素线。如图 5-12b，导线 Q 为平行于 H 面的圆，导线 AB 为一般位置直线，表示这 一柱面时，可先画出 Q 的正面投影和水平投影，Q 即为柱面的顶圆，其底圆平行于顶圆 Q， 顶圆和底圆的圆心连线 OO 即为该柱面的轴线，轴线必定平行于直导线 AB，由于素线的方向 可由轴线控制，因此直导线 AB 可以不再画出。最后画出柱面的外形轮廓线，如在正面投影 上，顶圆和底圆最左、最右点投影的连线，即为前后曲面转向线的投影，在水平投影上为两 圆的公切线，它们是上、下曲面转向线的投影。这些外形轮廓线均应平行于轴线的同面投影。 5.2.3 锥面 1．锥面的形成 一直母线沿一曲导线运动且始终通过一定点而形成的曲面称为锥面。该 定点称为导点，即为锥面顶点。如图 5-13a 所示，SⅠ为母线，Q 为曲导线，S 为导点，当母 线 SⅠ沿着曲导线 Q 运动，且始终通过导点 S，所形成的曲面即为锥面。由于锥面上相邻两 素线必定为过锥顶的相交两直线，因此锥面也是一种可展直线面。 2．锥面的投影 在投影图上表达锥面一般只要画出导点（锥顶）、导线以及曲面的外形 轮廓线，必要时还要画出若干素线。如图 5-13b 所示，导线 Q 为一水平圆，导点 S 和导圆的 中心 O 的连线为一正平线，分别作出 S 点和 Q 圆的两个投影，然后作出其外形轮廓线，也就 是锥面转向轮廓线的投影。 由于锥面的轴线是锥面两对称平面的交线，在图示情况下，SO 连线并不是锥面的轴线， 而其轴线为 SO1，其投影 so1、so1分别平分水平投影和正面投影两外形轮廓线所形成的夹角。 A B O O a b X o o q 1 2 Q导线 导线 母线 a b 2 o 1 o q a） b） 图 5-12 柱面的形成和投影

a) b) 图513锥面的形成和投影 5.2.4曲线回转面 1.曲线回转面的形成任意一曲线绕 一轴线（即导线）回转而形成的曲面称为 曲线回转面。如图5-14a所示，平面曲线 ABCD为母线，OO为轴线，回转时曲线 两端点A、D形成的圆为曲面的顶圆和底 最小网（喉 母 圆，曲线上距离轴线最近的点B和最远的 最大圆（赤道圆 点C形成的圆分别为最小圆（喉圆）和最 大圆（赤道圆）。 底圆 2.曲线回转面的投影在投影图上表 示曲线回转面通常要画出其轴线、顶圆、 底圆、最小圆和最大圆等的投影及其外形 图5-14曲线回转面的形成和投是 轮廓线。如图5-14b示，一般在反映轴线 的投影图上不必画出最小圆和最大圆的投影。 5.2.5螺旋面 1.正螺旋面 (1)正螺旋面的形成 一直母线沿着曲导线为圆柱螺旋线及直导线为圆柱轴线运动，且 始终与轴线垂直相交，该母线运动的轨迹即为圆柱正螺旋面。如图5-15所示，圆柱轴线垂 直H面，直母线平行H面且与轴线相交。正螺旋面是一种不可展的直线面。 (2)正螺旋面的投影投影图上一般要画出曲导线（螺旋线）、直导线（轴线）以及若 干直素线。如图5-15所示。作图时先画出轴线O0及螺旋线的投影，如螺旋线的导程为P。, 母线的长为L,将导程P。内的轴线和螺旋线分成相同的若干等分，对应点的连线即为正螺旋 面的若干素线OA、IA1、4.(其长度均等于L)的投影。导程为P的圆柱螺旋线的投 影也是正螺旋面的外形轮廓线。 如另一同轴线的圆柱面与正螺旋面相交，其交线BBB:.为另一圆柱螺旋线，它与原来 的螺旋线具有相同的导程，但圆柱面直径较小，故导程角较大，如图5-15b所示。图5-15d 126

126 5.2.4 曲线回转面 1．曲线回转面的形成 任意一曲线绕 一轴线（即导线）回转而形成的曲面称为 曲线回转面。如图 5-14a 所示，平面曲线 ABCD 为母线，OO 为轴线，回转时曲线 两端点 A、D 形成的圆为曲面的顶圆和底 圆，曲线上距离轴线最近的点 B 和最远的 点 C 形成的圆分别为最小圆（喉圆）和最 大圆（赤道圆）。 2．曲线回转面的投影 在投影图上表 示曲线回转面通常要画出其轴线、顶圆、 底圆、最小圆和最大圆等的投影及其外形 轮廓线。如图 5-14b 示，一般在反映轴线 的投影图上不必画出最小圆和最大圆的投影。 5.2.5 螺旋面 1.正螺旋面 （1）正螺旋面的形成 一直母线沿着曲导线为圆柱螺旋线及直导线为圆柱轴线运动，且 始终与轴线垂直相交，该母线运动的轨迹即为圆柱正螺旋面。如图 5-15a 所示，圆柱轴线垂 直 H 面，直母线平行 H 面且与轴线相交。正螺旋面是一种不可展的直线面。 （2）正螺旋面的投影 投影图上一般要画出曲导线（螺旋线）、直导线（轴线）以及若 干直素线。如图 5-15c 所示。作图时先画出轴线 OO 及螺旋线的投影，如螺旋线的导程为 Pn， 母线的长为 L，将导程 Pn 内的轴线和螺旋线分成相同的若干等分，对应点的连线即为正螺旋 面的若干素线 OA0、ⅠA1、ⅡA2.（其长度均等于 L）的投影。导程为 Pn 的圆柱螺旋线的投 影也是正螺旋面的外形轮廓线。 如另一同轴线的圆柱面与正螺旋面相交，其交线 B0B1B2.为另一圆柱螺旋线，它与原来 的螺旋线具有相同的导程，但圆柱面直径较小，故导程角较大，如图 5-15b 所示。图 5-15d S O X o s o 1 母线 导线 Ⅰ 1 o o s a） b） 图 5-13 锥面的形成和投影 A O B C D O a o b d o c d a b o c 顶圆 母线 最小圆（喉圆 最大圆（赤道圆 底圆 a） b） 图 5-14 曲线回转面的形成和投影

为其投影图。 0 图5-15正螺旋面的形成和投影 2.斜螺旋面 (1)斜螺旋面的形成一直母线沿者曲导线为圆柱螺旋线及直导线为圆柱轴线运动，且 始终与轴线成相同角度倾斜（也即与轴线所垂直的平面成相同倾角）而形成的曲面称为斜螺 旋面。如图5-16所示，直素线OA、IA、4，.与H面的倾角均为a角。如以OA,为直母 线绕轴线旋转形成一圆锥面，由于圆锥面上的每一条素线均与H面成a角，因此斜螺旋面的 素线必与圆锥面上某一相应素线平行，所以上述圆锥面又称为斜螺旋面的导锥面。斜螺旋面 也是一种不可展的直线面。 (2)斜螺旋面的投影在投影图上一般要画出曲导线（圆柱螺旋线）、直导线（圆柱轴 线)以及若干直素线，同时要画出其外形轮廓线，在正面投影上即为直素线投影的包络线

127 为其投影图。 2.斜螺旋面 （1）斜螺旋面的形成 一直母线沿着曲导线为圆柱螺旋线及直导线为圆柱轴线运动，且 始终与轴线成相同角度倾斜（也即与轴线所垂直的平面成相同倾角）而形成的曲面称为斜螺 旋面。如图 5-16 所示，直素线 OA0、ⅠA1、ⅡA2.与 H 面的倾角均为α角。如以 OA0 为直母 线绕轴线旋转形成一圆锥面，由于圆锥面上的每一条素线均与 H 面成α角，因此斜螺旋面的 素线必与圆锥面上某一相应素线平行，所以上述圆锥面又称为斜螺旋面的导锥面。斜螺旋面 也是一种不可展的直线面。 （2）斜螺旋面的投影 在投影图上一般要画出曲导线（圆柱螺旋线）、直导线（圆柱轴 线）以及若干直素线，同时要画出其外形轮廓线，在正面投影上即为直素线投影的包络线。 P 2 A6 a6 A0 a0 a1 A1 a2 A2 2 A0 a0 a6 A6 B B B a a a a b b o b a a a a a b b b o b a a a a a a a a a a a 6 2 1 o a L 12 o a a b b a b o b o b O n Pn Pn c) d) 图 5-15 正螺旋面的形成和投影 a） b）

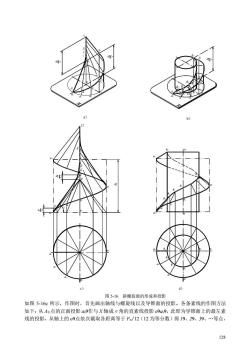
c) 图5-16斜螺旋面的形成和投影 如图5-16c所示，作图时，首先画出轴线与螺旋线以及导锥面的投影。各条素线的作图方法 如下：从Ao点的正面投影a9作与X轴成a角的直素线投影o9a9,此即为导锥面上的最左素 线的投影，从轴上的9点依次截取各距离等于P/12(12为等分数)得19、29、39、.等点 128

128 2 o A A A A A a a a a o a a a a a b b b b b B B B B a a a a a a a a a o a 0 1 2 3 6 a 12 12 b o a b a a a a a b b b b o a a a a b a b b b b 2 a 2 A A A A A o 12 Pn p Pn Pn nP nP c） d） 图 5-16 斜螺旋面的形成和投影 如图 5-16c 所示，作图时，首先画出轴线与螺旋线以及导锥面的投影。各条素线的作图方法 如下：从 A0 点的正面投影 a0作与 X 轴成α角的直素线投影 oa0，此即为导锥面上的最左素 线的投影，从轴上的 o点依次截取各距离等于 Pn/12（12 为等分数）得 1、2、3、.等点， a） b）

与螺旋线投影上的a19、a9、a9.等点连接，即得素线IA、ⅡA、4.等的正面投影， 其19a9、29a29、39a9.等必与导锥面上相应素线的正面投影相平行。作这些素线投影的包 络线即为斜螺旋面的外形轮廓线。 图5-16b、d为此斜螺旋面与同轴的圆柱面相交于另一螺旋线BoBB2.,它与原来螺旋线 具有相同的导程，但直径较小，因而导程角较大。 观察与思考：观察周围哪些物体为曲面，这些曲面都由什么形状的母线和导线形成，如 车、船、飞机外壳，杯子、牙刷、笔等，并试着图示之。 复习思考题 一、基本问题 1.试述平行、垂直和倾斜于投影面的圆的投影特性。 2.位于一般位置平面上的圆的投影作图有几种方法？ 3.什么是圆柱螺旋线的基本要素？ 4.什么是曲面的母线？什么是曲面的素线？什么是曲面对投影面的转向轮廓线？ 5.试作一曲面分类一览表。 6.画曲线、曲面投影图的最基本的方法是什么？ 二、是非问题 1.曲线的投影相对于该曲线同阶或低一阶。 2.用投影表示曲面时，只需要画出曲面外形轮廓线的投影，不需要画出母线和导线或导面的投 影。 三、综合问题 L.表示空间曲线K在点M处的切线和法平面。（题目5-1） 2.可有办法解决直线4B与斜锥面的交点问题。（题目5-2） 题目5-】 题目5-2 129

129 与螺旋线投影上的 a1、a2、a3.等点连接，即得素线ⅠA1、ⅡA2、ⅢA3.等的正面投影， 其 1a1、2a2、3a3.等必与导锥面上相应素线的正面投影相平行。作这些素线投影的包 络线即为斜螺旋面的外形轮廓线。 图 5-16b、d 为此斜螺旋面与同轴的圆柱面相交于另一螺旋线 B0B1B2.，它与原来螺旋线 具有相同的导程，但直径较小，因而导程角较大。 观察与思考：观察周围哪些物体为曲面，这些曲面都由什么形状的母线和导线形成，如 车、船、飞机外壳，杯子、牙刷、笔等，并试着图示之。 复习思考题 一、基本问题 1．试述平行、垂直和倾斜于投影面的圆的投影特性。 2．位于一般位置平面上的圆的投影作图有几种方法？ 3．什么是圆柱螺旋线的基本要素？ 4．什么是曲面的母线？什么是曲面的素线？什么是曲面对投影面的转向轮廓线？ 5．试作一曲面分类一览表。 6．画曲线、曲面投影图的最基本的方法是什么？ 二、是非问题 1. 曲线的投影相对于该曲线同阶或低一阶。.（ ） 2. 用投影表示曲面时，只需要画出曲面外形轮廓线的投影，不需要画出母线和导线或导面的投 影。.（ ） 三、综合问题 1. 表示空间曲线 K 在点 M 处的切线和法平面。（题目 5-1） 2. 可有办法解决直线 AB 与斜锥面的交点问题。（题目 5-2） k′ ′ ′ ′ ′ a b b a o1 o1 s s k m m′ X X O O 题目 5-1 题目 5-2