《画法几何与工程制图》课程教学资源（教材讲义）第04章 立体及其表面交线

第6章立体及其表面交线 本章内容是在研究点、线、面投影的基础上进一步论述立体的投影作图问题 6.1立体的投影 立体是由其表面所围成的。表面均为平面的立体称为平面立体，表面为曲面或平面与 曲面的立体称为曲面立体。在投影图上表示一个立体，就是把这些平面和曲面表达出来， 然后根据可见性原理判别线条的可见性，把其投影分别画成实线或虚线，即得立体的投影 图。 6.1.1.平面立体的投影 平面立体主要有棱柱、棱锥等。在投影图上表示平面立体就是把围成立体的平面及其 棱线表示出米，然后判别其可见性，把看得见的棱线投影画成实线，看不见的棱线的投影 画成虑线。 1.棱柱 (1)棱柱的投影图6-1为一正六棱柱，其顶面、底面均为水平面，它们的水平投影 反映实形，正面及侧面投影积聚为直线。棱柱有六个侧棱面，前后棱面为正平面，它们的 正面投影反映实形：水平及侧面投影积聚为一直线：棱柱的其它四个侧棱面均为铅垂面， 其水平投影均积聚为直线，正面和侧面投影均为类似形。 图61正六棱柱的投影及表面上取点 棱线AB为铅垂线，其水平投影积聚为一点ā(b),正面和侧面投影均反映实长，即 ab=ab守=AB。顶面的边DE为侧垂线，侧面投影积聚为一点d号(e),水平投影 和正面投影均反缺实长，即de=d件=DE。底面的边BC为水平线，水平投影反映实长， 即b=BC,正面投影bc4和侧面投影b背c均小于实长。其余棱线，可自行分析。 作图时可先画正六棱柱的水平投影正六边形，再根据投影规律作出其它两个投影。 (2)棱柱表面上取点在平面立体表面上取点，其原理和方法与在平面上取点相同。 30

130 第 6 章 立体及其表面交线 本章内容是在研究点、线、面投影的基础上进一步论述立体的投影作图问题。 6.1 立体的投影 立体是由其表面所围成的。表面均为平面的立体称为平面立体，表面为曲面或平面与 曲面的立体称为曲面立体。在投影图上表示一个立体，就是把这些平面和曲面表达出来， 然后根据可见性原理判别线条的可见性，把其投影分别画成实线或虚线，即得立体的投影 图。 6.1.1. 平面立体的投影 平面立体主要有棱柱、棱锥等。在投影图上表示平面立体就是把围成立体的平面及其 棱线表示出来，然后判别其可见性，把看得见的棱线投影画成实线，看不见的棱线的投影 画成虚线。 1.棱柱 （1）棱柱的投影 图 6-1 为一正六棱柱，其顶面、底面均为水平面，它们的水平投影 反映实形，正面及侧面投影积聚为直线。棱柱有六个侧棱面，前后棱面为正平面，它们的 正面投影反映实形；水平及侧面投影积聚为一直线；棱柱的其它四个侧棱面均为铅垂面， 其水平投影均积聚为直线，正面和侧面投影均为类似形。 棱线 AB 为铅垂线，其水平投影积聚为一点 a（b），正面和侧面投影均反映实长，即 ab＝ab＝AB。顶面的边 DE 为侧垂线，侧面投影积聚为一点 d （e），水平投影 和正面投影均反映实长，即 de＝de＝DE。底面的边 BC 为水平线，水平投影反映实长， 即 bc＝BC，正面投影 bc和侧面投影 bc均小于实长。其余棱线，可自行分析。 作图时可先画正六棱柱的水平投影正六边形，再根据投影规律作出其它两个投影。 （2）棱柱表面上取点 在平面立体表面上取点，其原理和方法与在平面上取点相同。 d c m b c e n a d b c m a d n e n e m b a 图 6-1 正六棱柱的投影及表面上取点 a d e b c d  a a (b) d (e ) b c (c) e H A B E C D V W

由于图6-1中所示正六棱柱的各个表面都处于特殊位置，因此在表面上取点可利用积聚性 原理作图。 如已知棱柱表面上点M的正面投影m1,要求出其它两投影m、m守。由于点M是可见 的，因此，点M必定在ABCD棱面上，而ABCD棱面为铅垂面，水平投影a(bcd有积聚 性，因此m必在a(bcd上，根据m和m即可求出m。又如已知点N的水平投影n, 要求出其它两投影nt、。由于点N是可见的，因此点N必定在顶面上，而顶面的正 面投影和侧面投影都具有积聚性，因此n、必定在顶面的同面投影上。 2.棱锥 (1)棱锥的投影如图6-2所示为一正三棱锥，锥顶为S,其底面为△4BC,呈水平 位置，其水平投影△abc反映实形。棱面△SAB、△SBC是一般位置平面，它们的各个投影 均为类似形。棱面△SAC为侧垂面，其侧面投影△sac“积聚为一直线。底边AB、BC 为水平线，CA为侧垂线，棱线SB为侧平线，SA、SC为倾斜线，它们的投影可根据不同 位置直线的投影特性进行分析 作图时先画出底面△ABC的各个投影，再作出锥顶S的各个投影，然后连接各棱线即 图62正三棱锥的投影及表面取点图 得正三棱锥的三面投影 (2)棱锥表面上取点如已知点M的正面投影mA,要求出点M的其它投影m,m: 由于点M在棱面△S4B上，因此过点M在△SAB上作AB的平行线IM,即作1mA∥abM, 再作lm∥ab,求出m,再根据m、mt求出m。也可过锥顶S和点M作一辅助线S 然后求出点M的水平投影m,再由m、mA求出点M的侧面投影m逍。又如已知点N的水 平投影n,要求出点N的其它投影n、n。由于点N在侧垂面△SAC上，因此n必定在 △s尚ac当上，由n、n进可求出(n4)。 6.1.2曲面立体的投影 工程中常见的曲面立体是回转体，主要有圆柱、圆锥、球、环等，在投影图上表示回 转体就是把组成立体的回转面或平面和回转面表示出来，然后判别其可见性。 1.圆柱圆柱表面由圆柱面和项、底圆所组成。圆柱面是一直母线绕与之平行的轴线 回转而成，如图6-3a所示。 (1)圆柱的投影如图6-3b所示，圆柱的轴线垂直于H面，其上、下底圆为水平面， 水平投影反映实形，其正面和侧面投影积聚为一直线。圆柱面的水平投影也积聚为一圆 13

131 由于图 6-1 中所示正六棱柱的各个表面都处于特殊位置，因此在表面上取点可利用积聚性 原理作图。 如已知棱柱表面上点 M 的正面投影 m，要求出其它两投影 m、m。由于点Ｍ是可见 的，因此，点 M 必定在 ABCD 棱面上，而 ABCD 棱面为铅垂面，水平投影 a(b)(c)d 有积聚 性，因此 m 必在 a(b)(c)d 上，根据 m和 m 即可求出 m。又如已知点 N 的水平投影 n， 要求出其它两投影 n、 n。由于点 N 是可见的，因此点 N 必定在顶面上，而顶面的正 面投影和侧面投影都具有积聚性，因此 n、n必定在顶面的同面投影上。 2.棱锥 （1）棱锥的投影 如图 6-2 所示为一正三棱锥，锥顶为 S，其底面为△ABC，呈水平 位置，其水平投影△abc 反映实形。棱面△SAB、△SBC 是一般位置平面，它们的各个投影 均为类似形。棱面△SAC 为侧垂面，其侧面投影△sac"积聚为一直线。底边 AB、BC 为水平线，CA 为侧垂线，棱线 SB 为侧平线，SA、SC 为倾斜线，它们的投影可根据不同 位置直线的投影特性进行分析。 作图时先画出底面△ABC 的各个投影，再作出锥顶 S 的各个投影，然后连接各棱线即 得正三棱锥的三面投影。 （2）棱锥表面上取点 如已知点Ｍ的正面投影 m，要求出点 M 的其它投影 m、m。 由于点 M 在棱面△SAB 上，因此过点Ｍ在△SAB 上作 AB 的平行线ⅠM，即作 1m∥ab， 再作 1m∥ab，求出 m，再根据 m、m求出 m。也可过锥顶 S 和点 M 作一辅助线 SⅡ， 然后求出点 M 的水平投影 m，再由 m、m求出点 M 的侧面投影 m。又如已知点 N 的水 平投影 n，要求出点 N 的其它投影 n、n。由于点 N 在侧垂面△SAC 上，因此 n必定在 △sac上，由 n、n可求出（n）。 6.1.2 曲面立体的投影 工程中常见的曲面立体是回转体，主要有圆柱、圆锥、球、环等，在投影图上表示回 转体就是把组成立体的回转面或平面和回转面表示出来，然后判别其可见性。 1.圆柱 圆柱表面由圆柱面和顶、底圆所组成。圆柱面是一直母线绕与之平行的轴线 回转而成，如图 6-3a 所示。 （1）圆柱的投影 如图 6-3b 所示，圆柱的轴线垂直于 H 面，其上、下底圆为水平面， 水平投影反映实形，其正面和侧面投影积聚为一直线。圆柱面的水平投影也积聚为一圆， c a b m n s s n m b c a 2 1 n s m 2 c b a 图 6-2 正三棱锥的投影及表面取点图 a s b s a a c s b (c ) b H A B C S V W

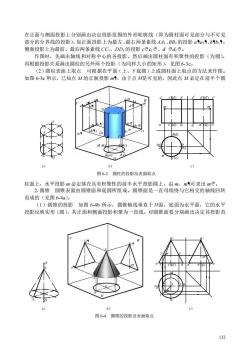
在正面与侧面投影上分别画出决定投影范围的外形轮廓线（即为圆柱面可见部分与不可见 部分的分界线的投景影)，如正面投影上为最左、最右两条素线AA1、BB,的投影aa,、bb,年： 训面投母影上为最前、最后两条素线CC,、DD,的投号影c物C、d特d,博。 作图时，先画出轴线和对称中心的各投影，然后画出圆柱面有积聚性的投影（为圆）， 再根据投影关系画出圆柱的另外两个投影（为同样大小的矩形），见图6-3c。 (2)圆柱表面上取点可根据在平面（上、下底圆）上或圆柱面上取点的方法来作图 如图6-3C所示，己知点M的正面投影m1,由于点M是可见的，因此点M必定在前半个圆 b) 图63圆柱的投影及表面取点 柱面上，水平投影m必定落在具有积聚性的前半水平投影圆上，由m、m可求出m增。 2.圆锥圆锥表面由圆锥面和底圆所组成。圆锥面是一直母线绕与它相交的轴线回转 而成的（见图64a)。 (1)圆锥的投影如图6-4b所示，圆锥轴线垂直于H面，底面为水平面，它的水平 投影反映实形（圆），其正面和侧面投影积聚为一直线。对圆锥面要分别画出决定其投影范 b) 图64圆锥的投影及表面取点 132

132 在正面与侧面投影上分别画出决定投影范围的外形轮廓线（即为圆柱面可见部分与不可见 部分的分界线的投影），如正面投影上为最左、最右两条素线 AA1、BB1 的投影 aa1、bb1； 侧面投影上为最前、最后两条素线 CC1、DD1 的投影 cc1、d d1。 作图时，先画出轴线和对称中心的各投影，然后画出圆柱面有积聚性的投影（为圆）， 再根据投影关系画出圆柱的另外两个投影（为同样大小的矩形），见图 6-3c。 （2）圆柱表面上取点 可根据在平面（上、下底圆）上或圆柱面上取点的方法来作图。 如图 6-3c 所示，已知点 M 的正面投影 m，由于点Ｍ是可见的，因此点 M 必定在前半个圆 柱面上，水平投影 m 必定落在具有积聚性的前半水平投影圆上，由 m、m可求出 m。 2.圆锥 圆锥表面由圆锥面和底圆所组成。圆锥面是一直母线绕与它相交的轴线回转 而成的（见图 6-4a）。 （1）圆锥的投影 如图 6-4b 所示，圆锥轴线垂直于Ｈ面，底面为水平面，它的水平 投影反映实形（圆），其正面和侧面投影积聚为一直线。对圆锥面要分别画出决定其投影范 O O A A 1 1 a b c d m a c d b m d a b c m ( ) ( ) a c (d ) b d a (b ) 1 1 1 1 c 1 1 1 1 (a1) (d1) (b1) (c1) a） b） c） 图 6-3 圆柱的投影及表面取点 O S A O a b c d s m 2 3 1 s 3 c d b 2 m a 1 s m c ( ) d a (b) 1 a） b） c） 图 6-4 圆锥的投影及表面取点 a (d ) b c d  a(a1) a d( d1) (b1) (b ) c c(c1 ) H A B C D V W (d1) b1 c1 a1 d1 a1  (b1 ) c1  b A1 B1 C1 D1 a s s a a s H A S V W

围的外形轮廓线，如正面投影上为最左、最右两条素线S4、SB的投影sa4、s4bM,侧面 投影上为最前、最后两条素线SC、SD的投影sc、sd曹。 作图时，先画出轴线和对称中心的各投影：然后画出底面的各个投影及锥顶点的投影， 再分别画出其外形轮廓线，即完成圆锥的各个投影（见图64c)。 (2)圆锥表面上取点 可根据圆锥面的形成特性来作图。如图6-4c所示，己知圆细 面上点M的正面投影mA,可采用下列两种方法求出点M的水平投影m和侧面投影m净。 方法一：辅助素线法过锥顶S和点M作一辅助线SI,根据已知条件可以确定S的 正面投影s411,然后求出它的水平投影s1、侧面投影s1边，再由m4根据点在直线上的 投影性质求出m和m。 方法二：辅助圆法过点M作一平行于底面的水平辅助圆，该圆的正面投影为过m 且平行于4b4的直线2431，它的水平投影为一直径等于231的圆，m必在此圆周上，由 m求出m,再由m、m求出m。 3.球球的表面是球面。球面是一个圆母线绕其过圆心且在同一平面上的轴线回转而 形成的（图6-5a)。 (1)球的投影如图65b所示，球的三个投影均为圆，其直径与球直径相等，但三 个投影面上的圆是不同的转向线的投影，正面投影上的圆是平行于V面的最大圆的投影 b) c) 图65球的投形及表面取点 (区分前、后半球表面的外形轮廓线)，水平投影上的圆是平行于H面的最大圆的投影（区 分上、下半球表面的外形轮廓线)，侧面投影上的圆是平行于W面的最大圆的投影（区别 左、右半球表面的外形轮廓线)。 作图时，可先画出确定球心的三个投影，再以球心为圆心画出三个与圆球直径相等的 圆。 (2)球面上取点如图6-5c所示，己知球面上点M的水平投影m,要求出其m4和 m遗。可过点M作一平行于V面的辅助圆，它的水平投影为12，正面投影为直径等于121 的圆，m必定在该圆上，由m可求得m，由m和m可求出m3。显然，点M在前半球 面上，因此从前向后看是可见的，同理，点M在左半球面上，从左向右看也是可见的。 当然，也可作平行于H面的辅助圆来作图，读者自行分析并想像当点位于后半球时， 133

133 围的外形轮廓线，如正面投影上为最左、最右两条素线 SA、SＢ的投影 sa、sb，侧面 投影上为最前、最后两条素线 SC、SD 的投影 sc、sd 。 作图时，先画出轴线和对称中心的各投影；然后画出底面的各个投影及锥顶点的投影， 再分别画出其外形轮廓线，即完成圆锥的各个投影（见图 6-4c）。 （2）圆锥表面上取点 可根据圆锥面的形成特性来作图。如图 6-4c 所示，己知圆锥 面上点Ｍ的正面投影 m，可采用下列两种方法求出点 M 的水平投影 m 和侧面投影 m。 方法一：辅助素线法 过锥顶 S 和点 M 作一辅助线 SI，根据已知条件可以确定 SI 的 正面投影 s1，然后求出它的水平投影 s1、侧面投影 s1，再由 m根据点在直线上的 投影性质求出 m 和 m。 方法二：辅助圆法 过点 M 作一平行于底面的水平辅助圆，该圆的正面投影为过 m 且平行于 ab的直线 23，它的水平投影为一直径等于 23的圆，m 必在此圆周上，由 m求出 m，再由 m、 m 求出 m。 3.球 球的表面是球面。球面是一个圆母线绕其过圆心且在同一平面上的轴线回转而 形成的（图 6-5a）。 （1）球的投影 如图 6-5b 所示，球的三个投影均为圆，其直径与球直径相等，但三 个投影面上的圆是不同的转向线的投影，正面投影上的圆是平行于 V 面的最大圆的投影 （区分前、后半球表面的外形轮廓线），水平投影上的圆是平行于 H 面的最大圆的投影（区 分上、下半球表面的外形轮廓线），侧面投影上的圆是平行于 W 面的最大圆的投影（区别 左、右半球表面的外形轮廓线）。 作图时，可先画出确定球心的三个投影，再以球心为圆心画出三个与圆球直径相等的 圆。 （2）球面上取点 如图 6-5c 所示，已知球面上点 M 的水平投影 m，要求出其 m和 m。可过点 M 作一平行于 V 面的辅助圆，它的水平投影为 12，正面投影为直径等于 12 的圆，m必定在该圆上，由 m 可求得 m，由 m 和 m可求出 m。显然，点 M 在前半球 面上，因此从前向后看是可见的，同理，点 M 在左半球面上，从左向右看也是可见的。 当然，也可作平行于 H 面的辅助圆来作图，读者自行分析并想像当点位于后半球时， O O C B A 1 m e o 2 d m 1 o 2 f o m a） b） c） 图 6-5 球的投影及表面取点 H V W

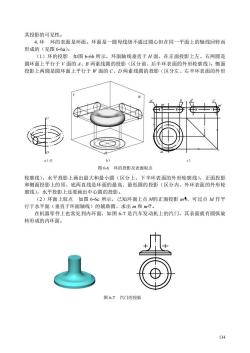
其投影的可见性 4.环环的表面是环面。环面是一圆母线绕不通过圆心但在同一平面上的轴线回转而 形成的（见图6-6a)。 (1)环的投影 如图66b所示，环面轴线垂直于H面，在正面投影上左、右两圆是 圆环面上平行于V面的A、B两素线圆的投影（区分前、后半环表面的外形轮廓线），侧面 投影上两圆是圆环面上平行于W面的C、D两素线圆的投影（区分左、右半环表面的外形 c) 图6-6环的投影及表面取点 轮廓线)，水平投影上画出最大和最小圆（区分上、下半环表面的外形轮廓线），正面投影 和侧面投影上的顶、底两直线是环面的最高、最低圆的投影（区分内、外环表面的外形轮 廓线)，水平投影上还要画出中心圆的投影。 (2)环面上取点如图6-6c所示，己知环面上点M的正面投影m1,可过点M作平 行于水平面（垂直于环面轴线）的辅助圆，求出m和m。 在机器零件上也常见到内环面，如图67是汽车发动机上的汽门，其表面就有圆弧旋 转形成的内环面。 图67汽门的投影

134 其投影的可见性。 4.环 环的表面是环面。环面是一圆母线绕不通过圆心但在同一平面上的轴线回转而 形成的（见图 6-6a）。 （1）环的投影 如图 6-6b 所示，环面轴线垂直于 H 面，在正面投影上左、右两圆是 圆环面上平行于 V 面的 A、B 两素线圆的投影（区分前、后半环表面的外形轮廓线），侧面 投影上两圆是圆环面上平行于 W 面的 C、D 两素线圆的投影（区分左、右半环表面的外形 轮廓线），水平投影上画出最大和最小圆（区分上、下半环表面的外形轮廓线），正面投影 和侧面投影上的顶、底两直线是环面的最高、最低圆的投影（区分内、外环表面的外形轮 廓线），水平投影上还要画出中心圆的投影。 （2）环面上取点 如图 6-6c 所示，己知环面上点Ｍ的正面投影 m，可过点 M 作平 行于水平面（垂直于环面轴线）的辅助圆，求出 m 和 m。 在机器零件上也常见到内环面，如图 6-7 是汽车发动机上的汽门，其表面就有圆弧旋 转形成的内环面。 O m a m b d c m a）O b） c） 图 6-6 环的投影及表面取点 图 6-7 汽门的投影 H V W

图6-8所示是工程上常见的各种不完整的曲面体，应该熟悉它们的投影 eA合68 本申①① 扫 e) 图68不完整的曲面体 a)圆维台b)半圆柱c)半球d)半圆简e)鼓形回转体)四分之一圆环面 6.2平面与立体相交 在工程上常常会遇到平面与立体相交的情形。例如，车刀的刀头是由一个四棱柱被四 个平面切割而成的（图69）：铣床上的尾座顶尖，是由两回转体被平面切割而成的（图 69%)。平面与立体表面相交的交线称为截交线，平面称为截平面。在画图时，为了清楚地 表达它们的形状，必须画出交线的投影。本节将讨论交线的作图方法。 图69立体与平面相交 a)车刀 b)顶尖 立体被平面截切时，立体形状和截平面相对位置不同，所形成截交线的形状也不同 135

135 图 6-8 所示是工程上常见的各种不完整的曲面体，应该熟悉它们的投影。 6.2 平面与立体相交 在工程上常常会遇到平面与立体相交的情形。例如，车刀的刀头是由一个四棱柱被四 个平面切割而成的（图 6-9a）；铣床上的尾座顶尖，是由两回转体被平面切割而成的（图 6-9b）。平面与立体表面相交的交线称为截交线，平面称为截平面。在画图时，为了清楚地 表达它们的形状，必须画出交线的投影。本节将讨论交线的作图方法。 立体被平面截切时，立体形状和截平面相对位置不同，所形成截交线的形状也不同。 图 6-8 不完整的曲面体 a）圆锥台 b）半圆柱 c）半球 d）半圆筒 e）鼓形回转体 f）四分之一圆环面 a） b） 图 6-9 立体与平面相交 a）车刀 b）顶尖 a） b） c） d） e） f）

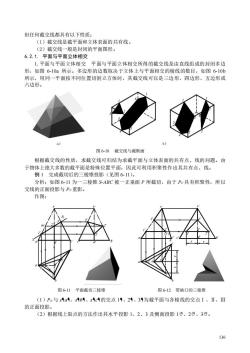
但任何截交线都具有以下性质： (1)截交线是截平面和立体表面的共有线。 (2)截交线一般是封闭的平面图形。 6.2.1.平面与平面立体相交 1.平面与平面立体相交平面与平面立体相交所得的截交线是由直线组成的封闭多边 形，如图6-10a所示。多边形的边数取决于立体上与平面相交的棱线的数目，如图6-10 所示，用同一平面按不同位置切割立方体时，其截交线可以是三边形、四边形、五边形或 六边形。 b) 图610截交线与截断面 根据截交线的性质，求截交线可归结为求截平面与立体表面的共有点、线的问题。由 于物体上绝大多数的截平面是特殊位置平面，因此可利用积聚性作出其共有点、线。 例1完成截切后的三棱锥投影（见图6-11）。 分析：如图6-11为一三棱锥S4BC被一正垂面P所截切，由于P具有积聚性，所以 交线的正面投影与Pr重影。 作图： 图6-11平面截切三棱锥 图6-12带缺口的三棱锥 (1)Pr与s4a4、s4b1、s1c4的交点11、21、34为截平面与各棱线的交点I、Ⅱ、Ⅲ 的正面投影。 (2)根据线上取点的方法作出其水平投影1、2、3及侧面投影1号、2、3 136

136 但任何截交线都具有以下性质： （1）截交线是截平面和立体表面的共有线。 （2）截交线一般是封闭的平面图形。 6.2.1. 平面与平面立体相交 1.平面与平面立体相交 平面与平面立体相交所得的截交线是由直线组成的封闭多边 形，如图 6-10a 所示。多边形的边数取决于立体上与平面相交的棱线的数目，如图 6-10b 所示，用同一平面按不同位置切割立方体时，其截交线可以是三边形、四边形、五边形或 六边形。 根据截交线的性质，求截交线可归结为求截平面与立体表面的共有点、线的问题。由 于物体上绝大多数的截平面是特殊位置平面，因此可利用积聚性作出其共有点、线。 例 1 完成截切后的三棱锥投影（见图 6-11）。 分析：如图 6-11 为一三棱锥 S-ABC 被一正垂面 P 所截切，由于 PV 具有积聚性，所以 交线的正面投影与 PV 重影。 作图： （1）PV 与 sa、sb、sc的交点 1、2、3为截平面与各棱线的交点Ⅰ、Ⅱ、Ⅲ 的正面投影。 （2）根据线上取点的方法作出其水平投影 1、2、3 及侧面投影 1、2、3。 1 2 3 3 4 5 6 1 2 2 2 1 1 3 3 4 4 5 a） b） 图 6-10 截交线与截断面 P X c 3 2 b a m s 1 V s m 2 3 1 a b c c a b 2 1 3 s c 3 a 1 4 s 2 b y y y y a 1 4 s 2 3 b c c a b 2 1 3 4 s ( ) 图 6-11 平面截切三棱锥 图 6-12 带缺口的三棱锥

(3)连接各点的同面投影即得截交线的三个投影。 例2完成带缺口的三棱锥的投影（见图6-12）。 分析：图612为一带切口的三棱锥，切口由水平截面和正垂截面组成，切口的正面投 影有积聚性。水平截面与三棱锥的底面平行，因此它与△SAB棱面的交线IⅡ必平行于底 边AB,与△SMC棱面的交线IⅢ必平行于底边AC,正垂截面分别与△SMB、△SMC棱面 交于ⅡV和ⅢⅣ。由于组成切口的两个截面都垂直于正投影面，所以两截面的交线ⅡⅢ 一定是正垂线，画出这些交线的投影即完成切口的水平投影和侧面投影。 作图： (1)由11在sa上作出1，由12∥ab、13∥ac,再分别由21、34在12和13上作出2、 3。由121和12作出123，由1134和13作出13号。12和13重合在水平截面 的侧面投影上。 (2)由41分别在a和s9上作出4和4，然后再分别与2、3和2、3连成42 43和42、43，即完成切口的水平投影和侧面投影。特别注意组成切口两截面交线 的水平投影23应连成虚线。 2.平面立体被切割，开槽与穿孔平面立体被切割、开槽与穿孔时，随着截切面的位 置不同，变化甚多。以下列举几个在零件中最常见的基本情况。 (1)图6-13a所示四棱柱的前后棱面P均为侧垂面，被水平面R和侧平面Q所切割 先作出切割后的主视图与左视图。水平面R与前、后侧垂面P的交线AB和CD均为侧垂 线，拉先找出其在左视图上的投影 一点a"b“和c”d”,再按宽相等的投影规律，作出交线 在俯视图上的投影ab和cd。 (a) (6) 图6-13四棱柱体被切剖 图6-13b为同样的四棱柱被正垂面S所斜切，由于平面S和P分别在主、左视图上具 有重影性，因此它们的交线AB(一般位置线)在主、左视图上的投影ab'和a"b“分别与 s和p”重影。按投影规律便能作出该交线在俯视图上的投影ab。 如切割的部位从四棱柱的左上方移到中上方，如图6-14a,则习惯上称之为开槽。如 切割部位移到四棱柱的中部，如图6-14b,则习惯上称之为穿孔。其交线的求法与图6-13a 所述基本相同，请读者自行分析。 137

137 （3）连接各点的同面投影即得截交线的三个投影。 例 2 完成带缺口的三棱锥的投影（见图 6-12）。 分析：图 6-12 为一带切口的三棱锥，切口由水平截面和正垂截面组成，切口的正面投 影有积聚性。水平截面与三棱锥的底面平行，因此它与△SAB 棱面的交线ⅠⅡ必平行于底 边 AB，与△SAC 棱面的交线ⅠⅢ必平行于底边 AC，正垂截面分别与△SAB、△SAC 棱面 交于Ⅱ Ⅳ和Ⅲ Ⅳ。由于组成切口的两个截面都垂直于正投影面，所以两截面的交线ⅡⅢ 一定是正垂线，画出这些交线的投影即完成切口的水平投影和侧面投影。 作图： （1）由 1在 sa 上作出 1，由 12∥ab、13∥ac，再分别由 2、3在 12 和 13 上作出 2、 3。由 12和 12 作出 12，由 13和 13 作出 13。12和 13重合在水平截面 的侧面投影上。 （2）由 4分别在 sa 和 sa上作出 4 和 4，然后再分别与 2、3 和 2、3连成 42、 43 和 42、43，即完成切口的水平投影和侧面投影。特别注意组成切口两截面交线 的水平投影 23 应连成虚线。 2．平面立体被切割，开槽与穿孔 平面立体被切割、开槽与穿孔时，随着截切面的位 置不同，变化甚多。以下列举几个在零件中最常见的基本情况。 （1） 图 6-13a 所示四棱柱的前后棱面 P 均为侧垂面，被水平面 R 和侧平面 Q 所切割， 先作出切割后的主视图与左视图。水平面 R 与前、后侧垂面 P 的交线 AB 和 CD 均为侧垂 线，应先找出其在左视图上的投影——点 a"b"和 c"d"，再按宽相等的投影规律，作出交线 在俯视图上的投影 ab 和 cd。 图 6-13b 为同样的四棱柱被正垂面 S 所斜切，由于平面 S 和 P 分别在主、左视图上具 有重影性，因此它们的交线 AB（一般位置线）在主、左视图上的投影 a'b'和 a"b"分别与 s'和 p″重影。按投影规律便能作出该交线在俯视图上的投影 ab。 如切割的部位从四棱柱的左上方移到中上方，如图 6-14a，则习惯上称之为开槽。如 切割部位移到四棱柱的中部，如图 6-l4b，则习惯上称之为穿孔。其交线的求法与图 6-13a 所述基本相同，请读者自行分析。 a b d c q p a'c' d' b' p' q' c"d" a"b" r r" q" p" s a b p a' b' p' s' a" b" s" p" r' （a） （b） 图 6-13 四棱柱体被切割

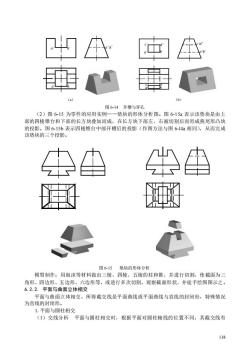
(a) 图6-14开槽与穿孔 (2)图6-15为零件的应用实例一一垫块的形体分析图。图6-15a表示该垫块是由上 部的四棱锥台和下部的长方块叠加而成，在长方块下部左、右被切割后而形成燕尾形凸块 的投影。图6-15b表示四棱锥台中部开槽后的投影（作图方法与图6-14妇相同），从而完成 该垫块的三个投摄影。 图6-15垫块的形体分析 模型制作：用泡沫等材料做出三棱、四棱、五棱的柱和锥，并进行切割，使截面为 角形、四边形、五边形、六边形等，或进行多次切割，观察截面形状，并徒手绘图图示之。 6.2.2.平面与曲面立体相交 平面与曲面立体相交，所得截交线是平面曲线或平面曲线与直线的封闭形，特殊情况 为直线的封闭形。 1.平面与圆柱相交 (1)交线分析平面与圆柱相交时，根据平面对圆柱轴线的位置不同，其截交线有 138

138 （2）图 6-15 为零件的应用实例——垫块的形体分析图。图 6-15a 表示该垫块是由上 部的四棱锥台和下部的长方块叠加而成，在长方块下部左、右被切割后而形成燕尾形凸块 的投影。图 6-15b 表示四棱锥台中部开槽后的投影（作图方法与图 6-l4a 相同），从而完成 该垫块的三个投影。 模型制作：用泡沫等材料做出三棱、四棱、五棱的柱和锥，并进行切割，使截面为三 角形、四边形、五边形、六边形等，或进行多次切割，观察截面形状，并徒手绘图图示之。 6.2.2. 平面与曲面立体相交 平面与曲面立体相交，所得截交线是平面曲线或平面曲线与直线的封闭形，特殊情况 为直线的封闭形。 1.平面与圆柱相交 （1）交线分析 平面与圆柱相交时，根据平面对圆柱轴线的位置不同，其截交线有 a b a b a b a b c d a c b d c b d a （a） （b） 图 6-14 开槽与穿孔 图 6-15 垫块的形体分析

三种情形圆、椭圆和两平行直线，见表6-1。 表61平面与圆柱相交的各种情形 截平面位置 轴线垂 与轴线倾斜 与轴线平行 空间形状 支调花表面 两平行直线 (2)应用实例 1)圆柱被与圆柱轴线平行的平面截切图6-16a所示圆柱体的左、右被切割，先作出 切割后的正面投影，再作出水平投影，最后通过水平投影与正面投影求出侧面投影。侧平 面P的水平投影p与圆的交点(b)为截平面P与圆柱面交线AB的水平投影，按投影规律 作出交线AB的侧面投影a”b”,从而完成被切割后的侧面投影。 图6-16b和c分别表示圆柱体被开槽和穿孔，其交线AB的求法与图6-16a所述基本相 同，但必须注意，在侧面投影上的开槽与穿孔部位处，圆柱的外形轮廓线由于开槽和穿孔 而不存在了。 9⊕ 图6-16圆柱体被切制、开槽与穿孔 a)切制b)开槽c)穿孔 图6-17a、b、c分别表示空心圆柱体被切割、开槽和穿孔后的三面投影画法。作图时 应分别作出切割平面与圆柱外表面及内圆柱表面（即圆柱孔）的交线AB及CD的投影 139

139 三种情形圆、椭圆和两平行直线，见表 6-1。 表 6-1 平面与圆柱相交的各种情形 截平面位置 与轴线垂直 与轴线倾斜 与轴线平行 空间形状 与圆柱表面 交线形状 圆 椭圆 两平行直线 （2）应用实例 1）圆柱被与圆柱轴线平行的平面截切 图 6-16a 所示圆柱体的左、右被切割，先作出 切割后的正面投影，再作出水平投影，最后通过水平投影与正面投影求出侧面投影。侧平 面 P 的水平投影 p 与圆的交点 a(b)为截平面 P 与圆柱面交线 AB 的水平投影，按投影规律 作出交线 AB 的侧面投影 a"b"，从而完成被切割后的侧面投影。 图 6-16b 和 c 分别表示圆柱体被开槽和穿孔，其交线 AB 的求法与图 6-16a 所述基本相 同，但必须注意，在侧面投影上的开槽与穿孔部位处，圆柱的外形轮廓线由于开槽和穿孔 而不存在了。 图 6-17a、b、c 分别表示空心圆柱体被切割、开槽和穿孔后的三面投影画法。作图时 应分别作出切割平面与圆柱外表面及内圆柱表面（即圆柱孔）的交线 AB 及 CD 的投影， p a b p b a a b p ( ) a b b a a b ( ) a b b a a b a） b） c） 图 6-16 圆柱体被切割、开槽与穿孔 a）切割 b）开槽 c）穿孔