《画法几何与工程制图》课程教学资源（教材讲义）第05章 轴测投影及其草图速画技术

第7章轴测投影(GB/T4458.3一2006)及其草图速画技术 工程上一般采用多面正投影图绘制图样，如图7-1所示，它可以较完整、确切地表达 出零件各部分的形状，且作图方便。但这种图样直观性差，不具有一定读图能力的人，难 以看懂。为了帮助看图，工程上还采用如图7-1b所示的轴测投影图，它能在一个投影上同 时反映物体的正面、顶面和侧面的形状，因此富有立体感。但零件上原来的长方形平面， 在轴测投影图上变成了平行四边形，圆变成了椭圆，因此不能确切地表达零件原来的形状 与大小，且作图较复杂，因而轴测图在工程上一般仅用作辅助图样。 b) 图71多面正投影图与轴测图的比较 7.1轴测投影的基本原理 1.轴测投影的形成图7-2表明了正投影图和轴测投影图的形成方法。为便于分析， 假想将物体放在一个空间的直角坐标体系中，其坐标轴X、Y、Z和物体上三条互相垂直的 棱线（长、宽、高）重合，O为原点。在图7-2a中，按与投影面P垂直的方向S投射，在f 面上得到它的正投影图。由于S平行于物体的顶面和侧面，也即平行于轴，所得的视图 不能反映顶面和侧面的形状，因而立体感不强。要获得富有立体感的轴测图，必须使投 射方向S不平行于物体上任一坐标面，或将物体绕假象的Z轴、X轴旋转一个角度（图7-2）。 这种将物体连同直角坐标系，按投射方向用平行投影法将其投射在单一投影面上所得的 具有立体感的图形称为轴测投影图，简称轴测图：该投影面称为轴测投影面。通常轴测 投影有以下两种基本形成方法： 159

159 第7章 轴测投影（GB/T 4458.3—2006）及其草图速画技术 工程上一般采用多面正投影图绘制图样，如图7-1a所示，它可以较完整、确切地表达 出零件各部分的形状，且作图方便。但这种图样直观性差，不具有一定读图能力的人，难 以看懂。为了帮助看图，工程上还采用如图7-1b所示的轴测投影图，它能在一个投影上同 时反映物体的正面、顶面和侧面的形状，因此富有立体感。但零件上原来的长方形平面， 在轴测投影图上变成了平行四边形，圆变成了椭圆，因此不能确切地表达零件原来的形状 与大小，且作图较复杂，因而轴测图在工程上一般仅用作辅助图样。 7.1 轴测投影的基本原理 1.轴测投影的形成 图7-2表明了正投影图和轴测投影图的形成方法。为便于分析， 假想将物体放在一个空间的直角坐标体系中，其坐标轴X、Y、Z和物体上三条互相垂直的 棱线（长、宽、高）重合，O为原点。在图7-2a中，按与投影面P垂直的方向S0投射，在P 面上得到它的正投影图。由于S0平行于物体的顶面和侧面，也即平行于Y轴，所得的视图 不能反映顶面和侧面的形状，因而立体感不强。要获得富有立体感的轴测图，必须使投 射方向S不平行于物体上任一坐标面，或将物体绕假象的Z轴、X轴旋转一个角度（图7-2）。 这种将物体连同直角坐标系，按投射方向用平行投影法将其投射在单一投影面上所得的 具有立体感的图形称为轴测投影图，简称轴测图；该投影面称为轴测投影面。通常轴测 投影有以下两种基本形成方法： 图7-1 a） b） 图 7-1 多面正投影图与轴测图的比较

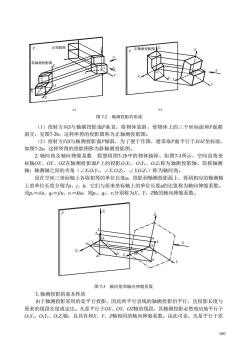
正投影图 。正轴测投影图 油测投影是 b) 图-2轴测投影的形成 (1)投射方向S与轴测投影面P垂直，将物体放斜，使物体上的三个坐标面和P面都 斜交，见图7-2b,这样所得的投影图称为正轴测投影图。 (2)投射方向S与轴测投影面P倾斜，为了便于作图，通常取P面平行于XOZ坐标面 如图7-2，这样所得的投影图称为斜轴测投影图。 2.轴间角及轴向伸缩系数假想将图7-2b中的物体抽掉，如图73所示，空间直角坐 标轴OX、OY、OZ在轴测投影面P上的投影OX、OX、OZ称为轴测投影轴，简称轴测 轴：轴测轴之间的夹角（∠XOY、∠XOZ1、∠OZ)称为轴间角。 设在空间三坐标轴上各取相等的单位长度山，投影到轴测投影面上，得到相应的轴测轴 上的单位长度分别为、人、k,它们与原来坐标轴上的单位长度的比值称为轴向伸缩系数。 设p=u、q1=ju、n=,则p、q、n分别称为X、X、Z轴的轴向伸缩系数， 图7-3轴间角和轴向伸缩系数 3.轴测投影的基本性质 由于轴测投影采用的是平行投影，因此两平行直线的轴测投影仍平行，且投影长度与 原来的线段长度成定比。凡是平行于OX、OX、OZ轴的线段，其轴测投影必然相应地平行于 OX、OY、OZ轴，且具有和K、Z轴相同的轴向伸缩系数。由此可见，凡是平行于原 160

160 （1）投射方向S与轴测投影面P垂直，将物体放斜，使物体上的三个坐标面和P面都 斜交，见图7-2b，这样所得的投影图称为正轴测投影图。 （2）投射方向S与轴测投影面P倾斜，为了便于作图，通常取P面平行于XOZ坐标面， 如图7-2a，这样所得的投影图称为斜轴测投影图。 2.轴间角及轴向伸缩系数 假想将图7-2b中的物体抽掉，如图7-3所示，空间直角坐 标轴OX、OY、OZ在轴测投影面P上的投影O1X1、O1Y1、O1Z1称为轴测投影轴，简称轴测 轴；轴测轴之间的夹角（∠X1O1Y1、∠X1O1Z1、∠Y1O1Z1）称为轴间角。 设在空间三坐标轴上各取相等的单位长度u，投影到轴测投影面上，得到相应的轴测轴 上的单位长度分别为i、j、k，它们与原来坐标轴上的单位长度u的比值称为轴向伸缩系数。 设p1＝i/u、q1＝j/u、r1＝k/u，则p1、q1、r1分别称为X、Y、Z轴的轴向伸缩系数。 3.轴测投影的基本性质 由于轴测投影采用的是平行投影，因此两平行直线的轴测投影仍平行，且投影长度与 原来的线段长度成定比。凡是平行于OX、OY、OZ轴的线段，其轴测投影必然相应地平行于 O1X1、O1Y1、O1Z1轴，且具有和X、Y、Z轴相同的轴向伸缩系数。由此可见，凡是平行于原 P Z X Y O S S Z X Y 1 0 O1 Z Y S Z X Y O X P 1 1 1 O1 1 1 正投影图 斜轴测投影图 正轴测投影图 a） b） 图 7-2 轴测投影的形成 Z Y S Z X Y O X P 1 1 1 u k i j a a a a 1 X 1 X 1 O A A u u 1 图 7-3 轴间角和轴向伸缩系数

坐标轴的线段长度乘以相应的轴向伸缩系数，就是该线段的轴测投影长度，也就是，在轴 测图中只有沿轴测轴方向测量的长度才与原坐标轴方向的长度有一定的对应关系，轴测投 影由此而得名。在图7-3中空间A点的轴测投影为A,其中Oan=prOax:ana=qraa(由于 aa∥OY,所以anallO.Y)a4=nra4(由于aA∥OZ,所以a4llOZ) 4.轴测投影的分类根据投射方向和轴测投影面的相对关系，轴测投影图可分为正轴 测投影图和斜轴测投影图两类。根据轴向伸缩系数的不同，各类又可分为三种： (1)如p=q=n,称为正（或斜）等轴测图。 (2)如p=q≠n或p1≠q=n或p=n≠g,称为正（或斜）二轴测图。 (3)如p≠q≠n,称为正（或斜）三轴测图。 在实际作图时，正等轴测图用得较多：对于正二轴测图及斜二轴测图，一般采用的轴向 伸缩系数为p=n、g=Pm2。其余各种轴测投影，可视作图时的具体要求选用，但一般需采 用专用工具，否则其作图甚繁。本章仅介绍正等轴测图和斜二轴测图两种轴测图的画法。 7.2正轴测图 1.正轴测图的轴间角和轴向伸缩系数 (1)正等轴测图根据理论分析（证明从略，请参阅轴测投影学），正等轴测图的投射 方向的水平投影和正面投影均为45°，轴间角为∠X0Y=∠X0乙=∠Z0Y=120°，如 图74所示：作图时，一般使O,Z轴处于垂直位置，则0X和O,Y轴与水平线成30°，可 利用30°三角板方便地作出（图7-4b)。正等轴测图的轴向伸缩系数p1=q1=n≈0.82。但在 实际作图时，按上述轴向伸缩系数计算尺寸相当麻烦。而绘制轴测图的主要目的是为了表达 物体的直观形状，故为了作图方便，常采用一组简化伸缩系数P、4、人使p:g:一m:q心 :n。简化伸缩系数之比值，即p:g:r应采用简单的数值，在正等轴测图中，取p=q=r =1,因此就可以将视图上的尺寸a、b和h直接度量到相应的X、Y,和Z轴上，这样作出长 方块的正等轴测图其形状不变，仅图形按一定比例放大，图上线段的放大倍数为10.82≈1.22 倍。图74c所示为长方块的长、宽和高分别为a、b和h,按上述轴间角和轴向伸缩系数作 出的正等轴测图。 :=49入 =g=r=Q82 面投影图 a)投射方向 )轴间角与轴向仲缩系数 ©)长方体轴向伸缩系数理论值和简化值的区别 图74正等轴测图的轴间角与轴向伸缩系数 (2)正二轴测图正二轴测图的轴间角与轴向伸缩系数及作图等如图7-5所示，叙述从 6

161 坐标轴的线段长度乘以相应的轴向伸缩系数，就是该线段的轴测投影长度，也就是，在轴 测图中只有沿轴测轴方向测量的长度才与原坐标轴方向的长度有一定的对应关系，轴测投 影由此而得名。在图7-3中空间A点的轴测投影为A1，其中O1aX1＝p1∙OaX；aX1a1＝q1∙aXa（由于 aXa∥OY，所以aX1a1//O1Y1）；a1A1＝r1∙aA（由于aA∥OZ，所以a1A1//O1Z1）。 4.轴测投影的分类 根据投射方向和轴测投影面的相对关系，轴测投影图可分为正轴 测投影图和斜轴测投影图两类。根据轴向伸缩系数的不同，各类又可分为三种： （1）如 p1＝q1＝r1，称为正（或斜）等轴测图。 （2）如 p1＝q1≠r1或 p1≠q1＝r1或 p1＝r1≠q1，称为正（或斜）二轴测图。 （3）如 p1≠q1≠r1，称为正（或斜）三轴测图。 在实际作图时，正等轴测图用得较多；对于正二轴测图及斜二轴测图，一般采用的轴向 伸缩系数为 p1＝r1、q1＝p1/2。其余各种轴测投影，可视作图时的具体要求选用，但一般需采 用专用工具，否则其作图甚繁。本章仅介绍正等轴测图和斜二轴测图两种轴测图的画法。 7.2 正轴测图 1.正轴测图的轴间角和轴向伸缩系数 （1）正等轴测图 根据理论分析（证明从略，请参阅轴测投影学），正等轴测图的投射 方向的水平投影和正面投影均为 45°，轴间角为∠X1O1Y1＝∠X1O1Z1＝∠Z1O1Y1＝120°，如 图 7-4 所示；作图时，一般使 O1Z1轴处于垂直位置，则 O1X1和 O1Y1轴与水平线成 30°，可 利用 30°三角板方便地作出（图 7-4b）。正等轴测图的轴向伸缩系数 p1＝q1＝r1≈0.82。但在 实际作图时，按上述轴向伸缩系数计算尺寸相当麻烦。而绘制轴测图的主要目的是为了表达 物体的直观形状，故为了作图方便，常采用一组简化伸缩系数 p、q、r，使 p﹕q﹕r＝p1﹕q1 ﹕r1。简化伸缩系数之比值，即 p﹕q﹕r 应采用简单的数值，在正等轴测图中，取 p＝q＝r ＝1，因此就可以将视图上的尺寸 a、b 和 h 直接度量到相应的 X1、Y1和 Z1轴上，这样作出长 方块的正等轴测图其形状不变，仅图形按一定比例放大，图上线段的放大倍数为 1/0.82≈1.22 倍。图 7-4c 所示为长方块的长、宽和高分别为 a、b 和 h，按上述轴间角和轴向伸缩系数作 出的正等轴测图。 p＝q＝r＝0.82 p＝q＝r＝1 r＝0.82 q＝0.82 p＝0.82 ε1＝45° ε2＝45° 图7-4 b a h 1 1 1 1 30° 30° Y 120° Z 120° 120° X O 两面投影图 a）投射方向 b）轴间角与轴向伸缩系数 c）长方体轴向伸缩系数理论值和简化值的区别 图 7-4 正等轴测图的轴间角与轴向伸缩系数 （2）正二轴测图 正二轴测图的轴间角与轴向伸缩系数及作图等如图 7-5 所示，叙述从 略

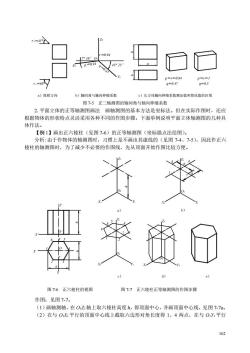
2457 7°0 p0. ,=60 =07 8)投射方向 b)轴间角与轴向伸缩系数 ©)长方体轴向伸缩系数理论值和筒化值的区别 图75正二轴测图的轴间角与轴向伸缩系数 2.平面立体的正等轴测图画法画轴测图的基本方法是坐标法。但在实际作图时，还应 根据物体的形状特点灵活采用各种不同的作图步骤。下面举例说明平面立体轴测图的几种具 体作法。 【例1】画出正六棱柱（见图7-6）的正等轴测图（坐标描点法绘图） 分析：由于作物体的轴测图时，习惯上是不画出其虚线的（见图74、75），因此作正六 棱柱的轴测图时，为了减少不必要的作图线，先从顶面开始作图比较方便。 图7-6正六棱柱的视图 图77正六棱柱正等轴测图的作图步骤 作图：见图7-7。 (1)画轴测轴，在OZ轴上取六棱柱高度h,得项面中心，并画顶面中心线，见图7-7a。 (2)在与OX平行的顶面中心线上截取六边形对角长度得1、4两点，在与OY平行 162

162 p＝r＝1 q＝0.47 q＝0.5 41°25′ p＝r＝0.94 r＝0.94 q＝0.47 p＝0.94 ε1＝69° ε2＝45° 图7-5 b a h 1 1 1 1 7°10′ Y Z X O a）投射方向 b）轴间角与轴向伸缩系数 c）长方体轴向伸缩系数理论值和简化值的区别 图 7-5 正二轴测图的轴间角与轴向伸缩系数 2.平面立体的正等轴测图画法 画轴测图的基本方法是坐标法。但在实际作图时，还应 根据物体的形状特点灵活采用各种不同的作图步骤。下面举例说明平面立体轴测图的几种具 体作法。 【例 1】画出正六棱柱（见图 7-6）的正等轴测图（坐标描点法绘图）。 分析:由于作物体的轴测图时，习惯上是不画出其虚线的（见图 7-4、7-5），因此作正六 棱柱的轴测图时，为了减少不必要的作图线，先从顶面开始作图比较方便。 作图：见图 7-7。 （1）画轴测轴，在 O1Z1轴上取六棱柱高度 h，得顶面中心，并画顶面中心线，见图 7-7a。 （2）在与 O1X1平行的顶面中心线上截取六边形对角长度得 1、4 两点，在与 O1Y1平行 Z X Y 1 O 2 3 4 6 5 7 8 b h a Z X O Y h Z X Y O 1 8 4 7 b a X Y O Z Z X Y O 1 2 3 4 5 6 7 8 X O 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 图 7-6 正六棱柱的视图 图 7-7 正六棱柱正等轴测图的作图步骤 a） c） d） e） b）

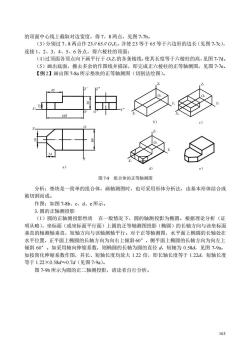
的顶面中心线上截取对边宽度，得7、8两点，见图77b。 (3)分别过7、8两点作23∥65∥0X,并使23等于65等于六边形的边长（见图7-7C), 连接1、2、3、4、5、6各点，得六棱柱的顶面： (4)过顶面各顶点向下画平行于OZ的各条棱线，使其长度等于六棱柱的高，见图7-7d (5)画出底面，擦去多余的作图线并描深，即完成正六棱柱的正等轴测图，见图7-7。 【例2】画出图7-8a所示垫块的正等轴测图（切割法绘图）。 e) 图7-8组合体的正等轴测图 分析：垫块是一简单的组合体，画轴测图时，也可采用形体分析法，由基本形体结合或 被切割而成。 作图：如图7-8b、c、d、e所示。 3.圆的正轴测投影 (1)圆的正轴测投影性质在一般情况下，圆的轴测投影为椭圆。根据理论分析（证 明从略)，坐标面（或坐标面平行面）上圆的正等轴测图投影（椭圆）的长轴方向与该坐标面 垂直的轴测轴垂直，短轴方向与该轴测轴平行。对于正等轴测图，水平面上椭圆的长轴处在 水平位置，正平面上椭圆的长轴方向为向右上倾斜60°，侧平面上椭圆的长轴方向为向左上 倾斜60°。如采用轴向伸缩系数，则椭圆的长轴为圆的直径d,短轴为0.58d,见图7-9a 如按简化伸缩系数作图，其长、短轴长度均放大1.22倍，即长轴长度等于1.22d,短轴长度 等千122X058d≈07d(见图7.9a)。 图7-9b所示为圆的正二轴测投影，请读者自行分析

163 的顶面中心线上截取对边宽度，得 7、8 两点，见图 7-7b。 （3）分别过 7、8 两点作 23∥65∥O1X1，并使 23 等于 65 等于六边形的边长（见图 7-7c）， 连接 1、2、3、4、5、6 各点，得六棱柱的顶面； （4）过顶面各顶点向下画平行于 O1Z1的各条棱线，使其长度等于六棱柱的高，见图 7-7d。 （5）画出底面，擦去多余的作图线并描深，即完成正六棱柱的正等轴测图，见图 7-7e。 【例 2】画出图 7-8a 所示垫块的正等轴测图（切割法绘图）。 分析：垫块是一简单的组合体，画轴测图时，也可采用形体分析法，由基本形体结合或 被切割而成。 作图：如图 7-8b、c、d、e 所示。 3.圆的正轴测投影 （1）圆的正轴测投影性质 在一般情况下，圆的轴测投影为椭圆。根据理论分析（证 明从略），坐标面（或坐标面平行面）上圆的正等轴测图投影（椭圆）的长轴方向与该坐标面 垂直的轴测轴垂直，短轴方向与该轴测轴平行。对于正等轴测图，水平面上椭圆的长轴处在 水平位置，正平面上椭圆的长轴方向为向右上倾斜 60°，侧平面上椭圆的长轴方向为向左上 倾斜 60°。如采用轴向伸缩系数，则椭圆的长轴为圆的直径 d，短轴为 0.58d，见图 7-9a。 如按简化伸缩系数作图，其长、短轴长度均放大 1.22 倍，即长轴长度等于 1.22d，短轴长度 等于 1.22×0.58d≈0.7d（见图 7-9a）。 图 7-9b 所示为圆的正二轴测投影，请读者自行分析。 X Y Z O X X Z Z Y Y O X Z Y Z O X Y 45 105 38 15 18 60 24 ″ O O O″ ″ 1 1 1 1 1 1 1 1 1 1 1 1 图 7-8 组合体的正等轴测图 a） b） c） d） e）

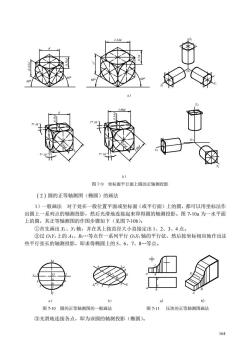
b) 图7-9坐标面平行面上圆的正轴测投影 (2)圆的正等轴测图（椭圆）的画法 1)一般画法对于处在一般位置平面或坐标面（或平行面）上的圆，都可以用坐标法作 出圆上一系列点的轴测投影，然后光滑地连接起来即得圆的轴测投影。图7-10妇为一水平面 上的圆，其正等轴测图的作图步骤如下（见图7-10b): ①首先画出X、Y轴，并在其上按直径大小直接定出1、2、3、4点。 ②过O1Y上的A1、B.等点作一系列平行O1X轴的平行弦，然后按坐标相应地作出这 些平行弦长的轴测投影，即求得椭圆上的5、6、7、8.等点。 图7-10圆的正等轴测图的一般画法 图7-11压块的正等轴测图画法 ③光滑地连接各点，即为该圆的轴测投影（椭圆）。 164

164 1 1 1 1 O Y X Z 1.22d 0.7d d 0.58d 60° 60° 60° 60° a） 1 O1 Z Y1 X1 1.06d 0.34d 7°10′ 0.93d 7°10′ d 1.06d 0.88d 0.33d d 7°10′ 7°10′ 图7-9b b） 图 7-9 坐标面平行面上圆的正轴测投影 （2）圆的正等轴测图（椭圆）的画法 1）一般画法 对于处在一般位置平面或坐标面（或平行面）上的圆，都可以用坐标法作 出圆上一系列点的轴测投影，然后光滑地连接起来即得圆的轴测投影。图 7-10a 为一水平面 上的圆，其正等轴测图的作图步骤如下（见图 7-10b）： ①首先画出 X1、Y1 轴，并在其上按直径大小直接定出 1、2、3、4 点。 ②过 O1Y1 上的 A1、B1.等点作一系列平行 O1X1 轴的平行弦，然后按坐标相应地作出这 些平行弦长的轴测投影，即求得椭圆上的 5、6、7、8.等点。 ③光滑地连接各点，即为该圆的轴测投影（椭圆）。 X Y 1 2 3 4 5 6 7 8 a b O X Y O A B 1 2 3 4 5 6 7 8 1 1 1 1 1 d a b c a c d b D C B A a） b） a） b） 图 7-10 圆的正等轴测图的一般画法 图 7-11 压块的正等轴测图画法

图7-11a为一压块，其前面的圆弧连接部分，也同样可利用一系列Z轴的平行线（如BC), 并按相应的坐标作出各点的轴测投影，光滑地连接后即完成前表面的正等轴测图（图7-11b) 再过各点（如点C)作y轴平行线，并量取宽度，得到后表面上的各点（如点D),从而完成 压块的正等轴测图。 2)近似画法为了简化作图，轴测投影中的椭圆通常采用近似画法。图712表示直径 为d的圆在正等轴测图中XOY面上椭圆的画法，具体作图步骤如下： ①首先通过椭圆中心O作X、Y轴，并按直径d在轴上量取点A1、B1、C、D,(见图 7-12a) ②过点A1、B、C、D分别作Y1轴与X轴的平行线，所形成的菱形即为已知圆的外切 正方形的轴测投影，而所作的椭圆则必然内切于该菱形。该菱形的对角线即为长、短轴的位 置（见图7-12b)。 ③分别以点1、3为圆心，以1B1或3A1为半径作两个大圆弧B1D,和A1C,，连接1D1 1B1,与长轴相交于2、4两点，即为两个小圆弧的中心（见图7-12c) ④以点2、4为圆心，以2D1或4B1为半径作两个小圆弧与大圆弧相接，即完成该椭圆 (见图7-12d)。显然，点A、B1、C、D正好是大、小圆弧的切点。 XO1Z和Y1OZ面上的椭圆，仅长、短轴的方向不同，其画法与在XOY1面上的椭圆 完全相同。 b) 图7-12正等轴测图椭圆的近似画法 4.曲面立体的正等轴测图画法掌握了圆的正等轴测图的画法后，就不难画出回转曲面 立体的正等轴测图。图7-13所示为圆柱正等轴测图画法。作图时，先分别作出其顶面和底面 的椭圆，再作其公切线即成。 b) 图7-13圆柱正等轴测图的画法 165

165 图 7-11a 为一压块，其前面的圆弧连接部分，也同样可利用一系列 Z 轴的平行线（如 BC）， 并按相应的坐标作出各点的轴测投影，光滑地连接后即完成前表面的正等轴测图（图 7-11b）； 再过各点（如点 C）作 y 轴平行线，并量取宽度，得到后表面上的各点（如点 D），从而完成 压块的正等轴测图。 2）近似画法 为了简化作图，轴测投影中的椭圆通常采用近似画法。图 7-12 表示直径 为 d 的圆在正等轴测图中 X1O1Y1 面上椭圆的画法，具体作图步骤如下： ①首先通过椭圆中心 O1 作 X1、Y1 轴，并按直径 d 在轴上量取点 A1、B1、C1、D1（见图 7-12a）。 ②过点 A1、B1、C1、D1 分别作 Y1 轴与 X1 轴的平行线，所形成的菱形即为已知圆的外切 正方形的轴测投影，而所作的椭圆则必然内切于该菱形。该菱形的对角线即为长、短轴的位 置（见图 7-12b）。 ③分别以点 1、3 为圆心，以 1B1 或 3A1 为半径作两个大圆弧 B1D1 和 A1C1 ，连接 1D1、 1B1，与长轴相交于 2、4 两点，即为两个小圆弧的中心（见图 7-12c）。 ④以点 2、4 为圆心，以 2D1 或 4B1 为半径作两个小圆弧与大圆弧相接，即完成该椭圆 （见图 7-12d）。显然，点 A1、B1、C1、D1 正好是大、小圆弧的切点。 X1O1Z1 和 Y1O1Z1 面上的椭圆，仅长、短轴的方向不同，其画法与在 X1O1Y1 面上的椭圆 完全相同。 4.曲面立体的正等轴测图画法 掌握了圆的正等轴测图的画法后，就不难画出回转曲面 立体的正等轴测图。图 7-13 所示为圆柱正等轴测图画法。作图时，先分别作出其顶面和底面 的椭圆，再作其公切线即成。 X O Y Z1 1 1 1 a) b) c) 图 7-13 圆柱正等轴测图的画法 d d A C D B X Y O X Y A C D B O A D C O B 2 1 4 3 D 3 B 4 2 A 1 C 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 O1 a） b） c） d） 图 7-12 正等轴测图椭圆的近似画法

下面举例说明不同形状特点的曲面立体轴测图的具 体作法。 【例3】作支座（图7-14）的正等轴测图（叠加法 绘图) ▣+田 分析·古座由带圆角的矩形底板和上方为半圆形的 竖板所组成，左右对称。先假定将竖板上的半圆形及圆 孔均改为它们的外切正方形，然后再在方形部分的正等 轴测图一一菱形内，根据图7-12所述方法，作出它的内 泡 切椭圆。 作图：如图7-15所示。 (1)画轴测轴，采用简化伸缩系数作图，首先作出 图7-14支座的视图 底板和竖板的外切长方体，注意保持其相对位置（见图7-15a (2)画底板上两个圆柱孔，作出上表面两椭圆中心，画出椭圆，再画出孔的下部椭圆（可 见部分)，见图7-15b。 e) 图715支座的正等轴测图作图步骤 a)叠加b)底板穿孔c)切圆角d)竖板穿孔e)描深 (3)画底板的圆角部分，由于只有1/4圆周，因此作图时可以简化，不必作出整个椭圆 的外切菱形，在角上分别沿轴向取一段等于半径R的线段，得点A1、B与C、D:过以上 各点分别作相应边的垂线，分别交于O1及O2点（图7-15c):以O1及O2为圆心，以O41及 O2C1为半径作弧，即为底板项面上圆角的轴测图。 (4)画立板圆孔（图7-15d)。 166

166 下面举例说明不同形状特点的曲面立体轴测图的具 体作法。 【例 3】作支座（图 7-14）的正等轴测图（叠加法 绘图）。 分析:支座由带圆角的矩形底板和上方为半圆形的 竖板所组成，左右对称。先假定将竖板上的半圆形及圆 孔均改为它们的外切正方形，然后再在方形部分的正等 轴测图——菱形内，根据图 7-12 所述方法，作出它的内 切椭圆。 作图:如图 7-15 所示。 （1）画轴测轴，采用简化伸缩系数作图，首先作出 图 7-14 支座的视图 底板和竖板的外切长方体，注意保持其相对位置（见图 7-15a）。 （2）画底板上两个圆柱孔，作出上表面两椭圆中心，画出椭圆，再画出孔的下部椭圆（可 见部分），见图 7-15b。 （3）画底板的圆角部分，由于只有 1/4 圆周，因此作图时可以简化，不必作出整个椭圆 的外切菱形，在角上分别沿轴向取一段等于半径 R 的线段，得点 A1、B1与 C1、D1；过以上 各点分别作相应边的垂线，分别交于 O1及 O2点（图 7-15c）；以 O1 及 O2为圆心，以 O1A1 及 O2C1 为半径作弧，即为底板顶面上圆角的轴测图。 （4）画立板圆孔（图 7-15d）。 1 1 1 1 2 1 D C A B O O 图 7-15 支座的正等轴测图作图步骤 a）叠加 b）底板穿孔 c）切圆角 d）竖板穿孔 e）描深 a） b） c） d） e） Z X O O Y X

(5)画立板上部半圆柱（图7-15d)。 (6)擦去多余的作图线并描深，即完成支座的正等轴测图（图7-15） 【例4】作托架（图7-16）的正等轴测图。 分析：与例3的情况相同，先作出它的方形轮廓，然后 分别作出上部的半圆槽和下面的长圆形孔。 作图：如图7-17所示。 (1)画轴测轴，采用简化伸缩系数作图，首先作出成L 形的托架的外形轮廊（图7-17a)。 (2)在竖板的前表面上和底板的顶面上分别作出半圆槽 和长圆形孔的轮常（图7-17b)。 (3)将半圆槽的轮廓沿X轴方向向后移一个竖板的宽 图7-16托架的视图 度，将长圆形孔的轮廓沿Z轴方向下移一个底板的厚度（图7-17c)。 (4)擦去多余的作图线并描深，即完成托架的正等轴测图（图7-17d、e) 图7-17托架的正等轴测图作图步骤 a)叠加b)穿孔、挖情c)穿孔、挖槽d)补漏线e)描深 【例5】画出图7-18a所示圆柱被截切后的正等轴测图。 作图步骤（图7-18b、c): (1)画轴测轴，采用简化伸缩系数作图，首先画成完整的圆柱。 (2)在圆柱的轴测图上，定出截平面P的位置，得到所截矩形ABCD

167 （5）画立板上部半圆柱（图 7-15d）。 （6）擦去多余的作图线并描深，即完成支座的正等轴测图（图 7-15e）。 【例 4】作托架（图 7-16）的正等轴测图。 分析：与例 3 的情况相同，先作出它的方形轮廓，然后 分别作出上部的半圆槽和下面的长圆形孔。 作图：如图 7-17 所示。 （1）画轴测轴，采用简化伸缩系数作图，首先作出成 L 形的托架的外形轮廓（图 7-17a）。 （2）在竖板的前表面上和底板的顶面上分别作出半圆槽 和长圆形孔的轮廓（图 7-17b）。 （3）将半圆槽的轮廓沿 X 轴方向向后移一个竖板的宽 度，将长圆形孔的轮廓沿 Z 轴方向下移一个底板的厚度（图 7-17c）。 （4）擦去多余的作图线并描深，即完成托架的正等轴测图（图 7-17d、e）。 【例 5】画出图 7-18a 所示圆柱被截切后的正等轴测图。 作图步骤（图 7-18b、c）: （1）画轴测轴，采用简化伸缩系数作图，首先画成完整的圆柱。 （2）在圆柱的轴测图上，定出截平面 P 的位置，得到所截矩形 ABCD。 图 7-17 托架的正等轴测图作图步骤 a）叠加 b）穿孔、挖槽 c）穿孔、挖槽 d）补漏线 e）描深 a） b） c） d） e） O O X Z X 图 7-16 托架的视图

b c) 图718截切后圆柱的正等轴测图画法 (3)按坐标关系定出C、H、K、E、F、G、D各点，光滑连接成部分椭圆 (4)去掉作图线及不可见线，加深可见轮廓线后，即为所求轴测图。 【例6】画出图7-19妇所示两相交圆柱的正等轴测图。 作图步骤（图7-19b)如下： (1)画出轴测轴，采用简化伸缩系数作图，将两个圆柱按正投影图所给定的相对位置画 出轴测图。 (2)用辅助面法求作轴测图上的相贯线，首先在正投影图中作一系列辅助面，然后在轴 测图上作出相应的辅助面，分别得到辅助交线，辅助交线的交点即为相贯线上的点，连接各 点即为相贯线。 (3)去掉作图线，加深，完成全图 图7-19相交两圆柱的正等轴测图画法 7.3斜二轴测图 1.斜二轴测图的轴间角和轴向伸缩系数从图7-2a可看出，在斜轴测投影中通常将物体 放正，即使XO坐标平面平行于轴测投影面P,因而XO2坐标面或其平行面上的任何图形 在P面上的投影都反映实形，称为正面斜轴测投影。最常用的一种为正面斜二轴测图（简称 斜二轴测图)，其轴间角∠XOZ=90°， ∠X0Y1=∠Y0Z=135°，轴向伸缩系数p1 n=1,q1=0.5。作图时，一般使OZ轴处于垂直位置，则O1X轴为水平线，OY轴与水平 168

168 X X Z Y Z X Y B C A D E F K G H e f k g h a d b c O O c h b k e f g a d a） b） c） 图 7-18 截切后圆柱的正等轴测图画法 （3）按坐标关系定出 C、H、K、E、F、G、D 各点，光滑连接成部分椭圆。 （4）去掉作图线及不可见线，加深可见轮廓线后，即为所求轴测图。 【例 6】画出图 7-19a 所示两相交圆柱的正等轴测图。 作图步骤（图 7-19b）如下: （1）画出轴测轴，采用简化伸缩系数作图，将两个圆柱按正投影图所给定的相对位置画 出轴测图。 （2）用辅助面法求作轴测图上的相贯线，首先在正投影图中作一系列辅助面，然后在轴 测图上作出相应的辅助面，分别得到辅助交线，辅助交线的交点即为相贯线上的点，连接各 点即为相贯线。 （3）去掉作图线，加深，完成全图。 X X O O Y O Y Z Z Z X Y O a） b） 图 7-19 相交两圆柱的正等轴测图画法 7.3 斜二轴测图 1.斜二轴测图的轴间角和轴向伸缩系数 从图 7-2a 可看出，在斜轴测投影中通常将物体 放正，即使 XOZ 坐标平面平行于轴测投影面 P，因而 XOZ 坐标面或其平行面上的任何图形 在 P 面上的投影都反映实形，称为正面斜轴测投影。最常用的一种为正面斜二轴测图（简称 斜二轴测图），其轴间角∠X1O1Z1＝90°，∠X1O1Y1＝∠Y1O1Z1＝135°，轴向伸缩系数 p1＝ r1＝1，q1＝0.5。作图时，一般使 O1Z1 轴处于垂直位置，则 O1X1 轴为水平线，O1Y1 轴与水平