南京农业大学：《生物统计与田间试验》课程教学资源（PPT课件）第四章 理论分布和抽样分布

第四章 理论分布和抽样分布 第一节事件、概率和随机变量 第二节二项式分布 第三节正态分布 第四节抽样分布

第四章 理论分布和抽样分布 第一节 事件、概率和随机变量 第二节 二项式分布 第三节 正态分布 第四节 抽样分布

第一节事件、概率和随机变量 一、事件和事件发生的概率 二、事件间的关系 三、计算事件概率的法则 四、随机变量

第一节 事件、概率和随机变量 一、事件和事件发生的概率 二、事件间的关系 三、计算事件概率的法则 四、随机变量

一、事件和事件发生的概率 事件-在自然界中一种事物，常存在几种可能出现 的情况，每一种可能出现的情况称为事件。 随机事件(random event)-某特定事件只是可能发生 的几种事件中的一种，这种事件称为随机事件。 概率(probability)-每一个事件出现的可能性称为该事 件的概率。 必然事件一对于一类事件来说，在同一组条件的实 现之下必然要发生的，称为必然事件；其概率为1。 不可能事件对于一类事件来说，在同一组条件的 实现之下必然不发生的，称为不可能事件，其概率为0

一、事件和事件发生的概率 事件 -在自然界中一种事物，常存在几种可能出现 的情况，每一种可能出现的情况称为事件。 随机事件(random event) -某特定事件只是可能发生 的几种事件中的一种，这种事件称为随机事件。 概率(probability) -每一个事件出现的可能性称为该事 件的概率。 必然事件-对于一类事件来说，在同一组条件的实 现之下必然要发生的，称为必然事件；其概率为1。 不可能事件-对于一类事件来说，在同一组条件的 实现之下必然不发生的，称为不可能事件，其概率为0

事件发生的可能性（概率）是在大量的实验中观察得到的， 例如棉田发生盲蝽象为害的情况，并不是所有的棉株都受害， 随着观察的次数增多，我们对棉株受害可能性程度大小的把 握越准确、越稳定。这里将一个调查结果列于表4.1。 表4.1在相同条件下盲蝽象在某棉田危害程度的调查结果 调查株数 25 50 1002005001000 15002000 (m) 受害株数 2 12153372177 351 525704 (@) 棉株受害 频率(aln) 0.400.480.300.330.360.3540.3510.3500.352

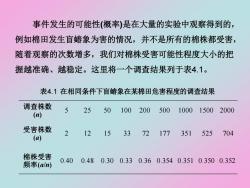
事件发生的可能性(概率)是在大量的实验中观察得到的， 例如棉田发生盲蝽象为害的情况，并不是所有的棉株都受害， 随着观察的次数增多，我们对棉株受害可能性程度大小的把 握越准确、越稳定。这里将一个调查结果列于表4.1。 表4.1 在相同条件下盲蝽象在某棉田危害程度的调查结果 调查株数 (n) 5 25 50 100 200 500 1000 1500 2000 受害株数 (a) 2 12 15 33 72 177 351 525 704 棉株受害 频率(a/n) 0.40 0.48 0.30 0.33 0.36 0.354 0.351 0.350 0.352

由表4.1可以看到：调查5株时，有2株受害，受害株的频 率为40%，调查25株时受害频率为48%，调查100株时受害 频率为33%。可以看出三次调查结果有差异，说明受害频率 有波动、不稳定。而当进一步扩大调查的单株数时，发现频 率比较稳定了，调查500株到2000株的结果是受害棉株稳定 在35%左右。 现以n代表调查株数，以a代表受害株数，那么可以计算 出受害频率p=aln。从棉株受害情况调查结果看，频率在n取 不同的值时，尽管调查田块是相同的，频率却不同，只有 在n很大时频率才比较稳定一致。因而，调查株数n较多时的 稳定频率才能较好地代表棉株受害的可能性

由表4.1可以看到：调查5株时，有2株受害，受害株的频 率为40%，调查25株时受害频率为48%，调查100株时受害 频率为33%。可以看出三次调查结果有差异，说明受害频率 有波动、不稳定。而当进一步扩大调查的单株数时，发现频 率比较稳定了，调查500株到2000株的结果是受害棉株稳定 在35%左右。 现以n代表调查株数，以a代表受害株数，那么可以计算 出受害频率p=a/n。从棉株受害情况调查结果看，频率在n取 不同的值时，尽管调查田块是相同的，频率p却不同，只有 在n很大时频率才比较稳定一致。因而，调查株数n较多时的 稳定频率才能较好地代表棉株受害的可能性

统计学上用n较大时稳定的p近似代表概率。通过大量实 验而估计的概率称为实验概率或统计概率，以表示。此处P代 表概率，P(A)代表事件A的概率，P(A)变化的范围为0~1，即 0sP(A)≤1。 小概率原理-若事件A发生的概率较小，如小于0.05或 0.01,则认为事件A在一次试验中不太可能发生，这称为小 概率事件实际不可能性原理，简称小概率原理。这里的0.05 或0.01称为小概率标准，农业试验研究中通常使用这两个小 概率标准

统计学上用n较大时稳定的p近似代表概率。通过大量实 验而估计的概率称为实验概率或统计概率，以表示。此处P代 表概率，P(A)代表事件A的概率，P(A)变化的范围为0～1，即 0≤P(A)≤1。 小概率原理-若事件A发生的概率较小，如小于0.05或 0.01，则认为事件A在一次试验中不太可能发生，这称为小 概率事件实际不可能性原理，简称小概率原理。这里的0.05 或0.01称为小概率标准，农业试验研究中通常使用这两个小 概率标准

二、事件间的关系 (一)和事件 (二) 积事件 (三)互斥事件 (四)对立事件 (五) 完全事件系 (六)事件的独立性

二、事件间的关系 (一) 和事件 (二) 积事件 (三) 互斥事件 (四) 对立事件 (五) 完全事件系 (六) 事件的独立性

(一）和事件 事件A和B至少有一个发生而构成的新事件称为事件A和 B的和事件，记为A+B,读作“或A发生，或B发生”。 例如，有一批种子，包含有能发芽的和不能发芽的。 若A为“取到能发芽种子”，B为“取到不能发芽种子”， 则A+B为“或者取到能发芽种子或者取到不能发芽种子”。 事件间的和事件可以推广到多个事件：事件A、 A2、A至少有一发生而构成的新事件称为事件A1、 A2、An的和事件，记为A+A2ttAn∑A

(一) 和事件 事件A和B至少有一个发生而构成的新事件称为事件A和 B的和事件，记为A+B，读作“或A发生，或B发生”。 例如，有一批种子，包含有能发芽的和不能发芽的。 若A为“取到能发芽种子”，B为“取到不能发芽种子”， 则A+B为“或者取到能发芽种子或者取到不能发芽种子”。 事件间的和事件可以推广到多个事件：事件A1、 A2、.、An至少有一发生而构成的新事件称为事件A1、 A2、.、An的和事件，记为A1+A2+.+An=  = n i i 1 A

(二)积事件 事件A和B同时发生所构成的新事件称为事件A和B的积 事件，记作AB,读作“A和B同时发生或相继发生”。 事件间的积事件也可以推广到多个事件：事件A、 A2、.、A同时发生所构成的新事件称为这n个事件的积事 件，记作AA2An=1A

(二) 积事件 事件A和B同时发生所构成的新事件称为事件A和B的积 事件，记作AB，读作“A和B同时发生或相继发生”。 事件间的积事件也可以推广到多个事件：事件A1、 A2、.、An同时发生所构成的新事件称为这n个事件的积事 件，记作A1A2.An=  = n i i 1 A

(三)互斥事件 事件A和B不可能同时发生，即AB为不可能事件，记作 AB=V,称事件A和B互斥或互不相容。 例如，有一袋种子，按种皮分黄色和白色。若记A为“取 到黄色”，B为“取到白色”，显然A和B不可能同时发生， 即一粒种子不可能既为黄色又为白色，说明事件A和B互斥。 这一定义也可以推广到n个事件。事件A1、A2、A不 可能同时发生所构成的新事件称为这个事件互斥或互不相容， 记作AA2.An=V

(三) 互斥事件 事件A和B不可能同时发生，即AB为不可能事件，记作 A·B=V，称事件A和B互斥或互不相容。 例如，有一袋种子，按种皮分黄色和白色。若记A为“取 到黄色”，B为“取到白色”，显然A和B不可能同时发生， 即一粒种子不可能既为黄色又为白色，说明事件A和B互斥。 这一定义也可以推广到n个事件。事件A1、A2、.、An不 可能同时发生所构成的新事件称为这n个事件互斥或互不相容， 记作A1·A2.·An=V