南京农业大学：《生物统计与田间试验》课程教学资源（PPT课件）第六章 方差分析

第六章方差分析 第一节方差分析的基本原理 第二节多重比较 第三节方差分析的线性模型与期望均方 第四节单向分组资料的方差分析 第五节两向分组资料的方差分析 第六节方差分析的基本假定和数据转换

第六章 方差分析 第一节 方差分析的基本原理 第二节 多重比较 第三节 方差分析的线性模型与期望均方 第四节 单向分组资料的方差分析 第五节 两向分组资料的方差分析 第六节 方差分析的基本假定和数据转换

第一节方差分析的基本原理 方差是平方和除以自由度的商。 所谓方差分析(analysis of variance),是关于k(k23)个样本 平均数的假设测验方法，是将总变异剖分为各个变异来源的 相应部分，从而发现各变异原因在总变异中相对重要程度的 一种统计分析方法。 假设测验的依据是：扣除了各种试验原因所引起的 变异后的剩余变异提供了试验误差的无偏估计。 这里采用均方来度量试验处理产生的变异和误差引起的 变异

第一节 方差分析的基本原理 所谓方差分析(analysis of variance) ,是关于k(k≥3)个样本 平均数的假设测验方法，是将总变异剖分为各个变异来源的 相应部分，从而发现各变异原因在总变异中相对重要程度的 一种统计分析方法。 假设测验的依据是:扣除了各种试验原因所引起的 变异后的剩余变异提供了试验误差的无偏估计 。 这里采用均方来度量试验处理产生的变异和误差引起的 变异. 方差是平方和除以自由度的商

一、自由度和平方和的分解 设有k组数据，每组皆具n个观察值，则该资料共有nk个观 察值，其数据分组如表6.1。 表6.1每组具n个观察值的k组数据的符号表 组别 观察值(y? i1,2,.,k:j=1,2.,n总和 平均均方 y11 y12 y . yin T 1 s 2 y21 y22 y2j y2n T2 2 : i Vn Vi2 y闭 yin Ti 。 : k yk yk2 y yk知 Tk k T=∑y=∑y

一、自由度和平方和的分解 设有k组数据，每组皆具n个观察值，则该资料共有nk个观 察值，其数据分组如表6.1。 表6.1 每组具n个观察值的k 组数据的符号表 组别 观察值 ( yij，i=1，2，.，k；j=1,2.，n) 总和 平均 均方 1 y11 y12 . y1j . y1n T1 2 y21 y22 . y2j . y2n T2 . . i yi1 yi2 . yij . yin Ti . . k yk1 yk2 . ykj . ykn Tk         T =  y =  y ij     1 y 2 y i y k y y   2 1 s 2 2 s 2 i s   2 k s

在表6.1中，总变异是nk个观察值的变异，故其自由度 v=nk一1，而其平方和SS则为： 5S,=克0y,-列2=空听-C (61) 其中的C称为矫正数： C=②以2T2 (62) nk nk 对于第i组的变异，有 三0，-=2，-男+g-列 20-+220-+20-明 =2,-)广+0-

在表6.1中，总变异是nk个观察值的变异，故其自由度 v = nk－1，而其平方和SST则为： =  − =  − n k n k SST yi j y yi j C 1 1 2 2 ( ) （6·1） 其中的C称为矫正数： nk T nk y C 2 2 =  = ( ) (6·2) 对于第 i 组的变异，有 2 1 2 1 2 1 1 2 1 2 1 2 ( ) ( ) ( ) 2( )( ) ( ) ( ) ( ) y y n y y y y y y y y y y y y y y y y i n j i j i n j i n j i j i i n j i j i n j i j i i n j i j = − + − = − + − − + − − = − + −       = = = = = =

从而总变异(61)可以剖分为： sS,0-=0,+2-列 (63) 即 总平方和=组内（误差）平方和+处理平方和 组间变异由k个的变异引起，故其自由度=k一1，组 间平方和SS为： s8,=吃-2=r2n-C (64) 组内变异为各组内观察值与组平均数的变异，故每组具有 自由度v=n一1和平方和2(y,-,)2；而资料共有k组，故组 内自由度v=k(n一1)，组内平方和SS。为： SS。=2[(y,-,)2]=SSr-SS, (65)

从而总变异(6·1)可以剖分为: =   − =   − +  − = = = = = k i i k i n j i j i k i n j T i j SS y y y y n y y 1 2 1 1 2 1 1 2 ( ) ( ) ( ) （6·3） 即 总平方和=组内(误差)平方和+处理平方和 组间变异由k个 的变异引起，故其自由度 v =k－1 , 组 间平方和 SSt 为： i y =  − =  − k k SSt n yi y Ti n C 1 1 2 2 ( ) 组内变异为各组内观察值与组平均数的变异，故每组具有 自由度 v =n－1和平方和 ；而资料共有k 组，故组 内自由度 v = k (n－1) ,组内平方和 SSe 为：  − n ij i y y 1 2 ( ) =   − = − k n e i j i SST SSt SS y y 1 1 2 [ ( ) ] (6·5) （6·4）

因此，得到表6.1类型资料的自由度分解式为： (nk-1)=(k-1)+k(n-1) (66) 总自由度DFT=组间自由度DF+组内自由度DFe 求得各变异来源的自由度和平方和后，进而可得： 总的均方 s,=s=∑∑y9 nk-1 组间的均方 s,=52=1 2- (67) k-2 组内均方 8==2g- k(n-1)

因此，得到表6.1类型资料的自由度分解式为： (nk −1)=(k −1)+ k(n −1) (6·6) 总自由度DFT =组间自由度DFt +组内自由度DFe 求得各变异来源的自由度和平方和后，进而可得: (6·7)            − − = = − − = = − − = =    ( ) ( ) ( ) ( ) 1 2 1 2 2 2 2 2 2 k n y y MS s k n y y MS s nk y y MS s i j i e e i t t i j T T 组内均方 组间的均方 总的均方

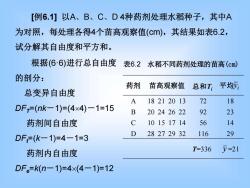
[例6.1]以A、B、C、D4种药剂处理水稻种子，其中A 为对照，每处理各得4个苗高观察值(c),其结果如表6.2， 试分解其自由度和平方和。 根据(66)进行总自由度 表6.2 水稻不同药剂处理的苗高(cm) 的剖分： 药剂 苗高观察值总和T: 平均， 总变异自由度 A 18212013 72 18 DF=(nk-1)=(4×4)-1=15 B 20242622 92 23 药剂间自由度 C 10151714 56 14 DF=(k-1)=4-1=3 D 28272932 116 29 药剂内自由度 T=336 y=21 DFe=k(n-1)=4×(4-1)=12

[例6.1] 以A、B、C、D 4种药剂处理水稻种子，其中A 为对照，每处理各得4个苗高观察值(cm)，其结果如表6.2， 试分解其自由度和平方和。 表6.2 水稻不同药剂处理的苗高(cm) 药剂 苗高观察值 总和Ti 平均 A 18 21 20 13 72 18 B 20 24 26 22 92 23 C 10 15 17 14 56 14 D 28 27 29 32 116 29 T=336 =21 i y y 根据(6·6)进行总自由度 的剖分： 总变异自由度 DFT=(nk－1)=(44)－1=15 药剂间自由度 DFt=(k－1)=4－1=3 药剂内自由度 DFe =k(n－1)=4(4－1)=12

根据(63)进行总平方和的剖分： C-T2-336 =7056 nk4×4 SS=∑∑号-C=182+212++322-C=602 s,=n20-2=∑T2/n-C =(722+922+562+1162)/4-C=504 或 SS,=4×[18-21)2+(23-21)2+(14-21)2+(29-21)2]=504 -220,-6-立4 =SS7-SS=602-504=98

根据(6·3)进行总平方和的剖分： 7056 4 4 336 2 2 =  = = nk T C 18 21 32 602 2 2 2 2 SST =yi j −C = + ++ −C = (72 92 56 116 ) 4 504 ( ) 2 2 2 2 1 2 2 = + + + − = =  − =  − / C SS n y y T n C k t i i 或 4 [(18 21) (23 21) (14 21) (29 21) ] 504 2 2 2 2 SSt =  − + − + − + − = 602 504 98 ( ) 1 1 1 1 2 2 2 = − = − = =  − =  − T t k n n k k e i j i i j i SS SS SS y y y T n

或 药剂A内：SS。=182+212+202+132-72/4=38 药剂B内：SS。,=202+242+262+222-92/4=20 药剂C内：SS。,=102+152+17+142-562/4=26 药剂D内：SS。=282+27+292+322-1162/4=14 所以 59.=22,-P=38+20+26+14=98 进而可得均方： MS,=s7=602/15=40.13 MS,=s2=504/3=168.00 MS。=s=98/12=8.17

或 药剂A内： 药剂B内： 药剂C内： 药剂D内： 18 21 20 13 72 4 38 2 2 2 2 2 1 SSe = + + + − = 20 24 26 22 92 4 20 2 2 2 2 2 2 SSe = + + + − = 10 15 17 14 56 4 26 2 2 2 2 2 3 SSe = + + + − = 28 27 29 32 116 4 14 2 2 2 2 2 4 SSe = + + + − = 所以 =  − = + + + = k n e i j i SS y y 1 1 2 ( ) 38 20 26 14 98 进而可得均方： 602 15 4013 2 MS s / . T = T = = 504 3 168 00 2 MS s / . t = t = = 98 12 817 2 MS s / . e = e = =

二、F分布与F测验 在一个平均数为4、方差为。2的正态总体中，随机抽 取两个独立样本，分别求得其均方S12和S22,将S2和S22 的比值定义为F: F)=s/s好 (68) 此F值具有s2的自由度，和S22的自由度2。 所谓F吩布，就是在给定的y,和2下按上述方法从正 态总体中进行一系列抽样，就可得到一系列的F值而作成 一个分布。 米F分布下一定区间的概率可从已制成的统计表查出

二、F分布与F测验 在一个平均数为 、方差为 的正态总体中，随机抽 取两个独立样本，分别求得其均方 s1 2 和 s2 2，将 s1 2 和 s2 2 的比值定义为F：  2  2 2 2 ( ) 1 F = s s  1 ， 2 （6·8） 此F值具有s1 2 的自由度 v1 和 s2 2 的自由度 v2。 所谓F分布，就是在给定的 v1 和 v2 下按上述方法从正 态总体中进行一系列抽样，就可得到一系列的F 值而作成 一个分布。 F分布下一定区间的概率可从已制成的统计表查出