上海交通大学：《现代控制理论 Modern Control Theory》课程教学资源（课件讲稿）第二章 状态空间描述

上誉文廷大￥ SHANGHAI JIAO TONG UNIVERSITY 第二章状态空间描述 2.1基本概念 典型控制系统方框图 被控对象 状态x 控制4 输出业 执行器 被控过程 传感器 反馈控制 控制器 输入r (1)系统：一些相互制约的部分所构成的整体 典型的控制系统由被控对象、传感器、执行器和控制器组成 (2)输入和输出： 输入---由外部施加到系统上的全部激励 输出-一一 从外部量测到的来自系统的信息

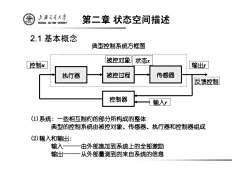
第二章 状态空间描述 2.1 基本概念 典型控制系统方框图 执行器 被控过程 传感器 控制器 输入 r 控制 u 输出y 被控对象 状态x 反馈控制 (1)系统：一些相互制约的部分所构成的整体 典型的控制系统由被控对象、传感器、执行器和控制器组成 (2)输入和输出： 输入------由外部施加到系统上的全部激励 输出------从外部量测到的来自系统的信息

上游文通大￥ SHANGHAI JIAO TONG UNIVERSITY 嘉兴民丰造纸厂 造纸生产过程控制流程图 浆阀 水 中浓纸浆42 一 蒸汽阀 V-43 混合箱 哈1蒸汽阀 V40 流浆箱 网 88 压榨 88 烘缸 表面施胶 网前部 网部、压榨部 第一干燥部 第二干燥部

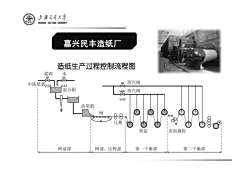
造纸生产过程控制流程图 嘉兴民丰造纸厂

上游文通大￥ SHANGHAI JIAO TONG UNIVERSITY (3)线性系统：对任何输入4，和42，系统H(u)满足叠加原理 叠加原理：H(+w2)=H(u)+H(2) (4)状态：表征系统在时间域中运动的信息和行为，如x(t,) (⑤)状态变量：能够完全表征系统运动状态的最小个数的一组变量 例如：由x(to)和u(t)确定系统在任意时刻t的状态 (6)状态向量：以系统的个状态变量作为分量的向量 x()=[x(t),…,xn(t)] (T)状态空间：以状态变量x(t),…,x,(t)为坐标轴构成的维空间

(4)状态：表征系统在时间域中运动的信息和行为，如 (6)状态向量：以系统的 n个状态变量作为分量的向量 [ ] T 1 () , , () () n xt x x = t t L (5)状态变量：能够完全表征系统运动状态的最小个数的一组变量 例如: 由 和 x t( ) 0 u(t)确定 了系统在任意时刻t的状态 (3)线性系统：对任何输入 和 ，系统 满足叠加原理 叠加原理： ( ) ( ) ( ) H u1 + u 2 = H u1 + H u 2 H(u) 1 u 2 u (7)状态空间：以状态变量 为坐标轴构成的 ,, x x 1() () t t L n n维空间 0 x t( )

上誉文廷大￥ SHANGHAI JIAO TONG UNIVERSITY (8)状态方程：描述系统状态与输入之间关系的、一阶微分方程： x=Ax+Bu (9)输出方程：描述系统输出与状态、输入之间关系的数学表达式： y=Cx+Du (10)状态空间模型：状态方程+输出方程 回旧回 =Ax+Bu y=Cx+Du 其中为状态矩阵，B为输入矩阵，C为输出矩阵，D为直接传递矩阵

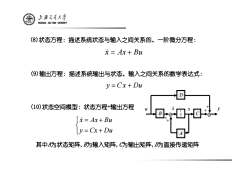
(10)状态空间模型：状态方程+输出方程 其中 A为状态矩阵, B为输入矩阵, C为输出矩阵, D为直接传递矩阵 ⎩ ⎨ ⎧ = + = + y Cx Du x& Ax Bu (8)状态方程：描述系统状态与输入之间关系的、一阶微分方程： x& = Ax + Bu (9)输出方程：描述系统输出与状态、输入之间关系的数学表达式： y = C x + Du B S I C D A u x& x y + + + +

上游文通大￥ SHANGHAI JIAO TONG UNIVERSITY 设单输入-单输出线性系统的状态变量为：x(t),x2(t)…,xn(t) 状态方程的一般形式为： 元1=a11x1+a12X2+…+a1mXn+bu X2 =a2+a22x2+..+a2nxn+bzu 年●n0 xn amx+an2x2 +.amxn +bnu 输出方程的一般形式为： y=CX+Cx+Cx

设单输入-单输出线性系统的状态变量为： 状态方程的一般形式为: ( ), ( ) , ( ) 1 2 x t x t x t L n x a x a x a x b u x a x a x a x b u x a x a x a x b u n n n nn n n n n n n = + + + + = + + + + = + + + + & L L L & L & L 1 1 2 2 2 21 1 22 2 2 2 1 11 1 12 2 1 1 输出方程的一般形式为: n n y = c x + c x + L + c x 1 1 2 2

上游文通大￥ SHANGHAI JIAO TONG UNIVERSITY 写成一阶矩阵微分方程的形式为 元1 a12 b 元2 021 022 02n X2 b2 三 An2 xn」 可简写为： n×n方阵 n×1列阵 y=c a X2 Cn .: du =Ax+bu y=cx+du 1x1变量 >状态变量的选择不是唯一的 1xn行阵 1x1常数 >状态变量可以是虚构的量，无 物理意义 nx1变量

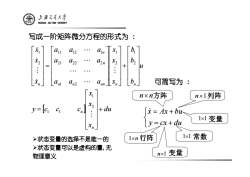
写成一阶矩阵微分方程的形式为 : [ ] du x x x y c c c u b b b x x x a a a a a a a a a x x x n n n n nn n n n n n + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ M M L L L L L & M & & 2 1 1 1 2 1 2 1 1 2 21 22 2 11 12 1 2 1 变量 n × n方阵 1 × n 行阵 n × 1列阵 1 × 1 常数 ⎩ ⎨ ⎧ = + = + y cx du x& Ax bu 1 × 1 变量 n × 1 可简写为 : ¾状态变量的选择不是唯一的 ¾状态变量可以是虚构的量,无 物理意义

上商文通大￥ SHANGHAI JIAO TONG UNIVERSITY 具有个输入和个输出的系统的状态方程一般形式为： x1=a11+a2x2+…+anxn+b24+b242+…+b,4, x2=a21x1+a22X2+…+a2nmXn+b2141+b2242+…+b2,u 元n=anX1+an2x2+…+AmXn+bni24+bn242+…+bnm4, 输出方程的一般形式为： y=Cx+C12x2+…+Cmxn+d1h1+d12W2+…+d,u, y2=C211+C22X2+…+C2mXn+d2i41+d2u2+…+d2,, ym Cm+Cm2X2++Cmnx +dmu +dm2u2++dmur

具有r个输入和m个输出的系统的状态方程一般形式为: n n n nn n n n nr r n n r r n n r r x a x a x a x b u b u b u x a x a x a x b u b u b u x a x a x a x b u b u b u = + + + + + + + = + + + + + + + = + + + + + + + & L L LL & L L & L L 1 1 2 2 1 1 2 2 2 21 1 22 2 2 21 1 22 2 2 1 11 1 12 2 1 11 1 12 2 1 m m m mn n m m mr r n n r r n n r r y c x c x c x d u d u d u y c x c x c x d u d u d u y c x c x c x d u d u d u = + + + + + + + = + + + + + + + = + + + + + + + L L LL L L L L 1 1 2 2 1 1 2 2 2 21 1 22 2 2 21 1 22 2 2 1 11 1 12 2 1 11 1 12 2 1 输出方程的一般形式为：

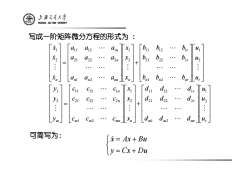
上文大学 SHANGHAI JIAO TONG UNIVERSITY 写成一阶矩阵微分方程的形式为 无 a12 n 元2 01 02 02n X2 b21 b22 bzr Uz . .: an an2 bn 为 C11 C12 X d u 2 C21 C22 C2n x2 d2 d uz 三 . + .: ym Cml Cm2 Cmn dm … u, 可简写为： =Ax+Bu y=Cx+Du

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ m m mr r r r m m mn n n n m n n nr r r r n n nn n n n n u u u d d d d d d d d d x x x c c c c c c c c c y y y u u u b b b b b b b b b x x x a a a a a a a a a x x x M L L L L L M L L L L L M M L L L L L M L L L L L & M & & 2 1 1 2 21 22 2 11 12 1 2 1 1 2 21 22 2 11 12 1 2 1 2 1 1 2 21 22 2 11 12 1 2 1 1 2 21 22 2 11 12 1 2 1 可简写为： 写成一阶矩阵微分方程的形式为 : ⎩ ⎨ ⎧ = + = + y Cx Du x& Ax Bu

上游文通大￥ SHANGHAI JIAO TONG UNIVERSITY 口建立状态空间模型的步骤： 1)选择合适的状态变量 2)根据系统物理机理或其他方面的机理列写微分方程， 化成一阶微分方程组 3)写成矩阵形式，得到状态空间模型 ▣建立状态空间模型的常用方法： 1)采用机理分析法建模 2)根据系统传递函数建模

‡ 建立状态空间模型的步骤: 1) 选择合适的状态变量 2) 根据系统物理机理或其他方面的机理列写微分方程, 化成一阶微分方程组 3) 写成矩阵形式, 得到状态空间模型 ‡ 建立状态空间模型的常用方法: 1) 采用机理分析法建模 2) 根据系统传递函数建模

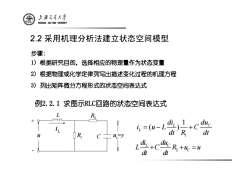
上游文通大￥ SHANGHAI JIAO TONG UNIVERSITY 2.2采用机理分析法建立状态空间模型 步骤： 1)根据研究目的，选择相应的物理量作为状态变量 2)根据物理或化学定律列写出描述变化过程的机理方程 3)列出矩阵微分方程形式的状态空间表达式 例2.2.1求图示RLC回路的状态空间表达式 L R i.=(u- d)1+ duc dt u R uy R diL+C dt duc R+uc=u dt

2.2 采用机理分析法建立状态空间模型 步骤: 1) 根据研究目的，选择相应的物理量作为状态变量 2) 根据物理或化学定律列写出描述变化过程的机理方程 3) 列出矩阵微分方程形式的状态空间表达式 1 1 ( ) L C L di du i uL C dt R dt =− + 2 L C C di du L C Ru u dt dt + + = 例2.2.1 求图示RLC回路的状态空间表达式 u L c u R2 R1 Li + - C =y