《控制理论》课程教学资源（参考书籍）定量过程控制理论 Quantitative Process Control Theory_Chapter 09 Complex Control Strategies

Chapter 9 Complex Control Strategies 4口，+@，4定4=定0C Zhang.W.D..CRC Press.2011 Version 1.0 1/95

Chapter 9 Complex Control Strategies Zhang, W.D., CRC Press, 2011 Version 1.0 1/95

Complex Control Strategies 19.1 The 2DOF Structure for Stable Plants 29.2 2DOF Structure for Unstable Plants 3 9.3 Cascade Control 49.4 Anti-Windup Structure 59.5 Feedforward Control 69.6 Optimal Input Disturbance Rejection 79.7 Control of Plants with Multiple Time Delays 4口，+@4定4生，定分0C0 Zhang.W.D..CRC Press.2011 Version 1.0 2/95

Complex Control Strategies 1 9.1 The 2DOF Structure for Stable Plants 2 9.2 2DOF Structure for Unstable Plants 3 9.3 Cascade Control 4 9.4 Anti-Windup Structure 5 9.5 Feedforward Control 6 9.6 Optimal Input Disturbance Rejection 7 9.7 Control of Plants with Multiple Time Delays Zhang, W.D., CRC Press, 2011 Version 1.0 2/95

Section 9.1 The 2DOF Structure for Stable Plants 9.1 The 2DOF Structure for Stable Plants 1DOF System The effect of the reference on the error was the same as that of the output disturbance on the system output: e(s)y(s) 1 r(s)-d(s)-1+G(s)C(s) Such a system has merely one degree of freedom.When the reference and the disturbance have similar dynamic characteristics (for example,both of them are steps),a 1DOF controller can simultaneously satisfy the requirement on tracking response and disturbance response in many cases 4口，+@，4定4定90C Zhang.W.D..CRC Press.2011 Version 1.0 3/95

Section 9.1 The 2DOF Structure for Stable Plants 9.1 The 2DOF Structure for Stable Plants 1DOF System The effect of the reference on the error was the same as that of the output disturbance on the system output: e(s) r(s) = y(s) d(s) = 1 1 + G(s)C(s) Such a system has merely one degree of freedom. When the reference and the disturbance have similar dynamic characteristics (for example, both of them are steps),a 1DOF controller can simultaneously satisfy the requirement on tracking response and disturbance response in many cases Zhang, W.D., CRC Press, 2011 Version 1.0 3/95

Section 9.1 The 2DOF Structure for Stable Plants Why do we Need a 2DOF System Sometimes,the dynamic characteristics of the reference and the disturbance are different.For example,the reference is a step while the disturbance at the plant output is a ramp If both good tracking response and good disturbance response are desired,the controller that achieves the two goals may not exist. In this case,an additional controller may have to be introduced so that the tracking response and the disturbance response can be adjusted independently.There are two loops in this system: o One is the reference loop,which is from the reference to the system output o The other is the disturbance loop,which is from the disturbance at the plant output to the system output Such a system is of 2DOF Zhang.W.D..CRC Press.2011 Version 1.0 4/95

Section 9.1 The 2DOF Structure for Stable Plants Why do we Need a 2DOF System Sometimes, the dynamic characteristics of the reference and the disturbance are different. For example, the reference is a step while the disturbance at the plant output is a ramp If both good tracking response and good disturbance response are desired, the controller that achieves the two goals may not exist. In this case, an additional controller may have to be introduced so that the tracking response and the disturbance response can be adjusted independently. There are two loops in this system: One is the reference loop, which is from the reference to the system output The other is the disturbance loop, which is from the disturbance at the plant output to the system output Such a system is of 2DOF Zhang, W.D., CRC Press, 2011 Version 1.0 4/95

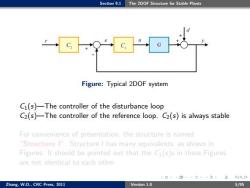
Section 9.1 The 2DOF Structure for Stable Plants Figure:Typical 2DOF system C1(s)-The controller of the disturbance loop C2(s)-The controller of the reference loop.C2(s)is always stable For convenience of presentation,the structure is named "Structure I".Structure I has many equivalents,as shown in Figures.It should be pointed out that the C(s)s in these Figures are not identical to each other 4口，404注4生定分QC Zhang.W.D..CRC Press.2011 Version 1.0 5/95

Section 9.1 The 2DOF Structure for Stable Plants Figure: Typical 2DOF system C1(s)—The controller of the disturbance loop C2(s)—The controller of the reference loop. C2(s) is always stable For convenience of presentation, the structure is named “Structure I”. Structure I has many equivalents, as shown in Figures. It should be pointed out that the C1(s)s in these Figures are not identical to each other Zhang, W.D., CRC Press, 2011 Version 1.0 5/95

Section 9.1 The 2DOF Structure for Stable Plants Figure:Typical 2DOF system C1(s)-The controller of the disturbance loop C2(s)-The controller of the reference loop.C2(s)is always stable For convenience of presentation,the structure is named "Structure I".Structure I has many equivalents,as shown in Figures.It should be pointed out that the Ci(s)s in these Figures are not identical to each other 4口，+@4定4定， 定9aC Zhang.W.D..CRC Press.2011 Version 1.0 5/95

Section 9.1 The 2DOF Structure for Stable Plants Figure: Typical 2DOF system C1(s)—The controller of the disturbance loop C2(s)—The controller of the reference loop. C2(s) is always stable For convenience of presentation, the structure is named “Structure I”. Structure I has many equivalents, as shown in Figures. It should be pointed out that the C1(s)s in these Figures are not identical to each other Zhang, W.D., CRC Press, 2011 Version 1.0 5/95

Section 9.1 The 2DOF Structure for Stable Plants C Figure:An equivalent of the typical 2DOF system 1 G Figure:Another equivalent of the typical 2DOF system 4口，4日，4注4生，定9QC Zhang,W.D..CRC Press.2011 Version 1.0 6/95

Section 9.1 The 2DOF Structure for Stable Plants Figure: An equivalent of the typical 2DOF system Figure: Another equivalent of the typical 2DOF system Zhang, W.D., CRC Press, 2011 Version 1.0 6/95

Section 9.1 The 2DOF Structure for Stable Plants Internal stability:Consider the typical 2DOF system.The input-output relationship is as follows: e(s) C2(s) r(s) 1+G(s)C1(S) y(s) 1 d(s) 1+G(s)C1(s) It can be seen that the internal stability of the closed-loop system is only determined by Ci(s).The analysis for the internal stability is similar to that in a 1DOF system Design:The design of a 2DOF system involves two steps: Design C1(s)for good disturbance response @Design C2(s)for good tracking response 4口，+@，4定4=定0C Zhang.W.D..CRC Press.2011 Version 1.0 7/95

Section 9.1 The 2DOF Structure for Stable Plants Internal stability: Consider the typical 2DOF system. The input-output relationship is as follows: e(s) r(s) = C2(s) 1 + G(s)C1(s) y(s) d(s) = 1 1 + G(s)C1(s) It can be seen that the internal stability of the closed-loop system is only determined by C1(s). The analysis for the internal stability is similar to that in a 1DOF system Design: The design of a 2DOF system involves two steps: 1 Design C1(s) for good disturbance response 2 Design C2(s) for good tracking response Zhang, W.D., CRC Press, 2011 Version 1.0 7/95

Section 9.1 The 2DOF Structure for Stable Plants Internal stability:Consider the typical 2DOF system.The input-output relationship is as follows: e(s) C2(s) r(s) 1+G(s)C1(S) y(s) 1 d(s) 1+G(s)C1(s) It can be seen that the internal stability of the closed-loop system is only determined by Ci(s).The analysis for the internal stability is similar to that in a 1DOF system Design:The design of a 2DOF system involves two steps: DDesign C1(s)for good disturbance response 2Design C2(s)for good tracking response 4口：4@4242定90C Zhang,W.D..CRC Press.2011 Version 1.0 7/95

Section 9.1 The 2DOF Structure for Stable Plants Internal stability: Consider the typical 2DOF system. The input-output relationship is as follows: e(s) r(s) = C2(s) 1 + G(s)C1(s) y(s) d(s) = 1 1 + G(s)C1(s) It can be seen that the internal stability of the closed-loop system is only determined by C1(s). The analysis for the internal stability is similar to that in a 1DOF system Design: The design of a 2DOF system involves two steps: 1 Design C1(s) for good disturbance response 2 Design C2(s) for good tracking response Zhang, W.D., CRC Press, 2011 Version 1.0 7/95

Section 9.1 The 2DOF Structure for Stable Plants C1(s):The design of Cl(s)is the same as that for the controller in a 1DOF system C2(s):After C1(s)is designed,the loop consisting of C1(s)and G(s)is viewed as an augmented plant,of which the transfer function is denoted by T(s).The system that consists of C2(s) and T(s)forms the IMC structure with an exact model. Accordingly,C2(s)can be directly designed To illustrate the design procedure,consider the following plant: G(s= T5+1 The system is required to track a step reference,and at the same time to reject the disturbance that is in the form of a ramp at the plant output 4口，+@，4定4定90C Zhang.W.D..CRC Press.2011 Version 1.0 8/95

Section 9.1 The 2DOF Structure for Stable Plants C1(s): The design of C1(s) is the same as that for the controller in a 1DOF system C2(s): After C1(s) is designed, the loop consisting of C1(s) and G(s) is viewed as an augmented plant, of which the transfer function is denoted by T(s). The system that consists of C2(s) and T(s) forms the IMC structure with an exact model. Accordingly, C2(s) can be directly designed To illustrate the design procedure, consider the following plant: G(s) = K τ s + 1 e −θs The system is required to track a step reference, and at the same time to reject the disturbance that is in the form of a ramp at the plant output Zhang, W.D., CRC Press, 2011 Version 1.0 8/95