上海交通大学：《现代控制理论基础》课程教学资源（课件讲稿）第六章 状态反馈和状态观测器

第六章 状态反馈和状态观测器

第六章 状态反馈和状态观测器

6.1引言 (1)研究自动控制系统有三大命题：模型、分析和综合。 前面几章讨论的是线性系统数学模型的建立，以及系统的分 析问题。 系统的分析是已知系统的结构参数，在外界输入或扰动作 用下，定量或定性分析系统的性能（系统的响应、 稳定性、 和能控行、能观性)问题 系统的综合也称系统的设计问题，与系统分析相反，它是 在给定系统基本结构、参数的前提下，设计一种控制器，它 产生的控制作用能使系统达到期望的性能。 系统的控制有两种：开环控制和闭环控制（反馈控制）。 反馈控制对于系统抗干扰和抗参数变动等方面均有较强的作 用，被广泛应用。反馈有两种形式：状态反馈与输出反馈

6.1 引 言 ⑴ 研究自动控制系统有三大命题：模型、分析和综合。 系统的综合也称系统的设计问题，与系统分析相反，它是 在给定系统基本结构、参数的前提下，设计一种控制器，它 产生的控制作用能使系统达到期望的性能。 前面几章讨论的是线性系统数学模型的建立，以及系统的分 析问题。 系统的分析是已知系统的结构参数，在外界输入或扰动作 用下，定量或定性分析系统的性能（系统的响应、稳定性、 和能控行、能观性）问题 系统的控制有两种：开环控制和闭环控制（反馈控制）。 反馈控制对于系统抗干扰和抗参数变动等方面均有较强的作 用，被广泛应用。 反馈有两种形式：状态反馈与输出反馈

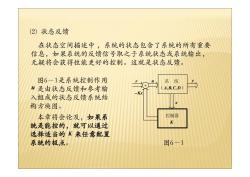
2)状态反馈 在状态空间描述中，系统的状态包含了系统的所有重要 信息，如果系统的反馈信号取之于系统状态或系统输出， 无疑将会获得性能更好的控制。这就是状态反馈。 图6-1是系统控制作用 系统 M是由状态反馈和参考输 A,B,C,D -Kx 入组成的状态反馈系统结 构方块图。 本章将会论及，如果系 控制器 统是能控的，就可以通过 K 选择适当的K来任意配置 系统的极，点。 图6-1

在状态空间描述中 ，系统的状态包含了系统的所有重要 信息，如果系统的反馈信号取之于系统状态或系统输出， 无疑将会获得性能更好的控制。这就是状态反馈。 （ ） 系 统 A,B,C, D K 控制器 x r + −Kx u y 图6－1 图6－1是系统控制作用 是由状态反馈和参考输 入组成的状态反馈系统结 构方块图。 本章将会论及，如果系 统是能控的，就可以通过 选择适当的 来任意配置 系统的极点 。 K u ⑵ 状态反馈

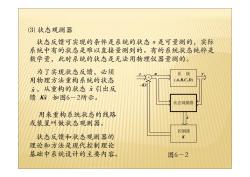
3)状态观测器 状态反馈可实现的条件是系统的状态x是可量测的，实际 系统中有的状态是难以直接量测到的。有的系统状态纯粹是 数学量，此时系统的状态是无法用物理仪器量测的。 为了实现状态反馈，必须 系统 用物理方法重构系统的状态 (A,B,C,D) ,从重构的状态引出反 馈配如图6-2所示。 状态观测器 用来重构系统状态的线路 或装置叫做状态观测器。 控制器 状态反馈和状态观测器的 K 理论和方法是现代控制理论 基础中系统设计的主要内容。 图6-2

⑶ 状态观测器 状态反馈可实现的条件是系统的状态 是可量测的，实际 系统中有的状态是难以直接量测到的。有的系统状态纯粹是 数学量，此时系统的状态是无法用物理仪器量测的。 x 状态观测器 K 控制器 x ˆ r + −Kxˆ u (A,B,C,D) 系 统 y 图6－2 为了实现状态反馈，必须 用物理方法重构系统的状态 ，从重构的状态 引出反 馈 如图6－2所示。 x ˆ x ˆ Kxˆ 用来重构系统状态的线路 或装置叫做状态观测器。 状态反馈和状态观测器的 理论和方法是现代控制理论 基础中系统设计的主要内容

(4)本章主要内容 ①状态反馈：线性定常系统状态反馈对系统的影响，状态反 馈可任意配置系统极，点的条件和计算方法。 ② 状态观测器：状态观测器能重构状态的条件和设计方法。 用求解西尔维斯特(Sylvester)方程的方法设计 状态反馈和状态观测器。 ③状态反馈的应用：系统的镇定、系统解耦和无静差跟踪系 统的综合问题 ④线性二次型最优控制的理论及设计控制器的方法

① 状态反馈：线性定常系统状态反馈对系统的影响， 状态反 馈可任意配置系统极点的条件和计算方法 。 ⑷ 本章主要内容 ② 状态观测器：状态观测器能重构状态的条件和设计方法。 用求解西尔维斯特（ ）方程的方法设计 状态反馈和状态观测器 。 ③ 状态反馈的应用：系统的镇定 、系统解耦和无静差跟踪系 统的综合问题 ④ 线性二次型最优控制的理论及设计控制器的方法 Sylvester

62反馈系统的状态空间描述 6.2.1状态反馈系统的状态空间描述 状态反馈系统的结构图如图6一3所示。 -Kx 图6一3状态反馈系统的结构图

6.2 反馈系统的状态空间描述 A － K B ∫ r u y C x －Kx + + 图6－3 状态反馈系统的结构图 6.2.1 状态反馈系统的状态空间描述 状态反馈系统的结构图如图6－3所示

设原系统的状态空间描述为 ∑： =Ax+Bu (6-1) y=Cx+Du 引入状态反馈，闭环系统的控制规律（输入）为 u=r-Kx (6—2) 式中，r是系统的参考输入，K是p×n状态反馈阵。 闭环系统状态空间描述：将(6一2)代入式(6一1)得 =Ax+B(r-Kx)=(A-BK)x+Br y=Cx+D(r-Kx)=(C-DK)x+Dr 若D=0,则 : 文=(A-BK)x+Br y=Cx

设原系统的状态空间描述为 y Cx Du Σ : x Ax Bu = + & = + 引入状态反馈 ，闭环系统的控制规律(输入)为 Kx u = r －Kx 式中， 是系统的参考输入， 是 状态反馈阵。 r K p × n ( 6－1) ( 6—2) y Cx D r Kx C DK x Dr x Ax B r Kx A BK x Br = + = + = + = + ( ) ( ) ( ) ( ) － － & － － 若 ，则 D = 0 y Cx Σ : x A BK x Br = f & = ( － ) + ( 6—4) ( 6—3) 闭环系统状态空间描述：将( 6－2)代入式( 6－1)得

带状态反馈的闭环系统的传递函数阵为 G(s)=C(sI-(A-BK))-B (6—5) G(s)是q×p阵。 原系统的性能主要由A的特征值（系统的极，点)决定，状态 反馈系统的极，点是A一BK的特征值，有可能通过的选择K来任 意配置系统的极，点

带状态反馈的闭环系统的传递函数阵为 G C I A BK B1 ( ) ( ( )) − f s = s − － ( 6—5) (s) G f 是 阵。 q × p 原系统的性能主要由 的特征值（系统的极点）决定，状态 反馈系统的极点是 的特征值，有可能通过的选择 来任 意配置系统的极点。 A －BK K A

6.2.2 输出反馈系统的状态空间描述 图6一4输出反馈系统的结构图 输出反馈系统的控制规律是 (6-6) 式中，F是pxg输出反馈阵。代入式(6一1)得 =(A-BFC)x+Br y=(C-DFC)x+Dr (6-7)

6.2.2 输出反馈系统的状态空间描述 图6－4输出反馈系统的结构图 输出反馈系统的控制规律是 式中， 是 输出反馈阵。代入式 F p × q ( 6—1) 得 （6－6） + + A B C − F − Fx ∫ r u y x y C DFC x Dr x A BFC x Br = + = + ( ) ( ) － & － （6－7）

若D=0,则有 Ed: =(A-BFC)x+Br (6-8) y=Cx 带输出反馈的闭环系统的传递函数阵为 Gor(s)=C(sI-(A-BFC))-B (6-9) Gg(s)是9×p阵。 原系统的传递函数阵为 G(s)=C(sI-A)B (6-10) 则 G(s)=G(s)(I+FG(s) (6-11) 或 Gr(s)=(I+FG(s))G(s) (6-12) 输出反馈也可以通过F来改变系统的极，点，但它不能像状态 反馈那样任意配置系统的极，点。因为通常方程℉C=K的解不 存在

若 ，则有 D = 0 y Cx Σ : x A BFC x Br = cf & = ( － ) + 带输出反馈的闭环系统的传递函数阵为 G C I A BFC B1 ( ) ( ( ))− cf s = s − － Gcf (s)是 阵。 q× p G C I A B1 ( ) ( ) − s = s − 1 ( ) ( )( ( )) − s = s + s Gcf G I FG 则 ( ) ( ( )) ( ) 1 s s s Gcf I FG G− = + 或 输出反馈也可以通过 来改变系统的极点，但它不能像状态 反馈那样任意配置系统的极点。因为通常方程 的解不 存在。 F FC = K 原系统的传递函数阵为 （6－8） （6－9） （6－10） （6－11） （6－12）