西安电子科技大学：《概率论与数理统计》课程教学课件（讲稿）第三章 多维随机变量及其分布 3.2 边缘分布 3.3 条件分布

第三章多维随机变量及其分布 9§3.1二维随变量 9§3.2边缘分布 9§3.3条件分布 9§3.4相互独立的随机变量 。§3.5两个随机变量的函数的分布

第三章 多维随机变量及其分布  §3.1 二维随机变量  §3.2 边缘分布  §3.3 条件分布  §3.4 相互独立的随机变量  §3.5 两个随机变量的函数的分布

第三章多维随机变量及其分布 9§3.1二维随机变量 9§3.2边缘分布 9§3.3条件分布 。§3.4相互独立的随机变量 9§3.5两个随机变量的函数的分布

第三章 多维随机变量及其分布  §3.1 二维随机变量  §3.2 边缘分布  §3.3 条件分布  §3.4 相互独立的随机变量  §3.5 两个随机变量的函数的分布

§3.2边缘分布 例4设二维随机变量(X,Y)的概率密度为 1 f(x,y)= 2m102V1-p exp 2(-p) -00,02>0， -1<p<1. 试求二维正态随机变的边缘概率密度

设二维随机变量(X,Y)的概率密度为                        2 2 2 2 1 2 1 2 2 1 2 1 2 2 1 2 ( )( ) ( ) 2 ( ) 2(1 ) 1 exp 2 1 1 ( , ) σ y μ σ σ x μ y μ ρ σ x μ ρ σ σ ρ f x y  试求二维正态随机变量的边缘概率密度.    x  ,    y  , 1 1. , , , , , 0, 0, 1 2 1 2 1 2      ρ 其 中 μ μ σ σ ρ 都是常数 且 σ σ 例4 §3.2 边缘分布

§3.2边缘分布 -1=4-2p=40=2+y- 002 解fx(x)=f(x,)d, 由于 "-[- 2 02 于是 1 fx(x)= 令=-2}

解 f (x) f (x, y)d y, X     由于 1 2 1 2 2 2 2 2 ( )( ) 2 ( ) σ σ x μ y μ ρ σ y μ     , ( ) 2 1 2 2 1 2 1 1 2 2 σ x μ ρ σ x μ ρ σ y μ             于是 , 2π 1 ( ) 2 1 1 2 2 2 2 1 2 1 2(1 ) 1 2 ( ) 2 1 1 2 e e dy σ σ ρ f x σ x μ ρ σ y μ σ ρ x μ X                   , 1 1 1 1 2 2 2            σ x μ ρ σ y μ ρ 令 t §3.2 边缘分布 2 2 1 1 2 2 2 2 2 2 1 1 2 2 1 2 1 1 ( ) ( )( ) ( ) ( , ) exp 2 2 1 2(1 ) x μ x μ y μ y μ f x y ρ σ σ ρ ρ σ σ σ σ                           

§3.2边缘分布 由于-oy<o所以-0<K0,而d=Vi-p -(x-41)2 产3 、 则有fx(x) 22o7 01 1 -x-41)2 即 fx(x)= e 21 一0<X<00. V2π01 同理可得 (y-2)2 fy(y)= -e ， -0<y<0. √2π02 二维正态分布的两个边缘分布都是一维正态分 布，并且都不依赖与参数p 联合分布包含更多的信息，由联合分布可以求出边 缘分布，但由边缘分布一般无法求出联合分布

则有 d , 2 1 ( ) 2 2 ( ) 1 2 2 1 2 1 e e t σ f x t σ x μ X         , . 2π 1 ( ) 2 1 2 1 2 ( ) 1         e x σ f x σ x μ 即 X 同理可得 二维正态分布的两个边缘分布都是一维正态分 布，并且都不依赖与参数r , . 2 1 ( ) 2 2 2 2 2 ( ) 2         e y σ f y σ y μ Y  §3.2 边缘分布 联合分布包含更多的信息,由联合分布可以求出边 缘分布,但由边缘分布一般无法求出联合分布 由于－∞<y<∞所以－∞<t<∞，而dt＝dy 2 2 1 1   r

§3.2边缘分布 边缘分布均为正态分布的随机变量，其联合分 布不一定是二维正态分布，例如 令(X,)的联合密度函数为 f比，)=1。 -e 2 (1+sinxsiny), 2 显然，(X,Y)不服从正态分布但是 f()= 1-x 2e2,f0)=1e 2 √2 2π 因此边缘分布均为正态分布的随机变量，其联合分 布不一定是二维正态分布

(1 sin sin ), 2π 1 ( , ) ( , ) 2 2 2 f x y e x y X Y x y     令 的联合密度函数为 . 2 1 , ( ) 2 1 ( ) , ( , ) , 2 2 2 2 y Y x X f x e f y e X Y       显 然 不服从正态分布但 是 因此边缘分布均为正态分布的随机变量,其联合分 布不一定是二维正态分布. 边缘分布均为正态分布的随机变量,其联合分 布不一定是二维正态分布， 例如 §3.2 边缘分布

§3.2边缘分布 例设(X,Y)~f(x,y)= e',00时， fx(x)-[f(x,y)dy-Sedy=e". 当x≤0时， fx(x)=Jf(x,y)dy=0. x>0, 0, 其它

解 f x f x y y X ( ) ( , )d     e y x y d     f x f x y y X ( ) ( , )d     . x e   当 x  0时,  0.       0, . , 0, ( ) 其 它 故 e x f x x X (1) ( ); (2) { 1} . 0, . , 0 , ( , ) ~ ( , )          f x P X Y e x y X Y f x y X y 求 其 它 例 设 当x  0时, §3.2 边缘分布

§3.2边缘分布 (2)P{X+Y≤1} =J∬fx,J)dxdy y=1-x x+y≤1 -fidf"e7dy 1/2 -f le-0-e-Jdx =1+e1-2ei

(2) P{X Y  1}      x x y dx e y 1 2 1 0 d e e x x x [ ]d (1 ) 2 1 0        1 2 . 2 1 1     e  e f x y x y x y ( , )d d 1     y  x O x y y  1 x  1 2 §3.2 边缘分布

§3.2边缘分布 例2一整数N等可能地在1,2,3，.，10十个值中取 一个值.设D=D(N)是能整除N的正整数的个数， F=F(N)是能整除N的素数的个数试写出D和F 的联合分布律并求边缘分布律 解 样本点 12345678910 D 1223242434 F 0111121112 由此得D和F的联合分布律与边缘分布律：

解 1 2 3 4 5 6 7 8 9 10 1 2 2 3 2 4 2 4 3 4 0 1 1 1 1 2 1 1 1 2 例2 . . ( ) . . ( ) , 1,2,3, ,10 的联合分布律并求边缘分布律 是能整除 的素数的个数试写出 和 一个值 设 是能整除 的正整数的个数 一整数 等可能地在 十个值中取 F F N N D F D D N N N    由此得 D和F 的联合分布律与边缘分布律 : 样本点 D F §3.2 边缘分布

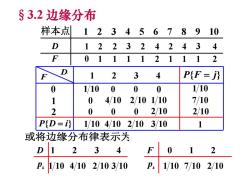
§3.2边缘分布 样本点 12 345678910 D 1223242434 F 01 11121112 D 23 4 P{F=} 0 1/10 0 0 0 1/10 1 04/10 2/101/10 7/10 2 0 0 0 2/10 2/10 P{D=} 1/104/102/103/10 1 或将边缘分布律表示为 23 4 F 2 P.1/104/102/103/10 P.1/107/102/10

D k p 1 2 3 4 1 10 4 10 2 10 3 10 F k p 0 1 2 1 10 7 10 2 10 1 2 3 4 1 10 0 0 0 0 4 10 2 10 1 10 0 0 0 2 10 D F P{F  j} 1 10 7 10 2 10 P{D  i} 1 10 4 10 2 10 3 10 1 或将边缘分布律表示为 1 2 3 4 5 6 7 8 9 10 1 2 2 3 2 4 2 4 3 4 0 1 1 1 1 2 1 1 1 2 样本点 D F 0 1 2 §3.2 边缘分布