电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第1章 预备知识 第2节 随机变量及其分布

随机地程及应用 精品课程 第1章第2节随机变量及其分布
第1章第2节 随机变量及其分布
随机变量及其分布 §1.2随机变量及其分布 一、随机变量 定义1.2.1设(2,F,P)是概率空间,X(o)是定义 在2上的单值实函数,若对于任意实数x∈R,有 {o:X(o)≤x}∈F, 称X(ω)是随机变量.。 可测空间 2,上的可 测函数 电子科技大学
随机变量及其分布 电子科技大学 §1.2 随机变量及其分布 一、随机变量 定义1.2.1 设(Ω,F, P)是概率空间, X(ω)是定义 在Ω上的单值实函数, 若对于任意实数x∈R, 有 {: X() x} F, 称X(ω)是随机变量. 可测空间 (Ω,F)上的可 测函数

随机变量及其分布 X是概率空间(2,F,P)上的随机变量,有 对于ω∈2,有唯一X(w)与之对应, 随机变量X 可理解为从 RxCR 样本空间2 X 到实数集Rx x=X() 的一个映射 电子科技大学
随机变量及其分布 电子科技大学 X是概率空间(Ω,F, P)上的随机变量, 有 对于ω∈Ω,有唯一X(ω)与之对应, ω X Ω RX R x=X(ω) 随机变量X 可理解为从 样本空间Ω 到实数集RX 的一个映射

随机变量及其分布 注{o:X(ω≤={X≤eF, 使P≤总有意义, 由随机变量定义及σ代数性质,有 十00 (X==(X≤x-U{X≤x-3∈f k=1 {Xx=-{X≤X}∈F,…· 电子科技大学
随机变量及其分布 电子科技大学 注 由随机变量定义及σ 代数性质, 有 } F 1 { } { } { 1 k k X x X x X x {X x} {X x} {X x} F {X x} Ω {X X} F, {ω:X(ω) x} {X x} F, 使P{X≤x}总有意义

随机变量及其分布 二、分布函数 定义1.2.2设X(o)是定义在概率空间(2, F,P)上的随机变量,令 F(x)=P{X≤x, Vx∈R 称Fx)为X的分布函数 对VM<b∈R,有P{a<X≤b}=F(b)-F(a), 性质 1)Fx)是单调不减函数; 电子科技大学
随机变量及其分布 电子科技大学 二、分布函数 定义1.2.2 设X(ω)是定义在概率空间(Ω, F, P)上的随机变量, 令 F(x) P{X x}, x R 称F(x) 为X 的分布函数. 对 a b R, 有 P{a X b} F(b) F(a), 1) F(x)是单调不减函数; 性质

随机变量及其分布 2)0≤F(x)≤1,limF(x)=0,limF(x)=1; X→-00 3)F心)是右连续函数,即对 x∈R,F(x+0)=F(x) 证3)由于Fx)单调不减,根据单调原理 仅需证,对任意的x∈R,有 -Fo 电子科技大学
随机变量及其分布 电子科技大学 2) 0 ( ) 1, lim ( ) 0, lim ( ) 1; F x F x F x x x 3) F(x)是右连续函数, 即对 x R, F(x 0) F(x). 证3)由于F(x)单调不减,根据单调原理 仅需证,对任意的x∈R, 有 ( ). 1 lim F x n F x n

随机变量及其分布 oo 因 ∩{X≤x+}={X≤x, n=] 2 且 X≤x+1}X≤x+23 D{X≤x+二}D… X x+1/2x+1 事件列X≤x+单调下降趋于≤,由概率 n 的连续性知性质3成立子科技大学
随机变量及其分布 电子科技大学 因 } { }, 1 { 1 X x n X x n } 1 { } 2 1 { 1} { n X x 且 X x X x ) …… ) ) x x+1/2 x+1 事件列 单调下降趋于{X≤x},由概率 的连续性知性质3成立. } 1 { n X x

随机变量及其分布 三、二维随机变量 定义1.2.3如果X和Y是定义在同一概率空 间(2,F,P)上的两个随机变量,称(X,Y)为二 维随机变量(向量). 思考 如何准确理解“维”的含义? 如何理解“定义在同一概率空间”? 电子科技大学
随机变量及其分布 电子科技大学 三、二维随机变量 定义1.2.3 如果X 和Y 是定义在同一概率空 间(Ω, F, P)上的两个随机变量, 称(X,Y )为二 维随机变量(向量). 如何准确理解“维”的含义? 如何理解“定义在同一概率空间” ? 思考:
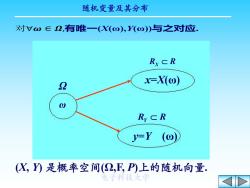
随机变量及其分布 对Vω∈2,有唯一(X(ω),Y(o)与之对应. RxCR 2 x-X(@) 0 Ry CR J=Y(@) (X,)是概率空间(2,F,P)上的随机向量. 电子科技大学
随机变量及其分布 电子科技大学 ω Ω x=X(ω) y=Y (ω) RX R RY R (X, Y) 是概率空间(Ω,F, P)上的随机向量

随机变量及其分布 Ex.1随机试验E:检查n个学生的健康情况,{心 表示抽检到第名学生,记样本空间为 2={1,2,…,n} 对于样本点∈2可定义 身高:X()会h, 体重:Y()会w. 身高X与体重Y构成定义在(2,可上的二维 随机变量(X,). EX2先抛一枚均匀硬币,再掷一颗均匀骰 子试验的样本空间为 电子科技大学
随机变量及其分布 电子科技大学 Ex.1 随机试验E: 检查n个学生的健康情况,{i} 表示抽检到第i 名学生,记样本空间为 Ω {1, 2,, n} 身高X与体重Y构成定义在(Ω, F)上的二维 随机变量(X, Y). EX.2 先抛一枚均匀硬币, 再掷一颗均匀骰 子试验的样本空间为
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第1章 预备知识 第1节 概率空间.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第0章 序言(覃思义).pdf
- 《模式识别》课程教学资源(书籍文献)Neural Networks for Classification - A Survey.pdf
- 《模式识别》课程教学资源(书籍文献)Learning in Linear Neural Networks - A Survey.pdf
- 《模式识别》课程教学资源(书籍文献)Artificial neural networks - a tutorial(Anil K. Jain、Jianchang Mao).pdf
- 《模式识别》课程教学资源(书籍文献)Data Clustering - 50 Years Beyond K-means.pdf
- 《模式识别》课程教学资源(书籍文献)Data Clustering - A Review(A.K. JAIN、M.N. MURTY、P.J. FLYNN).pdf
- 《模式识别》课程教学资源(书籍文献)A tutorial on Principal Components Analysis(Lindsay I Smith).pdf
- 《模式识别》课程教学资源(书籍文献)A Tutorial on Principal Component Analysis(Jonathon Shlens).pdf
- 《模式识别》课程教学资源(书籍文献)Sequential Minimal Optimization - A Fast Algorithm for Training Support Vector Machines(John C. Platt).pdf
- 《模式识别》课程教学资源(书籍文献)A Tutorial on Support Vector Machines for Pattern Recognition(CHRISTOPHER J.C. BURGES).pdf
- 《模式识别》课程教学资源(书籍文献)Introduction to Support Vector Learning.pdf
- 《模式识别》课程教学资源(书籍文献)TRENDS & CONTROVERSIES TRENDS & CONTROVERSIES - Support vector machines.pdf
- 《模式识别》课程教学资源(书籍文献)Background and Foreground Modeling Using Nonparametric Kernel Density Estimation for Visual Surveillance.pdf
- 《模式识别》课程教学资源(书籍文献)Tutorial on maximum likelihood estimation.pdf
- 《模式识别》课程教学资源(书籍文献)Statistical Pattern Recognition - A Review.pdf
- 《模式识别》课程教学资源(书籍文献)Digital Image Processing(Second Edition,Review Material,Rafael C. Gonzalez、Richard E. Woods).pdf
- 北京大学:《模式识别》课程教学资源(课件讲稿)人工神经网络简介.pdf
- 北京大学:《模式识别》课程教学资源(课件讲稿)非监督学习方法(第二部分).pdf
- 北京大学:《模式识别》课程教学资源(课件讲稿)非监督学习方法(第一部分).pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第1章 预备知识 第3节 随机变量的函数.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第1章 预备知识 第4节 随机变量的数字特征.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第1章 预备知识 第5节 特征函数.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第2章 随机过程的基本概念 第1节 随机过程的定义及分类.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第2章 随机过程的基本概念 第2节 随机过程的分布.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第2章 随机过程的基本概念 第3节 随机过程的数字特征.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第2章 随机过程的基本概念 第4节 随机过程的基本类型.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第3章几类重要随机过程 第1节 正态过程.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第3章几类重要随机过程 第2节 维纳过程.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第3章几类重要随机过程 第3节 泊松过程(一).pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第3章几类重要随机过程 第4节 泊松过程(二).pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第4章 二阶矩过程的均方微积分 第1节 收敛性与极限定理.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第4章 二阶矩过程的均方微积分 第2节 二阶矩随机变量空间及均方极限.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第4章 二阶矩过程的均方微积分 第3节 随机过程的均方极限与均方连续.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第4章 二阶矩过程的均方微积分 第4节 随机过程的均方导数.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第4章 二阶矩过程的均方微积分 第5节 随机过程的均方积分.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第5章 平稳随机过程 第1节 平稳随机过程的概念.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第5章 平稳随机过程 第2节 平稳过程的自相关函数.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第5章 平稳随机过程 第3节 平稳过程的各态历经性.pdf
- 电子科技大学:《随机过程及应用 Stochastic Processes and Applications》课程教学资源(课件讲稿)第5章 平稳随机过程 第4节 平稳过程的谱分析简介.pdf
