吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 52-5-5 §5 二次型及其标准型

三、用正交变换化二次型为标准型 经过上面的讨论,总结用正交变换化二次型为标准型 的一般步骤: 1将二次型r=∑∑a,xx,写成矩阵形式/=xA 2、由A-入E=0求出4的全部特征值: 3、由(A-2E)x=0,求出4的特征向量: 对于求出的不同的特征值所对应的特征向量已正交 只须单位化: 对于k重特征值入,所对应的k个线性无关的特征向量, 用Schimidt标准正交化方法把它们化为k个两两正交的单 位向量
三 、用正交变换化二次型为标准型 经过上面的讨论,总结用正交变换化二次型为标准型 的一般步骤: = = = = n i n j T f ai jxi xj f x Ax 1 1 1.将二次型 :写成矩阵形式 2 0, 、由 求出 的全部特征值: A E A − = 3 0 、由( ) ,求出 的特征向量; A E x A − = 对于求出的不同的特征值所对应的特征向量已正交, 只须单位化; 对于 重特征值 所对应的 个线性无关的特征向量, 用 标准正交化方法把它们化为 个两两正交的单 位向量。 k k λ k Schimidt k

4.把求出的个两两正交的单位向量,拼成正交矩 阵P,作正交变换x=Py 5用x=Py,把f化成标准型 f=y+见2y3++2ny 其中入,.…,n使f的矩阵4的n个特征值
2 2 2 2 2 1 1 n n f = y + y ++ y 1 2, , , 其中 使 的矩阵 的 个特征值。 λ λ λ f n n A 4.把求出的n个两两正交的单位向量,拼成正交矩 阵P,作正交变换x=Py; 5.用x=Py,把f 化成标准型

例2.求一个正交变换x=Py,把二次型 f=2xx2 +2xx;-2xx-2x2x+2x2x+2x3x 化为标准形 解1)二次型的矩阵为 三
例2. 求一个正交变换x=Py,把二次型 解 1)二次型的矩阵为 − − − − = 1 1 1 0 1 1 0 1 1 0 1 1 0 1 1 1 A 2 2 2 2 2 2 1 2 1 3 1 4 2 3 2 4 3 4 . f x x x x x x x x x x x x = + − − + + 化为标准形

2)由A-2E=0,求4的特征值 -入 A-E=
2)由A−E = 0,求A的特征值: − − − − − − = − 1 1 1 1 1 1 1 1 1 1 1 1 1 (1 ) 1 1 1 1 1 1 1 1 1 1 1 1 A E − − − − − = − − − − λ λ λ λ λ

-λ-1 -2 /1 =(1-2)20-元-1 -2 0-2-2-1 =(1-2)2(2+2入-3) =(1-2)2(2+3)(入-1)=0
0 0 0 1 0 2 1 2 0 1 2 2 1 1 1 1 (1 ) − + − − − − − − − = − 0 2 1 0 1 2 1 1 1 (1 ) 2 − − − = − − − − (1 ) ( 3)( 1) 0 (1 ) ( 2 3) 2 2 2 = − + − = = − + −

得A的特征值为 人=-3,九2=人=九4=1 3)由(A-入E)x=0,求A的特征向量 当=-3时,解方程(A+3E)三0.由 A+3E=
1 = −3, 2 = 3 = 4 = 1 得A的特征值为 − − − − − − − + = 1 1 1 3 1 1 3 1 1 3 1 1 1 1 1 1 ~ 1 1 1 3 1 1 3 1 1 3 1 1 3 1 1 1 A 3E − − − 0 0 0 0 0 0 4 4 0 1 1 0 1 1 1 1 ~ 0 2 2 4 0 2 2 0 0 2 2 0 1 1 1 1 ~ 1 3) 0, . 3 3 0. A E x A A E x − = = − + = 由( ) 求 的特征向量 当 时,解方程( ) 由 λ λ
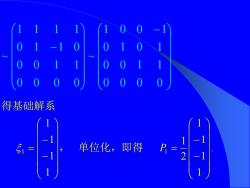
0 得基础解系 51 单位化,即得 1-2
− − 0 0 0 0 0 0 1 1 0 1 0 1 1 0 0 1 ~ 0 0 0 0 0 0 1 1 0 1 1 0 1 1 1 1 ~ . 1 1 1 1 2 1 1 1 1 1 1 1 − − = − − = , 单位化,即得 P 得基础解系
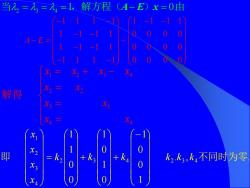
当入=入==1,解方程(A-E)x=0由 A-E= X 解得 X X: 0 即 k2.k3,k不同时为零 0
. , . 1 0 0 1 0 1 0 1 0 0 1 1 2 3 4 2 3 4 4 3 2 1 即 k k k k k k 不同时为零 x x x x − + + = 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 ~ 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 A E − − − − − − − = − − − − 1 2 3 4 2 2 3 3 4 4 x x x x x x x x x x = + − = = = 解得当 ,解方程( ) 由 234 = = = − = 1 0. A E x
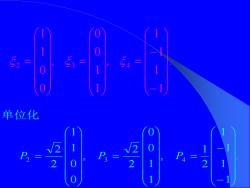
52 ! 单位化 2
. 1 1 1 1 , 1 1 0 0 , 0 0 1 1 2 3 4 − − = = = . 1 1 1 1 2 1 , 1 1 0 0 2 2 , 0 0 1 1 2 2 2 3 4 − − = = P = P P 单位化

4)于是正交变换为x=Py,即 X 为片片 5)用正交变换将f化成标准型 ∫=-3y+3+y+y 作业163页12题
3 . 5) 2 4 2 3 2 2 2 1 f y y y y f = − + + + 用正交变换将 化成标准型 作业 163页 12题. 1 1 2 2 3 3 4 4 4) , 1 1 1 0 2 2 2 1 1 1 0 2 2 2 1 1 1 0 2 2 2 1 1 1 0 2 2 2 x Py = − − = − − 于是正交变换为 即 x y x y x y x y
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 51-5-5 §5 二次型及其标准型.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 50-5-4 §4 对称矩阵的相似矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 49-5-4 §4 对称矩阵的相似矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 48-5-3 §3 相似矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 47-5-3 §3 相似矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 46-5-2 §2 方阵的特征值与特征向量.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 45-5-2 §2 方阵的特征值与特征向量.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 44-5-1 §1 向量的内积.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 43-5-1 §1 向量的内积.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 42-4-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 41-4-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 38-4-5 §5 向量空间.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 37-4-5 §5 向量空间.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 36-4-4 §4 向量组的秩.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 35-4-4 §4 向量组的秩.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 34-4-3 §3 线性相关性的判定.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 33-4-2-3 §2 向量组的线性相关性.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 32-4-1-2 §2 向量组的线性相关性.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 31-4-1-2 §1 n维向量.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 30-3-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 53-5-6-7 §6 用配方法化二次型为标准形.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 54-5-6-7 §7 用合同变换法化二次型为标准形.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 55-5-8 §8 正定二次型.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 56-5-8 §8 正定二次型.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 57-5-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 58-5-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)线性代数综合练习题1.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)线性代数综合练习题2.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)线性代数综合练习题3.ppt
- 中国科学技术大学:《组合数学》课程教学大纲(英文版)组合数学 Combinatorics(主讲:张先得).pdf
- 吉林大学:《计算方法》课程电子教案(PPT课件)数值方法绪论 Computing Method(主计:王新民).ppt
- 吉林大学:《计算方法》课程电子教案(PPT课件)第一章 插值方法 1.1 Lagrange插值公式.ppt
- 吉林大学:《计算方法》课程电子教案(PPT课件)第一章 插值方法 1.2 Newton插值多项式.ppt
- 吉林大学:《计算方法》课程电子教案(PPT课件)第一章 插值方法 1.3 Hermite插值.ppt
- 吉林大学:《计算方法》课程电子教案(PPT课件)第一章 插值方法 1.5 样条函数插值.ppt
- 吉林大学:《计算方法》课程电子教案(PPT课件)第二章 最佳平方逼近 2.1 正交多项式.ppt
- 吉林大学:《计算方法》课程电子教案(PPT课件)第二章 最佳平方逼近 2.2 最小二乘拟合多项式.ppt
- 吉林大学:《计算方法》课程电子教案(PPT课件)第二章 最佳平方逼近 2.3 一般最小二乘逼近问题的提法.ppt
- 吉林大学:《计算方法》课程电子教案(PPT课件)第三章 数值积分 3.1 数值积分法的三个基本问题.ppt
- 吉林大学:《计算方法》课程电子教案(PPT课件)第三章 数值积分 3.2 Newnon-Cotes型求积公式.ppt
