《计算机应用基础》课程教学资源（讲义）第九章 算法

目录 第九章算法2 9.12算法是计算机的灵魂. 2 9.1.3运行时间. 3 9.1.4算法的表示 9.2穷举算法 92.1百元百鸡. 9.2.2旅行商问题 9.3查找算法 9.3.1顺序查找 9.3.2二分查找 9.4排序算法 9.4.1直接插入排序」 9.4.2选择排序 9.4.3冒泡法排序. 9.4.4快速排序 9.45分而治之. 11 9.5贪婪算法 12 9.5.1教室调度问题 .12 9.5.2背包问题 .13 9.5.3旅行商问题. .13 9.6动态规划. 14 9.61背包问题. 15 9.6.2旅行商问题 .18 9.7回溯法. 9.8趣味算法举例. .21 9.8.1兔子产仔问题. .21 9.8.2谁在说谎 .22 9.8.3有趣的数字 .23

目录 第九章 算法. 2 9.1.2 算法是计算机的灵魂. 2 9.1.3 运行时间 . 3 9.1.4 算法的表示. 3 9.2 穷举算法. 4 9.2.1 百元百鸡 . 4 9.2.2 旅行商问题. 5 9.3 查找算法. 6 9.3.1 顺序查找 . 6 9.3.2 二分查找 . 6 9.4 排序算法. 7 9.4.1 直接插入排序. 7 9.4.2 选择排序 . 8 9.4.3 冒泡法排序. 9 9.4.4 快速排序 . 9 9.4.5 分而治之 . 11 9.5 贪婪算法. 12 9.5.1 教室调度问题. 12 9.5.2 背包问题 . 13 9.5.3 旅行商问题. 13 9.6 动态规划. 14 9.6.1 背包问题 . 15 9.6.2 旅行商问题. 18 9.7 回溯法 . 19 9.8 趣味算法举例. 21 9.8.1 兔子产仔问题. 21 9.8.2 谁在说谎 . 22 9.8.3 有趣的数字. 23

第九章算法 9.1算法简介 9.1.1引言 算法这个名词听上去很抽象，让人联想不到任何具体的物体。甚至你会觉得算法与自己的生活并无太多关联， 它只是为计算机专业人品成者科学家服各的。这样的相法直是大错特错了。 事实上，算法无处不在。比如你去食堂买饭会选择一个较短的队列，有的人则可能选择一个推进速度快的队列 再比如每天早上起床，你可能先读一会儿书再去吃早餐，而别的人可能先去吃早餐然后再看书。所有这些行为都是 算法的体现。运行这些算法并不一定是刻意的出现在你的意识中，也通常不会经过精心设计，但它确实存在。 1962年春天，宝洁公司发起了一场广告宣传活动，在应用数学家中引起了不小的反响.活动的重头戏是项竞赛， 奖金高达1万美元，在当时足以买下一座房子。参赛规则如下： 假设Tooy和Muldoon打算开车环游美国，地图上用点标出的33个地点都要游览，并且要走满足条件的路线 中最短的一条。请你为他们规划一条旅行路线，以伊利诺伊州的芝加哥市为旅途的起点和终点，依次用线连接各地 点，并使得总里程最短。 这就是著名的旅行商问题。这个问题容易求解吗？你可能会首先想到一个办法：检验每一条可能的路线，将最 短的一条记录下来寄给宝洁公司，然后坐等1万美元寄回家！这个策略简单又完美，但是，有一个潜在的困难：路 线总数是我们能够在有限的时间内检验完成的吗？ 我们用A 21 7 为这33个城市的编号，即A代表芝加哥市。由于旅行的起点和终点相同，每个排列对应 的路线实际都是一条环形路线，城市A为每条路线的起点，则第二座城市有32种可能选择，第三座城市有31种可 能选择，以此类推。最后，可以得到环形路线的总数为32×31×30××3×2×1。这个数字记作32，读作32的阶 乘。这个数字是多少呢？ 263130836933693530167218012160000000 这是无法完成的任务： 这里列出的只是解决旅行商问愿的其中一种方法。在后面的章节中，将会学习到更快捷的解决策略。可以这样 说，在算法的世界里，没有最快，只有更快！ 9.1.2算法是计算机的灵魂 说到这里，我们来了解本章的第一个概念，什么是算法？ 最常用的一个说法是：算法是解决间题的有穷步骤的描述 从这个定义中我们公现7洗是用类解决同题的也藏是说宜法发现总是由相的问要配动的，就拿推序米说 我们的生活中处处可 见次序 工作评优等 ,大家首先想到 方法是 概就是插入法了。换一个通俗易懂的说法，就是人们打牌时整理手中扑克牌的算法。这个算法的效率会随着数据量 的增加而大幅度降低，于是人们又发明了其他更快速的排序方法，这部分内容将在9.4节中详细介绍。 一个个新的算法都是为了解决前面算法遗留的问题而产生，新的算法提高了效率，同时也会有意或无意的引入 了新的问题，这应该就是算法永远不会停止发展的一个原因吧」 回到算法的定 我们还可以看出算法是求解问恩的步骤。由于计算机的计算操作完全是一步一步进行的，因 此算法的特征用于计算机是再合适不过了。计算机无法独立于算法而存在，如果说操作系统是计算机的心智，那么 算法就是计算机的灵魂。 举个例子，要计算1到100的累加和。有人先计算1+2，再将结果加上3，然后再将结果加上4，以此类推， 一直加到100。而有的人会将1+100，然后乘以50即可同样得出答案。这两种方法的时间复杂度是不一样的，很 显然第二种方法更快的得到答案。由于现代计算机运行速度都非常快，对于运行这样一点小运算来说不会有明显的 时间差异。但是在大型软件项目中，程序的执行效率高低就显得至关重要，会直接影响到用户体验。因此，合理的

第九章 算法 9.1 算法简介 9.1.1 引言 算法这个名词听上去很抽象，让人联想不到任何具体的物体。甚至你会觉得算法与自己的生活并无太多关联， 它只是为计算机专业人员或者科学家服务的。这样的想法真是大错特错了。 事实上，算法无处不在。比如你去食堂买饭会选择一个较短的队列，有的人则可能选择一个推进速度快的队列。 再比如每天早上起床，你可能先读一会儿书再去吃早餐，而别的人可能先去吃早餐然后再看书。所有这些行为都是 算法的体现。运行这些算法并不一定是刻意的出现在你的意识中，也通常不会经过精心设计，但它确实存在。 1962 年春天，宝洁公司发起了一场广告宣传活动，在应用数学家中引起了不小的反响。活动的重头戏是项竞赛， 奖金高达 1 万美元，在当时足以买下一座房子。参赛规则如下： 假设 Toody 和 Muldoon 打算开车环游美国，地图上用点标出的 33 个地点都要游览，并且要走满足条件的路线 中最短的一条。请你为他们规划一条旅行路线，以伊利诺伊州的芝加哥市为旅途的起点和终点，依次用线连接各地 点，并使得总里程最短。 这就是著名的旅行商问题。这个问题容易求解吗？你可能会首先想到一个办法：检验每一条可能的路线，将最 短的一条记录下来寄给宝洁公司，然后坐等 1 万美元寄回家！这个策略简单又完美，但是，有一个潜在的困难：路 线总数是我们能够在有限的时间内检验完成的吗？ 我们用 A~Z 及 1~7 作为这 33 个城市的编号，即 A 代表芝加哥市。由于旅行的起点和终点相同，每个排列对应 的路线实际都是一条环形路线，城市 A 为每条路线的起点，则第二座城市有 32 种可能选择，第三座城市有 31 种可 能选择，以此类推。最后，可以得到环形路线的总数为 32 x 31 x 30 x . x 3 x 2 x 1。这个数字记作 32!，读作 32 的阶 乘。这个数字是多少呢？ 263 130 836 933 693 530 167 218 012 160 000 000 这是无法完成的任务！ 这里列出的只是解决旅行商问题的其中一种方法。在后面的章节中，将会学习到更快捷的解决策略。可以这样 说，在算法的世界里，没有最快，只有更快！ 9.1.2 算法是计算机的灵魂 说到这里，我们来了解本章的第一个概念，什么是算法？ 最常用的一个说法是：算法是解决问题的有穷步骤的描述。 从这个定义中我们发现算法是用来解决问题的，也就是说算法的发现总是由相关的问题驱动的。就拿排序来说， 我们的生活中处处可见次序，比如考试排名，工作评优等。大家首先想到的排序方法是什么呢？这个问题的答案大 概就是插入法了。换一个通俗易懂的说法，就是人们打牌时整理手中扑克牌的算法。这个算法的效率会随着数据量 的增加而大幅度降低，于是人们又发明了其他更快速的排序方法，这部分内容将在 9.4 节中详细介绍。 一个个新的算法都是为了解决前面算法遗留的问题而产生，新的算法提高了效率，同时也会有意或无意的引入 了新的问题，这应该就是算法永远不会停止发展的一个原因吧。 回到算法的定义，我们还可以看出算法是求解问题的步骤。由于计算机的计算操作完全是一步一步进行的，因 此算法的特征用于计算机是再合适不过了。计算机无法独立于算法而存在，如果说操作系统是计算机的心智，那么 算法就是计算机的灵魂。 举个例子，要计算 1 到 100 的累加和。有人先计算 1+ 2 ，再将结果加上 3，然后再将结果加上 4，以此类推， 一直加到 100。而有的人会将 1 + 100，然后乘以 50 即可同样得出答案。这两种方法的时间复杂度是不一样的，很 显然第二种方法更快的得到答案。由于现代计算机运行速度都非常快，对于运行这样一点小运算来说不会有明显的 时间差异。但是在大型软件项目中，程序的执行效率高低就显得至关重要，会直接影响到用户体验。因此，合理的

算法设计是非常必要的。 9.1.3运行时间 上面讲到的1累加到100的例子中.我们提到了“时间复杂度”这个概今，这一节我们就详细的了解一下有关 算法的运行时间问题。 假设在字典中查找一个以M开头的单词，你可以从头开始翻页，直到进入以M开头的部分。但是我可以肯定 你不会这样做的。你会从中间开始，因为你知道M开头的单词在字典的中间位置附近。这两种查找的方法就存在 一个运行时间上的差异。一般而言，效率越高的算法就越能在最大限度上减少运行时间或占用的空间。 再比如有100个数字，己经按照从小到大的顺序排列好了。当我们需要找出其中某一个数字时，可以从头开始 比对，最差的情况是需要比对100次。那么我们也试着从中间开始，也就是说，先比对这组数列中间的那个数字是 不是我们需要的，如果不是，就判 一下这个中间的数字比我们需要的数字大了还是小了？如果大，就从中间数气 的右侧列表中继续查找，如果小，就从中间数字的左侧列表中继续查找。对100个数字而言，这种方法最多需要比 对7次。如果列表中包含40亿个数字，最多也只需要比对32次。厉害吧？ 对长度为n的列表，使用逐个比对的方法就需要执行n次操作，这个运行时间我们记做0()，也叫线性时间。 如果使用从中间折半的方法就仅仅需要执行1ogn次操作，记做0(gn),也叫对数时间。这种表示法不是以秒为单 位的，它告诉我们算 到底有多快，也就是指出了算法运行时间的增速。Og)此O)快，当需要搜索的元素越多 时，前者比后者快的越多 9.1.4算法的表示 不管用什么形式描述一个解决问题的过程，只要它逻辑清晰，结果正确，哪怕只是在脑子里构思的，也都是好 算法。对于复杂问题的解决，单靠脑子构思可能就不够了，这就需要借助一些工具来表示解决过程。算法的表示形 式很多，下面列出几种常用的方式以供参考。 1.自然语言 知道把大象放冰箱一共分几步吗？一，把冰箱门打开。二，把大象塞进去。三，把冰箱门关上。这就是用自然 语言描述的算法。 下面我们来看一个真正的算法：欧几里得算法。古希腊数学家欧几里得（公元前3世纪）曾在他的著作中描述 过求两个数的最大公因子的过程。这里用到了一个定理，即两个整数的最大公约数等于其中较小的那个数和两数相 除余数的最大公约数。 算法9.1 ()输入任意两个整数m和n,使得m>n: 2)计算：m除以n得余数r: (3)若r=0,则n为求得的最大公约数，算法结束：否则执行(4： 4)将m的值修改为 将n的值修政为r,再重复执行(2) 这就是用自然语言描述的算法。当然，除了这种很简单的问题，一般是不使用自然语言来描述计算机算法的， 因为自然语言存在二义性，表达起来不精准。 2.流程图 流程图是一种使用最普遍的算法表示方法，它用一组标准图形符号来描述算法。它的主要优点是简单直观， 便于理解。图9.1给出了流程图的图元表示方法。前面介绍的欧几里得算法也可以用流程图来表示，如图9.2所示

算法设计是非常必要的。 9.1.3 运行时间 上面讲到的 1 累加到 100 的例子中，我们提到了“时间复杂度”这个概念，这一节我们就详细的了解一下有关 算法的运行时间问题。 假设在字典中查找一个以 M 开头的单词，你可以从头开始翻页，直到进入以 M 开头的部分。但是我可以肯定， 你不会这样做的。你会从中间开始，因为你知道 M 开头的单词在字典的中间位置附近。这两种查找的方法就存在 一个运行时间上的差异。一般而言，效率越高的算法就越能在最大限度上减少运行时间或占用的空间。 再比如有 100 个数字，已经按照从小到大的顺序排列好了。当我们需要找出其中某一个数字时，可以从头开始 比对，最差的情况是需要比对 100 次。那么我们也试着从中间开始，也就是说，先比对这组数列中间的那个数字是 不是我们需要的，如果不是，就判断一下这个中间的数字比我们需要的数字大了还是小了？如果大，就从中间数字 的右侧列表中继续查找，如果小，就从中间数字的左侧列表中继续查找。对 100 个数字而言，这种方法最多需要比 对 7 次。如果列表中包含 40 亿个数字，最多也只需要比对 32 次。厉害吧？ 对长度为 n 的列表，使用逐个比对的方法就需要执行 n 次操作，这个运行时间我们记做 O(n)，也叫线性时间。 如果使用从中间折半的方法就仅仅需要执行 log n 次操作，记做 O(log n)，也叫对数时间。这种表示法不是以秒为单 位的，它告诉我们算法到底有多快，也就是指出了算法运行时间的增速。O(log n)比 O(n)快，当需要搜索的元素越多 时，前者比后者快的越多。 9.1.4 算法的表示 不管用什么形式描述一个解决问题的过程，只要它逻辑清晰，结果正确，哪怕只是在脑子里构思的，也都是好 算法。对于复杂问题的解决，单靠脑子构思可能就不够了，这就需要借助一些工具来表示解决过程。算法的表示形 式很多，下面列出几种常用的方式以供参考。 1. 自然语言 知道把大象放冰箱一共分几步吗？一，把冰箱门打开。二，把大象塞进去。三，把冰箱门关上。这就是用自然 语言描述的算法。 下面我们来看一个真正的算法：欧几里得算法。古希腊数学家欧几里得（公元前 3 世纪）曾在他的著作中描述 过求两个数的最大公因子的过程。这里用到了一个定理，即两个整数的最大公约数等于其中较小的那个数和两数相 除余数的最大公约数。 算法 9.1： (1) 输入任意两个整数 m 和 n，使得 m>n； (2) 计算：m 除以 n 得余数 r； (3) 若 r=0，则 n 为求得的最大公约数，算法结束；否则执行(4)； (4) 将 m 的值修改为 n，将 n 的值修改为 r，再重复执行(2)。 这就是用自然语言描述的算法。当然，除了这种很简单的问题，一般是不使用自然语言来描述计算机算法的， 因为自然语言存在二义性，表达起来不精准。 2. 流程图 流程图是一种使用最普遍的算法表示方法，它用一组标准图形符号来描述算法。它的主要优点是简单直观， 便于理解。图 9.1 给出了流程图的图元表示方法。前面介绍的欧几里得算法也可以用流程图来表示，如图 9.2 所示

开始 起止框 输入m和m rm%n 输入输出框 条件判断 处理语句框 流程线 结束门 图9.1流程图的图元 图9.2欧几里得算法流程图 9.2穷举算法 穷举算法是一种最为直接、实现最简单、最耗时的一种算法思想。它的基本思想是：在可能的解空间中穷举出 每一种可能的解，并对每一个可能解进行判断，从中筛选出问题的答案。 9.2.1百元百鸡 公元5世纪末，我国古代数学家张丘建在他编写的《算经》中提出这样一个问题：“鸡 一值钱五：鸡母一值 钱三：鸡雏三值钱一。百钱买百鸡，问鸡翁、母、雏各几何？”意思是说，公鸡每只5元，母鸡每只3元，3只小 鸡1元，用100元钱买100只鸡，求公鸡、母鸡和小鸡各多少只。这里设每种鸡至少一只。 算法分析： 我们假设公鸡、母鸡、小鸡的只数分别为x、y2。我们以三种鸡总数(x+y+z)和买鸡的总钱数(5x+3y+z3) 都等于100为判定条件，穷举出各种鸡的只数 算法9.2： 公鸡数x=1to100 /公鸡数从1枚举到100 母鸡数y1to100 /母鸡数从1枚举到100 小鸡数=1to100 ∥小鸡数从1枚举到100 如果ky4z10并且5x43y+z/3100那么 输出×、y、z的但 这个算法对×、yz都从1开始枚举到100，计算机需要做100*100*100次比较操作，虽然这点“规模”对计 算机来说不算什么，可以很快完成计算，但是，这个算法仍然后很大的改进空间。 因为公鸡5元钱一只，所以100元最多买20只公鸡。同理，100元最多买33只母鸡，而小鸡的数目是100-xy, 因此没必要枚举。改进后的算法如下： 算法93： 公鸡数x=1to20 公鸡数从1枚举到20 母鸡数y1to33/∥母鸡数从1枚举到33 小鸡数2=100-xy 如果(5*x+3y+z/3=100那么 出 、z的值 改进后的算法让计算机执行操作的次数减少到大约660次。这个程度的优化在实际运行中是感觉不到的。但是 算法优化的思想还请读者记在心里

图 9.1 流程图的图元 图 9.2 欧几里得算法流程图 9.2 穷举算法 穷举算法是一种最为直接、实现最简单、最耗时的一种算法思想。它的基本思想是：在可能的解空间中穷举出 每一种可能的解，并对每一个可能解进行判断，从中筛选出问题的答案。 9.2.1 百元百鸡 公元 5 世纪末，我国古代数学家张丘建在他编写的《算经》中提出这样一个问题：“鸡翁一值钱五；鸡母一值 钱三；鸡雏三值钱一。百钱买百鸡，问鸡翁、母、雏各几何？”意思是说，公鸡每只 5 元，母鸡每只 3 元，3 只小 鸡 1 元，用 100 元钱买 100 只鸡，求公鸡、母鸡和小鸡各多少只。这里设每种鸡至少一只。 算法分析： 我们假设公鸡、母鸡、小鸡的只数分别为 x、y、z。我们以三种鸡总数（x+y+z）和买鸡的总钱数（5*x+3*y+z/3） 都等于 100 为判定条件，穷举出各种鸡的只数。 算法 9.2： 公鸡数 x=1 to 100 //公鸡数从 1 枚举到 100 母鸡数 y=1 to 100 //母鸡数从 1 枚举到 100 小鸡数 z=1 to 100 //小鸡数从 1 枚举到 100 如果(x+y+z)=100 并且 (5*x+3*y+z/3)=100 那么 输出 x、y、z 的值 这个算法对 x、y、z 都从 1 开始枚举到 100，计算机需要做 100*100*100 次比较操作，虽然这点“规模”对计 算机来说不算什么，可以很快完成计算，但是，这个算法仍然后很大的改进空间。 因为公鸡 5 元钱一只，所以 100 元最多买 20 只公鸡。同理，100 元最多买 33 只母鸡，而小鸡的数目是 100-x-y， 因此没必要枚举。改进后的算法如下： 算法 9.3： 公鸡数 x=1 to 20 //公鸡数从 1 枚举到 20 母鸡数 y=1 to 33 //母鸡数从 1 枚举到 33 小鸡数 z=100-x-y 如果 (5*x+3*y+z/3)=100 那么 输出 x、y、z 的值 改进后的算法让计算机执行操作的次数减少到大约 660 次。这个程度的优化在实际运行中是感觉不到的。但是 算法优化的思想还请读者记在心里

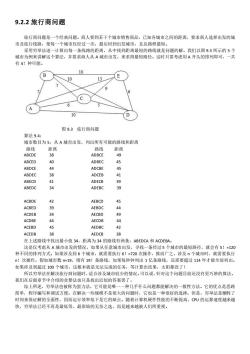
9.2.2旅行商问题 旅行商问愿是一个经典问题。商人要到若干个城市销售商品，己知各城市之间的距离，要求商人选择出发的城 市及旅行线路，使每一个城市仅经过一次，最后回到出发城市 ,且总路程最短 采用穷举法逐一计算出每一条线路的距离，从中找到距离最短的路线就是问题的解。我们以图9.3所示的5个 城市为例来讲解这个算法，并要求商人从A城市出发，来求得最短路径。这时只需考虑用A开头的排列即可，一共 有4！种可能。 10 B 10 A 10 D 图9.3旅行商问题 算法9.4： 城市数目为5，从A城市出发，列出所有可能的路线和距离 ABCED ADBEC 45 ABDCE 名 ADCBE 45 ABDEC ADCEB 41 ABECD ADECB 3 ABEDC ADEBC ACBDE AEBCD 45 ACBED AEBDC 44 ACDEB AECBD 49 ACDBE ACEBD 1445 14 ACEDB 38 AEDCB 38 在上述路线中找出最小值34，距离为34的路线有两条：ABEDCA和ACDEBA。 这是仅考虑从A城市出发的情况，如果从任意城市出发，寻找一条经过5个城市的最短路径，就会有5！=120 种不同的排列方式。如果涉及到6个城市，就需要执行6：720次操作，推而广之，涉及n个城市时，就需要执行 n!次操作。假如城市数=19，则有19：条路线，如果每秒钟列出1亿条路线，还需要超过114年才能全部列出。 如果涉及到超过100个城市，这根本就是无法完成的任务，等计算出结果，太阳都没了！ 所以穷举法在解决旅行商问题时，适合涉及城市较少的情况。可以说，针对这个问题目前还没有更巧妙的算法。 我们在后面章节中介绍的贪婪法也只是找出近似的答案罢了。 综上所述，穷举法也被称为童力法，它可能是唯一一种几乎什么问题都能解决的一般性方法。它的优点是思路 简单，程序编写和调试方便。在解决 些规模不是很大的问题时 它也是 种很好的选择。但是， 穷举法是牺牲 时间来保证解的全面性，因而运行效率低下是它的缺点。随着计算机硬件性能的不断提高，CU的运算速度越来越 快，穷举法已经不再是最低等、最原始的无奈之选，而是越来越被人们所重视

9.2.2 旅行商问题 旅行商问题是一个经典问题。商人要到若干个城市销售商品，已知各城市之间的距离，要求商人选择出发的城 市及旅行线路，使每一个城市仅经过一次，最后回到出发城市，且总路程最短。 采用穷举法逐一计算出每一条线路的距离，从中找到距离最短的路线就是问题的解。我们以图 9.3 所示的 5 个 城市为例来讲解这个算法，并要求商人从 A 城市出发，来求得最短路径。这时只需考虑用 A 开头的排列即可，一共 有 4！种可能。 图 9.3 旅行商问题 算法 9.4： 城市数目为 5，从 A 城市出发，列出所有可能的路线和距离 路线 距离 路线 距离 ABCDE 38 ADBCE 49 ABCED 40 ADBEC 45 ABDCE 44 ADCBE 45 ABDEC 38 ADCEB 41 ABECD 41 ADECB 39 ABEDC 34 ADEBC 39 ACBDE 42 AEBCD 45 ACBED 39 AEBDC 44 ACDEB 34 AECBD 49 ACDBE 44 AECDB 44 ACEBD 45 AEDBC 42 ACEDB 38 AEDCB 38 在上述路线中找出最小值 34，距离为 34 的路线有两条：ABEDCA 和 ACDEBA。 这是仅考虑从 A 城市出发的情况，如果从任意城市出发，寻找一条经过 5 个城市的最短路径，就会有 5！=120 种不同的排列方式。如果涉及到 6 个城市，就需要执行 6！=720 次操作，推而广之，涉及 n 个城市时，就需要执行 n！次操作。假如城市数 n=19，则有 19！条路线，如果每秒钟列出 1 亿条路线，还需要超过 114 年才能全部列出。 如果涉及到超过 100 个城市，这根本就是无法完成的任务，等计算出结果，太阳都没了！ 所以穷举法在解决旅行商问题时，适合涉及城市较少的情况。可以说，针对这个问题目前还没有更巧妙的算法。 我们在后面章节中介绍的贪婪法也只是找出近似的答案罢了。 综上所述，穷举法也被称为蛮力法，它可能是唯一一种几乎什么问题都能解决的一般性方法。它的优点是思路 简单，程序编写和调试方便。在解决一些规模不是很大的问题时，它也是一种很好的选择。但是，穷举法是牺牲了 时间来保证解的全面性，因而运行效率低下是它的缺点。随着计算机硬件性能的不断提高，CPU 的运算速度越来越 快，穷举法已经不再是最低等、最原始的无奈之选，而是越来越被人们所重视

9.3查找算法 查找算法与我们的生活息息相关。比如从书架上找一本书，从字典中找某一个单词，甚至在使用计算机登录你 的社交账号时，都用到了查找算法。 9.3.1顺序查找 查找算法中最简单的方法是顺序查找。也就是从第一个开始，逐个查找，比对，直到找到所需数据为止。比如 从书架上找一本书这个例子，如果所有的书都是随机放置在书架上的怎么会这样？)，那么就没有好办法了，只能 使用顺序查找的方式，一本一本的翻阅。很显然，这是效率非常低的一种查找方式。但是它胜在简单直观，对于规 模不大的数据的查找，这也是最容易实现的方法。 下面我们来做 个游戏。 我随便想一个介于1到100之间的数字，请你猜出我想到的这个数字。现在使用顺序查找法，那么你需要从1 开始往后猜。 你：1我：小了 你：2 我：小了 你：3 我：小了 你：4 我：小了 如果我想的数字是99，那么你需要猜99次才能猜到！下面是一种更好的猜数方法。 9.3.2二分查找 你：50 我：小了 /这时可以排除掉一半的数字，只需猜大于50的数字 你：75 我.大了 这时又排除掉一半的数字，只需在50到75之间选择 你：63 我：大了 /这时又排除掉一半的数字，只需在50到63之间选择 你：57 我：对门了！ 这就是二分查找法。不管我心里想的是什么数字，你都可以在7次以内猜到。 如果要从一本字典中查找单词，该字典包含240000个单词，而要找的单词恰好在字典的末尾。那么，如果使 用顺序查找，则需要240000步操作，使用二分查找，每次都排除一半单词，直到最后只剩下一个，只需18步操作。 这两种算法的效率高低一目了然。 般而言，对于包含n个元素的列表，用顺序查找最多需要n步，用二分查找最 多周要logzn步 当然，只有当列表中的数据有序时，二分查找才管用。因此，排序是查找的前提，有关排序的内容我们将在9.4 节中详细介绍。 下面通过一个实倒来给出二分查找的算法描述 -19 2732 4467081 92 这组数据已按从小到大的顺序排列好，我们要查找81这个数字，如果存在，给出它的位置，如果不存在，给 出相应的提示信总。 算法分析： 第1次比较的数字范围是整个数字序列，如图94中第一行数字下的框线所示。首先找到全部数字的中间位置， 也就是34，它将数字序列一分为二 要找的数字81>34，因此，继续在后半部分查找。此时要查找的数字范围是 34后面一个数字开始的，如图9.4中第二行数字下的框线所示，问题规模减小了一半。第2次比较的中间位置是数 字70，要找的数字81>70，则在后半部分继续查找。第3次比较的中间位置是数字81，至此查找成功

9.3 查找算法 查找算法与我们的生活息息相关。比如从书架上找一本书，从字典中找某一个单词，甚至在使用计算机登录你 的社交账号时，都用到了查找算法。 9.3.1 顺序查找 查找算法中最简单的方法是顺序查找。也就是从第一个开始，逐个查找，比对，直到找到所需数据为止。比如 从书架上找一本书这个例子，如果所有的书都是随机放置在书架上的(怎么会这样？)，那么就没有好办法了，只能 使用顺序查找的方式，一本一本的翻阅。很显然，这是效率非常低的一种查找方式。但是它胜在简单直观，对于规 模不大的数据的查找，这也是最容易实现的方法。 下面我们来做一个游戏。 我随便想一个介于 1 到 100 之间的数字，请你猜出我想到的这个数字。现在使用顺序查找法，那么你需要从 1 开始往后猜。 你：1 我：小了 你：2 我：小了 你：3 我：小了 你：4 我：小了 . . 如果我想的数字是 99，那么你需要猜 99 次才能猜到！下面是一种更好的猜数方法。 9.3.2 二分查找 你：50 我：小了 //这时可以排除掉一半的数字，只需猜大于 50 的数字 你：75 我：大了 //这时又排除掉一半的数字，只需在 50 到 75 之间选择 你：63 我：大了 //这时又排除掉一半的数字，只需在 50 到 63 之间选择 你：57 我：对了！ 这就是二分查找法。不管我心里想的是什么数字，你都可以在 7 次以内猜到。 如果要从一本字典中查找单词，该字典包含 240000 个单词，而要找的单词恰好在字典的末尾。那么，如果使 用顺序查找，则需要 240000 步操作，使用二分查找，每次都排除一半单词，直到最后只剩下一个，只需 18 步操作。 这两种算法的效率高低一目了然。一般而言，对于包含 n 个元素的列表，用顺序查找最多需要 n 步，用二分查找最 多需要 log2n 步。 当然，只有当列表中的数据有序时，二分查找才管用。因此，排序是查找的前提，有关排序的内容我们将在 9.4 节中详细介绍。 下面通过一个实例来给出二分查找的算法描述。 假定有一组数据如下： -19 6 27 32 34 46 70 81 92 这组数据已按从小到大的顺序排列好，我们要查找 81 这个数字，如果存在，给出它的位置，如果不存在，给 出相应的提示信息。 算法分析： 第 1 次比较的数字范围是整个数字序列，如图 9.4 中第一行数字下的框线所示。首先找到全部数字的中间位置， 也就是 34，它将数字序列一分为二。要找的数字 81>34，因此，继续在后半部分查找。此时要查找的数字范围是从 34 后面一个数字开始的，如图 9.4 中第二行数字下的框线所示，问题规模减小了一半。第 2 次比较的中间位置是数 字 70，要找的数字 81>70，则在后半部分继续查找。第 3 次比较的中间位置是数字 81，至此查找成功

第1次比较：-19627323446708192 第2次比：1962”324601明 第3次比较：196273234467092 图9.4二分查找过程 算法9.5 (1)将n个有序数字保存在变量a)中，i1n 要查找的关键字保存在变量key中 (2使用两个变量low和high分别代表要查找范围的下限和上限。显然它们的初值分别是：Iow=1,high=n(n 为全部数字的个数) 3如果 w<high,计算中间位置用变量mid保存：mid=(ow+high/2(如果无法整除，则取小于它的最大整数) 然后给变量y赋值：ya(mid,转向4 如果low≥high,转向7)。 (4如果ykey,则转向(6)。否则，转向5)。 6)输出k (7)榆出提示信息：没有要查找的数字。 9.4排序算法 9.4.1直接插入排序 直接插入排序是一种最为简单的排序方法。它的基本思想是将一条数据插入到已排好的有序表中合适的位置 使得插入后的序列仍然有序。下面通过 个例子来介绍直接插入排序的执行过程。 有这样一个数据元素序列 {13,6,7.2.11.9,28,4} 该序列的第一个元素13是初始子序列，下面要将元素6插入到这个子序列中，得到一个包含两个元素的有序 子序列。怎么操作呢？首先确定6要插入的位置。具体方法是，从13开始向左查找，由于6小于13，因此要将13 向后移动，将6插入到13的前面。这个过程被称为一直接插入排序。 这时数据序列变为了 {(6,13),7,2.11,9,28,4} 下面我们继续将元素7插入到有序子序列中。具体方法是，从13开始向左查找，由于7小于13，因此13要继 续向后移动：又因为7大于6，因此7要插入到6和13之间。这样就在原序列中得到一个新的包含3个元素的有序 子序列。 {6,7,13,2,11,9,28,4 按照这种插入的方法，可将后面的5个元素逐一插入到前面的子序列中，当子序列与原序列长度一样时，插入 排序结束。下面是元素序列13,6,7,2,11,9,28,4的直接插入排序全过程。 初始状态： {13,5,7,2,11,9,28,4 第1趟直接插入排序：(6,13，2,11,9,28,4 第2趙直接插入排序：(6,7,13一2,11,9,28,4

图 9.4 二分查找过程 算法 9.5： (1)将 n 个有序数字保存在变量 a(i)中，i=1.n 要查找的关键字保存在变量 key 中 (2)使用两个变量 low 和 high 分别代表要查找范围的下限和上限。显然它们的初值分别是：low=1，high=n（n 为全部数字的个数） (3)如果 lowkey，则修改 high 的值：high=mid-1，转向(3)。 (6)输出 k。 (7)输出提示信息：没有要查找的数字。 9.4 排序算法 9.4.1 直接插入排序 直接插入排序是一种最为简单的排序方法。它的基本思想是将一条数据插入到已排好的有序表中合适的位置， 使得插入后的序列仍然有序。下面通过一个例子来介绍直接插入排序的执行过程。 有这样一个数据元素序列 {13, 6, 7, 2, 11, 9, 28, 4} 该序列的第一个元素 13 是初始子序列，下面要将元素 6 插入到这个子序列中，得到一个包含两个元素的有序 子序列。怎么操作呢？首先确定 6 要插入的位置。具体方法是，从 13 开始向左查找，由于 6 小于 13，因此要将 13 向后移动，将 6 插入到 13 的前面。这个过程被称为一趟直接插入排序。 这时数据序列变为了 { (6, 13), 7, 2, 11, 9, 28, 4} 下面我们继续将元素 7 插入到有序子序列中。具体方法是，从 13 开始向左查找，由于 7 小于 13，因此 13 要继 续向后移动；又因为 7 大于 6，因此 7 要插入到 6 和 13 之间。这样就在原序列中得到一个新的包含 3 个元素的有序 子序列。 { (6, 7, 13), 2, 11, 9, 28, 4} 按照这种插入的方法，可将后面的 5 个元素逐一插入到前面的子序列中，当子序列与原序列长度一样时，插入 排序结束。下面是元素序列{13, 6, 7, 2, 11, 9, 28, 4}的直接插入排序全过程。 初始状态： { (13), 6, 7, 2, 11, 9, 28, 4} 第 1 趟直接插入排序：{ (6, 13), 7, 2, 11, 9, 28, 4} 第 2 趟直接插入排序：{ (6, 7, 13), 2, 11, 9, 28, 4}

第3趙直接插入排序：(2,67,13)1,9,28,4 第4植直接插入排序：（亿，6,7，止13助9,28,4 第5趟直接插入排序：{2,6,7,911,13引，28,4 第6趟直接插入排序：(2,6,7,9,11,13,28,4 第7趟直接插入排序：(2,46,7,9.11,13,28} 从这个插入排序的过程中可以看出：一个包含有n个元素的序列，需要1趟排序就可以将原序列排列有序。 显然这个算法的效率是偏低的。 9.4.2选择排序 选择排序是一种常见的排序方法，下面通过一个实例来了解它的排序原理。有这样一组数据元素(13,6 2,11,9,28,4,第一趟排序时，要从这8个元素中找出最小的那个，也就是序列中的元素2，将它与第一个 元素13交换位置。得到序列： 【(2).6.7,13.11.9.28.4} 第二趟排序时，从后面的7个元素中找到最小的元素4，将它与第二个元素交换位置，得到序列： {2,47, 13,11,9,28,6 第三趟排序时，从后面的6个元素中找到最小的元素6，将它与第三个元素交换位置，得到序列： {2,4h,613,11,9,28,71 接下来的每一趟排序操作都是按照这样的“找最小值再交换位置”的方法进行。上述元素序列的选择排序过程 如下 初始状态： {136,7,2.11,9,28,4 第1趟选择排序：{26,7,13,11,9,28，_4 第2趙选择排序：{亿，4,7,13,11,9,286} 第3趟选择排序：{2,4,61,13,11,9,28,7 第4描选择排序：{(2,46,7八，11,9,28,13引 第5脑选择排序：，46,79立28,13 第6趟选择排序：{2,4,6,7,9,11.2迟13引 第7趟选择排序：{2,4,6,7,911,1328 从这个选择排序的过程中可以看出：一个包含有n个元素的序列，需要1趟排序就可以将原序列排列有序 最后第n个元素不需要再选择，它一定是最大的 与插入排序相比较，选择排序的优点是移动数据的次数已知(1次)，缺点是比较次数较多。而插入排序的 缺点是比较次数不一定，插入点后的数据移动较多，当数据总量庞大的时候，这个操作还是比较费时的

第 3 趟直接插入排序：{ (2, 6, 7, 13), 11, 9, 28, 4} 第 4 趟直接插入排序：{ (2, 6, 7, 11, 13), 9, 28, 4} 第 5 趟直接插入排序：{ (2, 6, 7, 9, 11, 13), 28, 4} 第 6 趟直接插入排序：{ (2, 6, 7, 9, 11, 13, 28), 4} 第 7 趟直接插入排序：{ (2, 4, 6, 7, 9, 11, 13, 28) } 从这个插入排序的过程中可以看出：一个包含有 n 个元素的序列，需要 n-1 趟排序就可以将原序列排列有序。 显然这个算法的效率是偏低的。 9.4.2 选择排序 选择排序是一种常见的排序方法，下面通过一个实例来了解它的排序原理。有这样一组数据元素 { 13, 6, 7, 2, 11, 9, 28, 4}，第一趟排序时，要从这 8 个元素中找出最小的那个，也就是序列中的元素 2，将它与第一个 元素 13 交换位置。得到序列： { (2), 6, 7, 13, 11, 9, 28, 4} 第二趟排序时，从后面的 7 个元素中找到最小的元素 4，将它与第二个元素交换位置，得到序列： { (2, 4), 7, 13, 11, 9, 28, 6} 第三趟排序时，从后面的 6 个元素中找到最小的元素 6，将它与第三个元素交换位置，得到序列： { (2, 4), 6, 13, 11, 9, 28, 7} 接下来的每一趟排序操作都是按照这样的“找最小值再交换位置”的方法进行。上述元素序列的选择排序过程 如下： 初始状态： { 13, 6, 7, 2, 11, 9, 28, 4} 第 1 趟选择排序：{ (2), 6, 7, 13, 11, 9, 28, 4} 第 2 趟选择排序：{ (2, 4), 7, 13, 11, 9, 28, 6} 第 3 趟选择排序：{ (2, 4, 6), 13, 11, 9, 28, 7} 第 4 趟选择排序：{ (2, 4, 6, 7), 11, 9, 28, 13} 第 5 趟选择排序：{ (2, 4, 6, 7, 9), 11, 28, 13} 第 6 趟选择排序：{ (2, 4, 6, 7, 9, 11), 28, 13} 第 7 趟选择排序：{ (2, 4, 6, 7, 9, 11, 13), 28} 从这个选择排序的过程中可以看出：一个包含有 n 个元素的序列，需要 n-1 趟排序就可以将原序列排列有序。 最后第 n 个元素不需要再选择，它一定是最大的。 与插入排序相比较，选择排序的优点是移动数据的次数已知（n-1 次），缺点是比较次数较多。而插入排序的 缺点是比较次数不一定，插入点后的数据移动较多，当数据总量庞大的时候，这个操作还是比较费时的

9.4.3冒泡法排序 目泡排序法的思想比较简单，对于个元素，从第一个开始依次比较相邻的两个，如果是逆序就交换它们的位 置。重复多次以后 最大（或最小）的元素就“沉到”列表的最后 个位置。第 遍操作将第二大（或小）的元 沉下去，这样一直操作，直到1遍后，列表就排好序了。我们以10个数字的升序排列为例讲解这个算法， 算法分析： 首先将第1个数字和第2个数字进行比较，若为逆序（即第1个数字大于第2个数字），则交换两个变量的值。 然后比较第2个数字和第3个数字的值，若为逆序则交换之。依次类推，直到第9个和第10个数字比较完为止 这个过程称为第一墙冒泡排序，其结果是将最大的数字转移到最后一个位置上。然后进行第二趟目泡排序，对前 个数字进行同样操作，将第 大的数字转移到第九个数字的位置。这样的冒泡排序一共需要进行9趟。由此得到 法9.5。图93展示了骨泡排序的一个实例，从图中可以看出，在冒泡排序的过程中，小的数字好比水中的气泡逐湖 向上漂浮，大的数字就像石块一样逐渐下沉，每一趟都会有一个“最大”的石块沉到水底。 17 17236。 93 14173598 95 9A 初始关 第 第 第 第 第 冒泡排序后 越置泡排序后 泡排序后 第四雪泡排序后 第五冒泡排序后 雪泡排序后 雪泡排序后 八雪泡排序后 图9.5冒泡排序示例 9.4.4快速排序 快速排序是冒泡排序的一种改进算法， 于快速排序算法元素之间的比较次数较少，速度较快，因而得名快速 排序。在各种内部排序算法中，快速排序被认为是目前最好的一种排序方法。 它的基本思想是：在初始数字序列中，任意选取一个元素（通常选择第一个数字元素）作为基准元素，也被成 为枢轴。把小于等于基准元素的所有元素都移动到基准元素的前面，把大于基准元素的所有元素都移动到基准元素 的后面。这样，基准元素所处的位置恰恰就是排序的最终位置，同时它把整个序列划分为前后两个子序列。其中前 面的子序列中 元素都 于等于基准元素，后面的 子序列中的元素都大于基准元素。 样的 一个过程被称作一趟快 速排序。接下来分别对这两个子序列重复上述操作，直到所有的元素都被移动到排序后它们应该在的位置上。 对初始关键字序列51,36,67,90,74,17,23,44,9,82}进行快速排序.首先选取第一个数字作为枢轴，也就是数字51， 它的位置是1，我们用变量i米保存这个位置，即i1.再设置一个变量j来记录最后一个数字82的位置，也就是j10。 如图9.6所示。 初始元素：{51,36,67,90,74,17,23,44,9,82 个=1 个=10

9.4.3 冒泡法排序 冒泡排序法的思想比较简单，对于 n 个元素，从第一个开始依次比较相邻的两个，如果是逆序就交换它们的位 置。重复多次以后，最大（或最小）的元素就“沉到”列表的最后一个位置。第二遍操作将第二大（或小）的元素 沉下去，这样一直操作，直到 n-1 遍后，列表就排好序了。我们以 10 个数字的升序排列为例讲解这个算法。 算法分析： 首先将第 1 个数字和第 2 个数字进行比较，若为逆序（即第 1 个数字大于第 2 个数字），则交换两个变量的值。 然后比较第 2 个数字和第 3 个数字的值，若为逆序则交换之。依次类推，直到第 9 个和第 10 个数字比较完为止。 这个过程称为第一趟冒泡排序，其结果是将最大的数字转移到最后一个位置上。然后进行第二趟冒泡排序，对前 9 个数字进行同样操作，将第二大的数字转移到第九个数字的位置。这样的冒泡排序一共需要进行 9 趟。由此得到算 法 9.5。图 9.3 展示了冒泡排序的一个实例，从图中可以看出，在冒泡排序的过程中，小的数字好比水中的气泡逐渐 向上漂浮，大的数字就像石块一样逐渐下沉，每一趟都会有一个“最大”的石块沉到水底。 图 9.5 冒泡排序示例 9.4.4 快速排序 快速排序是冒泡排序的一种改进算法，由于快速排序算法元素之间的比较次数较少，速度较快，因而得名快速 排序。在各种内部排序算法中，快速排序被认为是目前最好的一种排序方法。 它的基本思想是：在初始数字序列中，任意选取一个元素（通常选择第一个数字元素）作为基准元素，也被成 为枢轴。把小于等于基准元素的所有元素都移动到基准元素的前面，把大于基准元素的所有元素都移动到基准元素 的后面。这样，基准元素所处的位置恰恰就是排序的最终位置，同时它把整个序列划分为前后两个子序列。其中前 面的子序列中的元素都小于等于基准元素，后面的子序列中的元素都大于基准元素。这样的一个过程被称作一趟快 速排序。接下来分别对这两个子序列重复上述操作，直到所有的元素都被移动到排序后它们应该在的位置上。 对初始关键字序列{51,36,67,90,74,17,23,44,9,82}进行快速排序。首先选取第一个数字作为枢轴，也就是数字 51， 它的位置是 1，我们用变量 i 来保存这个位置，即 i=1。再设置一个变量 j 来记录最后一个数字 82 的位置，也就是 j=10。 如图 9.6 所示

图9.6序列初始状态 第一趟快速排序的操作步骤如下： ,直到i指向的元素大于等于基准元素51，或者i指向序列的尾部，即10为止。然 后反宴行1的族作，直到]指向的元素小于装雅元素5，或者指向序列的首部，即1为止，执行完这步据 作的序列状态如图97所示。 {51,36,67,90,74,17,23,449.82} 个=3 个=9 图9.7步骤1)完成后的序列状态 (2)若此时1K,则将1和j指向的元素互换，如图9.8所示。 {5136,9,90,74,17,23,44,67,82} 个3 个9 图9.8实现第一次交换 现在完成了第一次互换，然后重复执行步骤(1)和步骤(2)。直到≥1为止，再执行步骤3)。具体执行步骤如下： 反复执行+1，直到i指向的元素大于等于基准元素51，然后反复执行1，直到j指向的元素小于基准元素 51,这时的序列状态如图9.9a)所示。 {51,36,9,90,74,17,23,44.67,82}{51,36,9,44,74,17,23,90,67,82 个=4 个j=8 个=4 个=8 (b) 此时，将1和指向的元素互换，互换后的结果如图9.9b)所示。继续重复执行步(2之后1和j的位置如 图9.9c)所示。然后将i和j指向的元素的位置互换，结果如图9.9所示 {51,36,9,44,74,17,23,90,67,82}{51,36,9,44,23,17,74,90,67,82 个5个7 个=5个=7 图9.9快速排序分解步骤 继续执行+1，直到i指向的元素大于等于基准元素51，继续执行j1,直到j指向的元素小于基准元素51， 执行完之后1和1的位置如图9.10所示，步骤(2执行完毕。 {51,36,9,44,23,17,74,90,67,82} i=6个个ie7 图9.10步骤(2)执行完毕的序列状态 3)此时≥j,将基准元素51与j指向的元素交换位置，如图9.11所示。 {17,36,9,44,23,51,74,90,67,821 j6个个7 图9.11完成原序列的第一次划分 至此完成了原序列的第一次划分，基准元素51移动到了排序后的最终位置上，它的前半序列都小于51，后半 序列都大于51。如下所示： {17,36,9,44,23b51,{74,90,67,82} 接下来分别对基准元素51前后的子序列中长度大于1的子序列重复上述操作，直到整个序列排列有序。我们 以51前面的子序列为例，它的基准元素是17，排序过程如下。 《11736.9,44,23151,{74,90,67,82} 1的初始位置是1，j的初始位置是5，反复执行=+1，直到i指向的元素大于等于基准元素17。继续执行j-1

图 9.6 序列初始状态 第一趟快速排序的操作步骤如下： (1)反复执行 i=i+1 的操作，直到 i 指向的元素大于等于基准元素 51，或者 i 指向序列的尾部，即 i=10 为止。然 后反复执行 j=j-1 的操作，直到 j 指向的元素小于基准元素 51，或者 j 指向序列的首部，即 j=1 为止。执行完这步操 作的序列状态如图 9.7 所示。 图 9.7 步骤(1)完成后的序列状态 (2)若此时 i<j，则将 i 和 j 指向的元素互换，如图 9.8 所示。 图 9.8 实现第一次交换 现在完成了第一次互换，然后重复执行步骤(1)和步骤(2)，直到 i≥j 为止，再执行步骤(3)。具体执行步骤如下： 反复执行 i=i+1，直到 i 指向的元素大于等于基准元素 51，然后反复执行 j=j-1，直到 j 指向的元素小于基准元素 51，这时的序列状态如图 9.9(a)所示。 (a) (b) 此时，将 i 和 j 指向的元素互换，互换后的结果如图 9.9(b)所示。继续重复执行步骤(1)、(2)之后 i 和 j 的位置如 图 9.9(c)所示。然后将 i 和 j 指向的元素的位置互换，结果如图 9.9(d)所示。 (c) (d) 图 9.9 快速排序分解步骤 继续执行 i=i+1，直到 i 指向的元素大于等于基准元素 51，继续执行 j=j-1，直到 j 指向的元素小于基准元素 51， 执行完之后 i 和 j 的位置如图 9.10 所示，步骤(2)执行完毕。 图 9.10 步骤(2)执行完毕的序列状态 (3)此时 i≥j，将基准元素 51 与 j 指向的元素交换位置，如图 9.11 所示。 图 9.11 完成原序列的第一次划分 至此完成了原序列的第一次划分，基准元素 51 移动到了排序后的最终位置上，它的前半序列都小于 51，后半 序列都大于 51。如下所示： { { 17, 36, 9, 44, 23 }, 51, { 74, 90, 67, 82 } } 接下来分别对基准元素 51 前后的子序列中长度大于 1 的子序列重复上述操作，直到整个序列排列有序。我们 以 51 前面的子序列为例，它的基准元素是 17，排序过程如下： { { 17, 36, 9, 44, 23 }, 51, { 74, 90, 67, 82 } } i 的初始位置是 1，j 的初始位置是 5，反复执行 i=i+1，直到 i 指向的元素大于等于基准元素 17。继续执行 j=j-1