山东理工大学：《计算机算法设计与分析》课程教学课件（PPT讲稿）哈夫曼编码 Huffman Coding

白东程子太军 计算机算法设计与分析 Design and Analysis of Computer Algorithms 哈夹曼隔码 Huffman Coding 我浩 信科1801

计算机算法设计与分析 Design and Analysis of Computer Algorithms 哈夫曼编码 Huffman Coding 张浩 信科1801

归本程子末军 目录 SHANDONG UNIVERSITY OF TECHNOLOOY 一、 编码问题的提出 二、可变长编码和前缀编码 三、哈夫曼树和哈夫曼编码 四、哈夫曼编码算法实现（树结构) 五、哈夫曼编码算法实现（广义表) 2025/4/3 2

2 目录 一、编码问题的提出 二、可变长编码和前缀编码 三、哈夫曼树和哈夫曼编码 四、哈夫曼编码算法实现（树结构） 五、哈夫曼编码算法实现（广义表） 2025/4/3

归本程上太军 1.编码问题的提出 SHANDONG UNIVERSITY OF TECINOLOGY 在英文中已知e的出现频率最高，z的出现频率 最低。在信息加密之前需要对信息进行编码处理， 而编码后的二进制数据长度将直接影响加密速度。 如果每个字母都采用等 长编码的方式进行编码势 必会多占用很多空间。所 以我们很容易思考到，有 没有一种可变长的编码既 可以减少编码长度又可以 David Huffman 唯一的恢复出来？ 2025/4/3 3

3 1.编码问题的提出 在英文中已知e的出现频率最高，z的出现频率 最低。在信息加密之前需要对信息进行编码处理， 而编码后的二进制数据长度将直接影响加密速度。 2025/4/3 如果每个字母都采用等 长编码的方式进行编码势 必会多占用很多空间。所 以我们很容易思考到，有 没有一种可变长的编码既 可以减少编码长度又可以 David Huffman 唯一的恢复出来？

归本程子末军 2.可变长编码和前缀编码 HANDONG UNIVERSITY OF TECHNOLOOY 如果采用可变长编码进行对信息进行编码，最 直接的方法就是直接采用“0,1,01,10.”的方式 进行编码。这种编码方式真的合适吗？ 例：我们对A,B,C,D四个字母进行编码。我们 采用的编码方式如下： A B C D 0 01 10 请问：“0110”到底是的原信息到底是“ABBA” 还是“ABD”或者是“CD”呢？ 2025/4/3

4 2.可变长编码和前缀编码 如果采用可变长编码进行对信息进行编码，最 直接的方法就是直接采用“0,1,01,10.”的方式 进行编码。这种编码方式真的合适吗？ 2025/4/3 例：我们对A,B,C,D四个字母进行编码。我们 采用的编码方式如下： A B C D 0 1 01 10 请问：“0110”到底是的原信息到底是“ABBA” 还是“ABD”或者是“CD”呢？

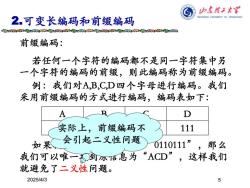
归本程上太军 2.可变长编码和前缀编码 SHANDONG UNIVERSITY OF TECINOLOGY 前缀编码： 若任何一个字符的编码都不是同一字符集中另 一个字符的编码的前缀，则此编码称为前缀编码。 例：我们对A,B,C,D四个字母进行编码。我们 采用前缀编码的方式进行编码，编码表如下： A 实际上，前缀编码不 111 如果 会引起二义性问题 0110111”,那么 我们可以唯一到际后息为“ACD”，这样我们 就避免了二义性问题。 2025/413 5

5 2.可变长编码和前缀编码 前缀编码： 若任何一个字符的编码都不是同一字符集中另 一个字符的编码的前缀，则此编码称为前缀编码。 2025/4/3 例：我们对A,B,C,D四个字母进行编码。我们 采用前缀编码的方式进行编码，编码表如下： A B C D 0 10 110 111 如果我们给定编码信息为“0110111” ，那么 我们可以唯一找到原信息为“ACD” ，这样我们 就避免了二义性问题。 实际上，前缀编码不 会引起二义性问题

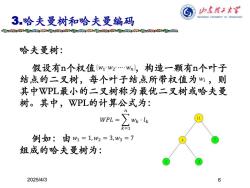
归本程子末军 3.哈夫曼树和哈夫曼编码 HANDONG UNIVERSITY OF TECINOLOGY 哈夫曼树： 假设有n个权值{w1w2w,构造一颗有n个叶子 结，点的二叉树，每个叶子结点所带权值为“，则 其中WL最小的二叉树称为最优二叉树或哈夫曼 树。其中，WPL的计算公式为： wPL=∑wklk 例如：由w1=1,w2=3,w3=7 组成的哈夫曼树为： 2025/413

6 3.哈夫曼树和哈夫曼编码 2025/4/3 哈夫曼树： 假设有n个权值 ，构造一颗有n个叶子 结点的二叉树，每个叶子结点所带权值为 ，则 其中WPL最小的二叉树称为最优二叉树或哈夫曼 树。其中，WPL的计算公式为： 𝑊𝑃𝐿 = ෍ 𝑘=1 𝑛 𝑤𝑘 ⋅ 𝑙𝑘 𝑤1 𝑤2 ⋯ 𝑤𝑛 𝑤𝑖 例如：由 组成的哈夫曼树为： 𝑤1 = 1, 𝑤2 = 3, 𝑤3 = 7

归本程上太军 3.哈夫曼树和哈夫曼编码 SHANDONG UNIVERSITY OF TECINOLOGY 如何构造哈夫曼树： 1,根据给定的n个权值W'WzWn},构造包含n颗 二叉树的集合F={阳2Tn,其中每颗二叉树中均只 含一个带权值为的根结点，其左、右子树为空树； 2，在F中选取其根结，点的权值最小的两颗二叉树， 分别作为左、右子树构造一个新的二叉树，并置这 颗新的二叉树根节点的权值为其左、右子树根结点 的权值之和； 3,从F中删去这两颗树，同时加入刚生成的新树； 4,重复2和3两步，直至F中只含一颗树为止。 2025/413

7 3.哈夫曼树和哈夫曼编码 如何构造哈夫曼树： 1，根据给定的n个权值 ，构造包含n颗 二叉树的集合 ，其中每颗二叉树中均只 含一个带权值为 的根结点，其左、右子树为空树； 2，在F中选取其根结点的权值最小的两颗二叉树， 分别作为左、右子树构造一个新的二叉树，并置这 颗新的二叉树根节点的权值为其左、右子树根结点 的权值之和； 3，从F中删去这两颗树，同时加入刚生成的新树； 4，重复2和3两步，直至F中只含一颗树为止。 2025/4/3 𝑤1 𝑤2 ⋯ 𝑤𝑛 F = 𝑇1 𝑇2 ⋯ 𝑇𝑛 𝑤𝑖

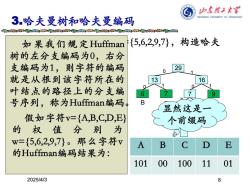
归东程子太军 HANDONG UNIVERSITY OF TECHNOLOOY 3.哈夫曼树和哈夫曼编码 如果我们规定Iuffman {5,6,2,9,7},构造哈夫 树的左分支编码为0，右分 支编码为1，则字符的编码 0 就是从根到该字符所在的 13 16 叶结点的路径上的分支编 9 号序列，称为Iuffman编码 d 显然这是一 假如字符v={A,B,C,D,E} 个前缀码 的权值分别为 w={5,6,2,9,7}。那么字符v A B E 的Huffman编码结果为： 101 00 100 11 01 2025/413

8 3.哈夫曼树和哈夫曼编码 例：已知权值的集合W={5,6,2,9,7}，构造哈夫 曼树。 2025/4/3 5 6 2 9 7 6 9 7 7 2 5 9 13 7 6 7 2 5 7 9 13 7 2 5 6 16 7 9 13 7 2 5 6 16 29 0 0 0 0 1 1 1 1 如 果我 们规定 Huffman 树的左分支编码为0，右分 支编码为1，则字符的编码 就是从根到该字符所在的 叶结点的路径上的分支编 号序列，称为Huffman编码。 假如字符v={A,B,C,D,E} 的 权 值 分 别 为 w={5,6,2,9,7}。那么字符v 的Huffman编码结果为： A B C D E 101 00 100 11 01 E D C B A 显然这是一 个前缀码

归东程子末军 4哈夫曼编码算法实现（树结构) SHANDONG UNIVERSITY OF TECINOLOGY 由于哈夫曼树中没有度为1的结点，所以，一 颗有n个叶子结点的哈夫曼树共有2n-1个结点，可 以存储在一个大小为2n-1的一维数组中。=n2+1 设哈夫曼树的存储表示为： Typedef struct{ unsigned int weight; unsigned int parent,lchild,rchild; }HTNode,.*Huffman Tree;∥动态分配数组存储哈夫曼树 Typedef char*HuffmanCode,〃动态分配数组存储哈夫曼编码表 2025/413

9 4.哈夫曼编码算法实现（树结构） 由于哈夫曼树中没有度为1的结点，所以， 一 颗有n个叶子结点的哈夫曼树共有2n-1个结点，可 以存储在一个大小为2n-1的一维数组中。 2025/4/3 设哈夫曼树的存储表示为： Typedef struct{ unsigned int weight; unsigned int parent, lchild, rchild; }HTNode, *Huffman Tree; //动态分配数组存储哈夫曼树 Typedef char *HuffmanCode; //动态分配数组存储哈夫曼编码表

白东程子太军 4.哈夫曼编码算法实现（树结构) HANDONG UNIVERSITY OF TECHNOLOGY 器会清修会合条会的点不空.华合会的是条 w存放n个字符的权值，构造哈夫曼树HT,并求出n个字符的哈夫曼编码HC。 Void HuffmanCoding(HuffmanTree &HT,HuffmanCode &HC,int *w,int n){ if(n<=1)return; m=2*n-1; ∥初始化存储结构； for(i=n+1;i<=m;+i){/∥建哈夫曼树 ∥在HT1.i-1]选择parent:为0且权值最小的两个结点，其序号分别为s1,s2. Select(HT,i-1,s1,s2);∥第i个结，点就是第i-1个和第i-2个结，点的双亲结，点。 HT[s1].parent=i; HT[s2].parent=i; HT[i].Ichild=s1; HT[i].rchild=s2; 建哈夫曼树 HT[i].weight=HT[s1].weight+HT[s2].weight; 算法 2025/4/3 10

10 4.哈夫曼编码算法实现（树结构） //w存放n个字符的权值，构造哈夫曼树HT，并求出n个字符的哈夫曼编码HC。 Void HuffmanCoding(HuffmanTree &HT, HuffmanCode &HC, int *w, int n){ if(n <= 1) return; m = 2*n-1; //初始化存储结构； for(i = n+1; i <= m; ++i){ //建哈夫曼树 //在HT[1.i-1]选择parent为0且权值最小的两个结点，其序号分别为s1,s2. Select(HT, i-1,s1, s2); //第i个结点就是第i-1个和第i-2个结点的双亲结点。 HT[s1].parent = i; HT[s2].parent = i; HT[i].lchild = s1; HT[i].rchild = s2; HT[i].weight = HT[s1].weight + HT[s2].weight; } 2025/4/3 建哈夫曼树 算法