《数据结构与算法分析》课程教学资源（书籍文献）数据结构与算法分析

第1章绪论 1.1数据结构的地位 12基本概念和术语 1.2.1关于数据结构的几个基本概念 1.22数据结构的种类。 3 1.23数据结构的形式化定义 1.24数据的物理结构 1.2.5抽象数据类型ADT 5 1.3数学预备知识 6 1.3.1集合 .6 1.32常用的数学术语 .6 133对数 、> 1.4算法和算法分析 1.4.1算法 7 1.4.2算法设计的要求 1.43算法时间效率的度量. 1.4.3算法的空间复杂度(space complexity) 14 第2音线性表 2.1线性表的类型定义 15 2.2线性表的顺序存储和基本操作的实现 .17 2.2.1顺序存储 17 2.22顺序存储结构下基本操作分析 18 2.2.3源码实现 22.4顺序表应用举例 2.3线性表的链式表示和实现 3 2.3.1基本术语 3 2.3.2链式存储结构下基本操作分析 34 .56 31相 56 3.11基本概念。 56 3.12抽象数据类型栈的定义 3.2栈的顺序存储. 58 321栈的顺序存储定义 3.22基本操作分析 59 323源玛实现 60 33钱的链式存储 63 3.4栈的应用举例 3.4.1数制转换 67

1 第 1 章 绪论.1 1.1 数据结构的地位.1 1.2 基本概念和术语.2 1.2.1 关于数据结构的几个基本概念. 2 1.2.2 数据结构的种类.2 1.2.3 数据结构的形式化定义. 3 1.2.4 数据的物理结构.4 1.2.5 抽象数据类型 ADT. 5 1.3 数学预备知识.6 1.3.1 集合.6 1.3.2 常用的数学术语.6 1.3.3 对数.7 1.4 算法和算法分析.7 1.4.1 算法.7 1.4.2 算法设计的要求. 10 1.4.3 算法时间效率的度量.11 1.4.3 算法的空间复杂度（space complexity）. 14 第 2 章 线性表.15 2.1 线性表的类型定义. 15 2.2 线性表的顺序存储和基本操作的实现. 17 2.2.1 顺序存储.17 2.2.2 顺序存储结构下基本操作分析. 18 2.2.3 源码实现.20 2.2.4 顺序表应用举例. 29 2.3 线性表的链式表示和实现. 31 2.3.1 基本术语.31 2.3.2 链式存储结构下基本操作分析. 34 2.4 一元多项式的表示和相加. 52 第 3 章 栈和队列.56 3.1 栈.56 3.1.1 基本概念：.56 3.1.2 抽象数据类型栈的定义. 57 3.2 栈的顺序存储.58 3.2.1 栈的顺序存储定义. 58 3.2.2 基本操作分析.59 3.2.3 源码实现.60 3.3 栈的链式存储.63 3.4 栈的应用举例.67 3.4.1 数制转换.67

3.4.2表达式求值 68 3.5队列 71 3.51基本概念 .71 352抽象数据类型队列的定义 72 3.5.3队列的链式存储和实现 73 3.3.4队列的顺序存储和实现 80 3.4队列的应用。 "8o 第四章串 91 4.1串类型的定义 .92 411基本概念 .92 412由的存储方式 92 4.1.3顺序存储结构下基本操作的实现 .93 4.14JAVA语言中的字符串类型 98 第五章数组和广义表 10 51粉斯组 101 5.2数组的存储. .101 53矩阵 104 5.3.1特殊矩阵的压缩存储 104 5.4义表 122 54.1广义表的定义 122 5.42广义表的存储结构 124 5.5m元多项式的表示 126 5.6求广义表深度基本操作的实现 127 第六章树和二叉树」 132 6.1树的定义和基本术语 132 6.1.1树的定义 132 612树的基本术语 133 6.13树的表示形式 134 6.14抽象数据类型树的定义. .134 6,2二叉树(Binary Tree)) 135 621二叉树的定义 135 6.2.2二叉树的性质」 137 623二叉树的存储结构 142 6.3遍历二叉树(Traversing Binary Tree)和线索二叉树 150 6.3.1遍历二叉树(Traversing Binary Tree). 150 6.3.2二叉线索链表 155 64树和森林 ,161 6.4.1树的存储 161 6.42森林与二叉树的转换 166

2 3.4.2 表达式求值.68 3.5 队列.71 3.5.1 基本概念.71 3.5.2 抽象数据类型队列的定义. 72 3.5.3 队列的链式存储和实现. 73 3.3.4 队列的顺序存储和实现. 80 3.4 队列的应用.89 第四章 串.91 4.1 串类型的定义.92 4.1.1 基本概念.92 4.1.2 串的存储方式.92 4.1.3 顺序存储结构下基本操作的实现. 93 4.1.4 JAVA 语言中的字符串类型. 98 第五章 数组和广义表. 101 5.1 数组.101 5.2 数组的存储.101 5.3 矩阵.104 5.3.1 特殊矩阵的压缩存储. 104 5.4 广义表.122 5.4.1 广义表的定义.122 5.4.2 广义表的存储结构. 124 5. 5 m 元多项式的表示. 126 5.6 求广义表深度基本操作的实现. 127 第六章 树和二叉树.132 6.1 树的定义和基本术语. 132 6.1.1 树的定义.132 6.1.2 树的基本术语.133 6.1.3 树的表示形式.134 6.1.4 抽象数据类型树的定义. 134 6.2 二叉树 (Binary Tree).135 6.2.1 二叉树的定义.135 6.2.2 二叉树的性质.137 6.2.3 二叉树的存储结构. 142 6.3 遍历二叉树 (Traversing Binary Tree) 和线索二叉树. 150 6.3.1 遍历二叉树 (Traversing Binary Tree). 150 6.3.2 二叉线索链表.155 6.4 树和森林.161 6.4.1 树的存储.161 6.4.2 森林与二叉树的转换. 166

6.43树与森林的骗历 169 6.5树与等价问题. 170 6.6赫夫曼树(Huffman Tree)及其应用. 178 6.6.1路径长度(Path Length) 178 6.6.2带权路径长度(Weighted Path Length,WPL). .178 6.6.3 Huffman(哈夫曼)树 179 6.6.4赫夫曼树的应用. 179 665顶码实现 184 6.7回溯法与树的遍历. 190 68树的计数 193 第七章图 错误！未定义书签。 7.1图的定义和术语 错操！未定义书签 72图的存储结构. 错误！未定义书签。 7.2.1邻接矩阵(adjacency matrix) 错误】未定义书签 7.2.2邻接表(adjacency 错误！未定义书签 7.2.3邻接多重表 错误！未定义书签 7.2.4十字链表 错误！未定义书签。 7.3图的遍历. 错误！未定义书签。 7.3.1深度优先遍历 错误！未定义书签 7.3.2广度优先遍历. 错误！未定义书签。 7.4图的连通性问题 错误1 未定义书签 7.4.1无向图的连通分量和生成树 错误！未定义书签 7.42有向图的强连通分量 错误！未定义书签 7.4.3最小生成树Minimum Spanning Cost Tree). 错误！未定义书签。 7,4.4关节点和重连通分量 错误！未定义书签 7.5有向无环图及其应用 错误未定义书签。 7.5.1拓扑排序」 错误！未定义书签 7.52关键路径 错误！未定义书签 7.6最短路径 错误！未定义书签 7.6.】某一顶点到其余各点最短路径 错误未定义书签。 7.6.2每一对顶点之间的最短路径 错误！未定义书签 第8章查找 错误！未定义书签 8.1查找的概念 错误未定义书签。 8.2静态查找。 错误！未定义书签 821顺序查找 错误！未定义书签。 8.2.2折半查找(Binary Search). 错误！未定义书签。 823分块杳找 错误」未定义书答 8.3动态查找 错误！未定义书签 8.3.1二叉排序树(BST)的定义. 错误！未定义书签

3 6.4.3 树与森林的遍历. 169 6.5 树与等价问题.170 6.6 赫夫曼树 (Huffman Tree)及其应用. 178 6.6.1 路径长度 (Path Length). 178 6.6.2 带权路径长度 ( Weighted Path Length, WPL ).178 6.6.3 Huffman(哈夫曼)树. 179 6.6.4 赫夫曼树的应用. 179 6.6.5 源码实现.184 6.7 回溯法与树的遍历. 190 6.8 树的计数.193 第七章 图. 错误！未定义书签。 7.1 图的定义和术语. 错误！未定义书签。 7.2 图的存储结构. 错误！未定义书签。 7.2.1 邻接矩阵（ adjacency matrix）.错误！未定义书签。 7.2.2 邻接表（adjacency list）. 错误！未定义书签。 7.2.3 邻接多重表. 错误！未定义书签。 7.2.4 十字链表. 错误！未定义书签。 7.3 图的遍历. 错误！未定义书签。 7.3.1 深度优先遍历. 错误！未定义书签。 7.3.2 广度优先遍历. 错误！未定义书签。 7.4 图的连通性问题. 错误！未定义书签。 7.4.1 无向图的连通分量和生成树.错误！未定义书签。 7.4.2 有向图的强连通分量.错误！未定义书签。 7.4.3 最小生成树(Minimum Spanning Cost Tree).错误！未定义书签。 7.4.4 关节点和重连通分量.错误！未定义书签。 7.5 有向无环图及其应用.错误！未定义书签。 7.5.1 拓扑排序. 错误！未定义书签。 7.5.2 关键路径. 错误！未定义书签。 7.6 最短路径. 错误！未定义书签。 7.6.1 某一顶点到其余各点最短路径.错误！未定义书签。 7.6.2 每一对顶点之间的最短路径.错误！未定义书签。 第 8 章 查找. 错误！未定义书签。 8.1 查找的概念. 错误！未定义书签。 8.2 静态查找. 错误！未定义书签。 8.2.1 顺序查找. 错误！未定义书签。 8.2.2 折半查找(Binary Search).错误！未定义书签。 8.2.3 分块查找. 错误！未定义书签。 8.3 动态查找. 错误！未定义书签。 8.3.1 二叉排序树(BST)的定义.错误！未定义书签

8.3.2BST树的查找 错误！未定义书签 83.3BST树的插入 错误！未定义书签。 8.34BST树的删除 错误！未定义书签 8.3.5BST树的查找分析 错误！未定义书签 8.4平衡二叉树(AVL). 错误！未定义书签 8.4.1平衡二叉树的定义 错误！未定义书签 8.4.2平衡化旋转 错误！未定义书签 8.4.3平衡二叉排序树的插入 错误！未定义书签 8.4.4平衡二叉排序树构造实例 错误！未定义书签 8.45平衡二叉树查找分析 错误！未定义书签 85索引杳战 错误！未定义书签。 8.5.1顺序索引表 错误！未定义书签。 852树形索表 错误！未定义书签 8.6哈希（散列）查找， 错误！未定义书签。 861基本概今 错误】未定义书答 8.6.2哈希函数的构造 错误1未定义书签。 863冲突处理的方法 错误」未定义书答 8.6.4哈希查找过程及分析 错误！未定义书签 第9章内部排序 错误】未定义书签 9.1排序的基本概念 错误！未定义书签 9.2插入排序 错误！未定义书签 9.2.1直接插入排序 错误！未定义书签。 9.2.2其它插入排序 错误！未定义书签 9.23希尔排序 错误！未定义书签 9.3快速排序 错误！未定义书签 9.3.1冒泡排序 错误！未定义书签 9.3.2快速排序。 错误！未定义书签 9.4选择排序 错误！未定义书签 9.4.1简单选择排序 错误！未定义书签 9.4.2树形选择排序 错误！ 未定义书签 9.4.3堆排序. 错误！未定义书签 9.5归并排序 错误！未定义书签 96其数排序 错误！未定义书签。 9.6.1多关键字排序 错误！未定义书签。 9.6.2链式基数排序 错误！未定义书签。 9.7各种内部排序的比较 错误！未定义书签 第10章文件 错误！未定义书签 10.1文件的概念 错误！未定义书签。 10.2顺序文件 错误！未定义书签

4 8.3.2 BST 树的查找.错误！未定义书签。 8.3.3 BST 树的插入.错误！未定义书签。 8.3.4 BST 树的删除.错误！未定义书签。 8.3.5 BST 树的查找分析.错误！未定义书签。 8.4 平衡二叉树(AVL).错误！未定义书签。 8.4.1 平衡二叉树的定义.错误！未定义书签。 8.4.2 平衡化旋转. 错误！未定义书签。 8.4.3 平衡二叉排序树的插入.错误！未定义书签。 8.4.4 平衡二叉排序树构造实例.错误！未定义书签。 8.4.5 平衡二叉树查找分析.错误！未定义书签。 8. 5 索引查找. 错误！未定义书签。 8.5.1 顺序索引表. 错误！未定义书签。 8.5.2 树形索引表. 错误！未定义书签。 8. 6 哈希(散列)查找.错误！未定义书签。 8.6.1 基本概念. 错误！未定义书签。 8.6.2 哈希函数的构造.错误！未定义书签。 8.6.3 冲突处理的方法.错误！未定义书签。 8.6.4 哈希查找过程及分析.错误！未定义书签。 第 9 章 内部排序. 错误！未定义书签。 9.1 排序的基本概念. 错误！未定义书签。 9.2 插入排序. 错误！未定义书签。 9.2.1 直接插入排序. 错误！未定义书签。 9.2.2 其它插入排序. 错误！未定义书签。 9.2.3 希尔排序. 错误！未定义书签。 9.3 快速排序. 错误！未定义书签。 9.3.1 冒泡排序. 错误！未定义书签。 9.3.2 快速排序. 错误！未定义书签。 9. 4 选择排序. 错误！未定义书签。 9.4.1 简单选择排序. 错误！未定义书签。 9.4.2 树形选择排序. 错误！未定义书签。 9.4.3 堆排序. 错误！未定义书签。 9. 5 归并排序. 错误！未定义书签。 9. 6 基数排序. 错误！未定义书签。 9.6.1 多关键字排序. 错误！未定义书签。 9.6.2 链式基数排序. 错误！未定义书签。 9.7 各种内部排序的比较.错误！未定义书签。 第 10 章 文件. 错误！未定义书签。 10. 1 文件的概念. 错误！未定义书签。 10. 2 顺序文件. 错误！未定义书签

10.3索引文件， 错误1未定义书签 10.4ISAM文件 错误！未定义书签 10.5VSAM文件. 错误！未定义书签。 10.6直接存取文件 错误未定义书签。 10.7多关键字文件 错误！未定义书签。 10.7.1多重表文件 错误！未定义书签。 10.7.2倒排文件. 错误！未定义书签 10.8外部排序 错误！未定义书签 10.8.1外部排序方法 错误！未定义书签。 10.8.2外排序的时间分析 错误1未定义书签

5 10. 3 索引文件. 错误！未定义书签。 10. 4 ISAM 文件. 错误！未定义书签。 10.5 VSAM 文件.错误！未定义书签。 10. 6 直接存取文件. 错误！未定义书签。 10. 7 多关键字文件. 错误！未定义书签。 10. 7.1 多重表文件. 错误！未定义书签。 10.7.2 倒排文件. 错误！未定义书签。 10.8 外部排序. 错误！未定义书签。 10.8.1 外部排序方法. 错误！未定义书签。 10.8.2 外排序的时间分析.错误！未定义书签

第1章绪论 1.1数据结构的地位 计算机诞生之初用于科学计算，现在主要用于数据处理。数据处理就是对现实世界中的 原始数据进行处理，最后得到人们所需的数据。但是由于很多原始数据是杂乱无章的，首先 得把它转化成有组织的数据，然后在这个有组织的数据的基础之上编写算法，得到人们所需 的数据。通俗地说，怎样把原始数据转化成有组织的数据，就是数据结构这门课的研究内容： 单有算法构成不了程序，只有加上数据结构之后，它才成为程序。不会数据结构，就不会编 写出程序。数据结构的地位如图1-1所示 原始数据 所需数据 原始数据 有组织的数据 一所需数据 数据结构 程 图1一1数据结构的地位 我们知道，虽然每个人都懂得英语的语法与基本类型，但是对于同样的题目，每个人写 出的作文，水平却高低不一。程序设计也和写英语作文一样，虽然程序员都懂得语言的语法 与语义，但是对于同样的问题，程序员写出来的程序不一样。有的人写出来的程序效率很高， 有的人却用复杂的方法来解决一个简单的问题。当然，程序设计水平的提高仅仅靠看几本程 序设计书是不行的。只有多思索、多练习，才能提高自己的程序设计水平：否则，书看得再 多，提高也不大。记得刚学程序设计时，常听人说程序设计水平要想提高，最重要的是多看 别人写的程序，多去思考问题。从别人写的程序中，我们可以发现效率更高的解决方法：从 思考问题的过程中，我们可以了解解决问题的方法常常不只一个。运用先前解决问题的经验， 来解决更复杂更深入的问题，是提高程序设计水平的最有效途径。数据结构正是前人在思索 问题的过程中所想出的解决方法。一般而言，在学习程字设计一段时间后，学习"数据结构" 便能让你的程序设计水平上一个台阶。如果只学会了程序设计的语法和语义，那么你只能解 决程序设计三分之一的问题，而且运用的方法并不是最有效的。但如果学会了数据结构的概 念，就能在程序设计上，运用最有效的方法来解决绝大多数的问题

1 第 1 章 绪论 1.1 数据结构的地位 计算机诞生之初用于科学计算，现在主要用于数据处理。数据处理就是对现实世界中的 原始数据进行处理，最后得到人们所需的数据。但是由于很多原始数据是杂乱无章的，首先 得把它转化成有组织的数据，然后在这个有组织的数据的基础之上编写算法，得到人们所需 的数据。通俗地说，怎样把原始数据转化成有组织的数据，就是数据结构这门课的研究内容； 单有算法构成不了程序，只有加上数据结构之后，它才成为程序。不会数据结构，就不会编 写出程序。数据结构的地位如图 1-1 所示： 图 1－1 数据结构的地位 我们知道，虽然每个人都懂得英语的语法与基本类型，但是对于同样的题目，每个人写 出的作文，水平却高低不一。程序设计也和写英语作文一样，虽然程序员都懂得语言的语法 与语义，但是对于同样的问题，程序员写出来的程序不一样。有的人写出来的程序效率很高， 有的人却用复杂的方法来解决一个简单的问题。当然，程序设计水平的提高仅仅靠看几本程 序设计书是不行的。只有多思索、多练习，才能提高自己的程序设计水平；否则，书看得再 多，提高也不大。记得刚学程序设计时，常听人说程序设计水平要想提高，最重要的是多看 别人写的程序，多去思考问题。从别人写的程序中，我们可以发现效率更高的解决方法；从 思考问题的过程中，我们可以了解解决问题的方法常常不只一个。运用先前解决问题的经验， 来解决更复杂更深入的问题，是提高程序设计水平的最有效途径。数据结构正是前人在思索 问题的过程中所想出的解决方法。一般而言，在学习程序设计一段时间后，学习"数据结构" 便能让你的程序设计水平上一个台阶。如果只学会了程序设计的语法和语义，那么你只能解 决程序设计三分之一的问题，而且运用的方法并不是最有效的。但如果学会了数据结构的概 念，就能在程序设计上，运用最有效的方法来解决绝大多数的问题

1.2基本概念和术语 1.2.1关于数据结构的几个基本概念 1.数据(daa):是对客观事物的符号表示，所有能输入到计算机中，被计算机程序识别 和处理的符号的总称。计算机程序处理各种各样的数据，可以是数值数据，如整数、 实数或复数：也可以是非数值数据，如字符、文字、图形、图像、声音等 2.数据元素(data element):数据结构的基本组成单位。数据结构研究的就是数据 元素以及数据元素之间的关系。一个数据元素可由一个或若干个数据项组成。 例如：描述一个学生信息的数据元素可由下列数据项组成： 姓名学号班号性别出生日期入学成绩 3数据对象Data Object)):是性质相同的数据元素的集合。 整数的数据对象是{-3，-2，-1,0,1,2,3，.} 英文字符类型的数据对象是{A,B,C,D,E,F,. 学生管理信息系统的数据对象是学校全体学生的集合 ,4数据结构（Data_Structure)相互之间存在一种或多种特定关系的数据元素的集合。 1.2.2数据结构的种类 根据数据元素之间关系的不同特性，有下列四类基本结构： 1.集合结构。在集合结构中，数据元素间的关系除了"属于同一个集合“外，别无任何 关系如图1-2所示：特别注意的是：数据元素之间有内在关系，但对于我们所研究的问题没 用，我们不去研究，我们也认为它们之间没关系。整数集合中的数据元素{3,2,1,0， 1,2,3,.除同属于一个集合外，别无任何关系。 O 图1一2集合结构 2.线性结构。该结构的数据元素之间存在着一对一的关系。每个数据元素有0个或 个前驱，0个或一个后继。如图13所示： ○

2 1.2 基本概念和术语 1.2.1 关于数据结构的几个基本概念 1.数据（data）：是对客观事物的符号表示，所有能输入到计算机中，被计算机程序识别 和处理的符号的总称。计算机程序处理各种各样的数据，可以是数值数据，如整数、 实数或复数；也可以是非数值数据，如字符、文字、图形、图像、声音等。 2.数据元素（data element）：数据结构的基本组成单位。数据结构研究的就是数据 元素以及数据元素之间的关系。一个数据元素可由一个或若干个数据项组成。 例如：描述一个学生信息的数据元素可由下列数据项组成： 姓名 学号 班号 性别 出生日期 入学成绩 3.数据对象(Data Object)：是性质相同的数据元素的集合。 整数的数据对象是{.-3，-2，-1，0，1，2，3，.} 英文字符类型的数据对象是{A，B，C，D，E，F，.} 学生管理信息系统的数据对象是学校全体学生的集合。 4.数据结构（ Data_Structure）相互之间存在一种或多种特定关系的数据元素的集合。 1.2.2 数据结构的种类 根据数据元素之间关系的不同特性，有下列四类基本结构： 1. 集合结构。在集合结构中，数据元素间的关系 除了"属于同一个集合"外，别无任何 关系,如图 1-2 所示：特别注意的是：数据元素之间有内在关系，但对于我们所研究的问题没 用，我们不去研究，我们也认为它们之间没关系。整数集合中的数据元素{.-3，-2，-1，0， 1，2，3，.}除同属于一个集合外，别无任何关系。 图 1－2 集合结构 2. 线性结构。该结构的数据元素之间存在着一对一的关系。每个数据元素有 0 个或一 个前驱，0 个或一个后继。如图 1-3 所示：

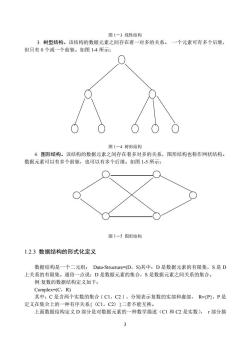
图1一3线性结构 3.树型结构。该结构的数据元素之间存在着一对多的关系。一个元素可有多个后继， 但只有0个或一个前驱。如图14所示： 图1一4树形结构 4.图形结构。该结构的数据元素之间存在着多对多的关系，图形结构也称作网状结构。 数据元素可以有多个前驱，也可以有多个后继。如图1-5所示： 图1一5图形结构 1.2.3数据结构的形式化定义 数据结构是一个二元组：Data-Structure-=(D,S)其中：D是数据元素的有限集，S是D 上关系的有限集。通俗一点说：D是数据元素的集合，S是数据元素之间关系的集合 例：复数的数据结构定义如下： Complex=(C,R) 其中：C是含两个实数的集合(C1,C2】,分别表示复数的实部和虚部，R={P;,P是 定义在集合上的一种有序关系{〈C1,C2)}二者不能互换。 上面数据结构定义D部分是对数据元素的一种数学描述(C1和C2是实数)，r部分描 3

3 图 1－3 线性结构 3. 树型结构。该结构的数据元素之间存在着一对多的关系。 一个元素可有多个后继， 但只有 0 个或一个前驱。如图 1-4 所示： 图 1－4 树形结构 4. 图形结构。该结构的数据元素之间存在着多对多的关系，图形结构也称作网状结构。 数据元素可以有多个前驱，也可以有多个后继。如图 1-5 所示： 图 1－5 图形结构 1.2.3 数据结构的形式化定义 数据结构是一个二元组： Data-Structure=(D，S)其中：D 是数据元素的有限集，S 是 D 上关系的有限集。通俗一点说：D 是数据元素的集合，S 是数据元素之间关系的集合。 例:复数的数据结构定义如下： Complex=(C，R) 其中：C 是含两个实数的集合﹛C1，C2﹜，分别表示复数的实部和虚部， R={P}，P 是 定义在集合上的一种有序关系{〈C1，C2〉}二者不能互换。 上面数据结构定义 D 部分是对数据元素的一种数学描述（C1 和 C2 是实数）， r 部分描

述的是数据元素之间的逻辑关系({(C1,C2》,是一种有序关系，C1和C2不能互换)： 并不涉及在计算机中如何表示它，把(D,S)定义的数据结构称之为数据的逻辑结构。研究数 据结构的目的就是为了利用计算机对数据进行更为高效的处理，所以必须研究在计算机中如 何表示它，数据结构在计算机中的表示称为数据的物理结构。 1.2.4数据的物理结构 如果在机器语言的层面上讨论，什麼都是用"O"1"来表示。本课程在高级语言JAVA语 言层面上讨论，研究的是数据元素以及它们之间的关系在JAVA虚拟处理器中的表示。 1、数据元素的表示 单个数据项组成的数据元素利用JAVA语言固有的基本数据类型来表示。JAVA语言固有 的基本数据类型：整型、字符型、字符串型、双精度型等等。 例如：复数数据结构中的数据元素可用JAVA语言固有的双精度型型表示。由多个数据 项组成的数据元素利用JVA语言中的自己定义的类或结构来表示。 2、数据元素之间关系的表示 顺序存储：把数据元素按一定的规则放在一组地址连续的存储单元中，通过元素的存储 位置来体现数据元素之间的逻辑关系。逻辑上相邻的数据元素存储位置上也相邻。 以线性数据结构abcd为例： 线性数据结构abcd的顺序存储，把数据元素abcd放在一组地址连续的存储单元中，通 过元素的存储地址是否相邻来表示数据元素在逻辑上是否相邻：如图16所示： 存储地址 内存单元 图1一6顺序存储 链式存储：把数据元素结点中加一个引用域，通过指示元素存储地址的引用（©语言称 为指针)来体现数据元素的逻辑关系。逻辑上相邻的数据元素物理位置上不一定相邻。 线性数据结构abcd的顺序存储，把数据元素结点中加一个引用域，通过指示元素存储地 址的引用（©语言称为指针）来体现数据元素的逻辑关系。逻辑上相邻的数据元素物理位置

4 述的是数据元素之间的逻辑关系（{〈C1，C2〉}，是一种有序关系，C1 和 C2 不能互换）； 并不涉及在计算机中如何表示它，把(D，S)定义的数据结构称之为数据的逻辑结构。 研究数 据结构的目的就是为了利用计算机对数据进行更为高效的处理，所以必须研究在计算机中如 何表示它，数据结构在计算机中的表示称为数据的物理结构。 1.2.4 数据的物理结构 如果在机器语言的层面上讨论，什麽都是用"0""1" 来表示。本课程在高级语言-JAVA 语 言层面上讨论，研究的是数据元素以及它们之间的关系在 JAVA 虚拟处理器中的表示。 1、数据元素的表示 单个数据项组成的数据元素利用 JAVA 语言固有的基本数据类型来表示。JAVA 语言固有 的基本数据类型：整型、字符型、字符串型、双精度型等等。 例如：复数数据结构中的数据元素可用 JAVA 语言固有的双精度型型表示。由多个数据 项组成的数据元素利用 JAVA 语言中的自己定义的类或结构来表示。 2、数据元素之间关系的表示 顺序存储：把数据元素按一定的规则放在一组地址连续的存储单元中，通过元素的存储 位置来体现数据元素之间的逻辑关系。逻辑上相邻的数据元素存储位置上也相邻。 以线性数据结构 abcd 为例： a b c d 线性数据结构 abcd 的顺序存储，把数据元素 abcd 放在一组地址连续的存储单元中，通 过元素的存储地址是否相邻来表示数据元素在逻辑上是否相邻；如图 1-6 所示： 图 1－6 顺序存储 链式存储：把数据元素结点中加一个引用域，通过指示元素存储地址的引用（c 语言称 为指针）来体现数据元素的逻辑关系。逻辑上相邻的数据元素物理位置上不一定相邻。 线性数据结构 abcd 的顺序存储，把数据元素结点中加一个引用域，通过指示元素存储地 址的引用（c 语言称为指针）来体现数据元素的逻辑关系。逻辑上相邻的数据元素物理位置

上不一定相邻。如图1-7所示： head a→b□c□→d 存储地址 内容 直接后继存储地 100 b 120 120 160 首元泰位置， 144 100 160 NULL 图1一7链式存储 1.2.5抽象数据类型ADT 抽象数据类型就是在数据的逻辑结构基础上加上一组操作。为什麽还要研究操作呢？因 为针对不同的数据类型，定义于其上的操作也不一样。以JAVA语言中的int,string,Boolean 数据结构为例：lnt:有加、减、乘、除等操作.String:有取子串等操作Boolean有与、或、 非操作 在后面的章节中，研究每一种数据结构，都是从抽象数据类型开始。 和数据结构的形式定义相对应，抽象数据类型可用以下三元组表示ADT=D,S,P; 其中D是数据对象，S是D上的关系集，P是对D的基本操作集。本书采用以下格 式定义抽象数据类型： ADT抽象数据类型{ 数据对象： 基本操作： }ADT抽象数据类型名 其中基本操作的定义： 基本操作名（参数表） 初始条件： "初始条件“描述了操作执行之前数据结构和参数应满足的条件，若不满足，则操作失败， 并返回相应出错信息。"操作结果“说明了操作正常完成之后，数据结构的变化状况和英返回 的结果。若初始条件为空，则省略之。 5

5 上不一定相邻。如图 1-7 所示： head a b c d 图 1－7 链式存储 1.2.5 抽象数据类型 ADT 抽象数据类型就是在数据的逻辑结构基础上加上一组操作。为什麽还要研究操作呢？因 为针对不同的数据类型，定义于其上的操作也不一样。以 JAVA 语言中的 int，string，Boolean 数据结构为例：Int：有加、减、乘、除等操作.String：有取子串等操作.Boolean 有与、或、 非操作. 在后面的章节中，研究每一种数据结构，都是从抽象数据类型开始。 和数据结构的形式定义相对应，抽象数据类型可用以下三元组表示 ADT={D, S, P} 其中 D 是数据对象，S 是 D 上的关系集， P 是对 D 的基本操作集。本书采用以下格 式定义抽象数据类型： ADT 抽象数据类型{ 数据对象： 数据关系： 基本操作： }ADT 抽象数据类型名 其中基本操作的定义： 基本操作名（参数表） 初始条件： 操作结果： "初始条件"描述了操作执行之前数据结构和参数应满足的条件，若不满足，则操作失败， 并返回相应出错信息。"操作结果"说明了操作正常完成之后，数据结构的变化状况和英返回 的结果。若初始条件为空，则省略之