中国科学院数学与系统科学研究院：《高级计量经济学》课程教学资源（课件讲稿）第三章 Classical Linear Regression Model

中国科学院数学与系统科学研究院 Academy of Mathematics and Systems Science Chinese Academy of Sciences Classical Linear Regression Model Professor Yongmiao Hong March 24.2021

Classical Linear Regression Model Professor Yongmiao Hong March 24, 2021

CONTENTS 3.1 Framework and Assumptions 3.2 Ordinary Least Squares (OLS)Estimation 3.3 Goodness of Fit and Model Selection Criteria 3.4 Consistency and Efficiency of OLS 3.5 Sampling Distribution of OLS 3.6 Variance Estimation for OLS 3.7 Hypothesis Testing ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 2

ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 2 3.1 Framework and Assumptions 3.2 Ordinary Least Squares (OLS) Estimation 3.3 Goodness of Fit and Model Selection Criteria 3.4 Consistency and Efficiency of OLS 3.5 Sampling Distribution of OLS 3.6 Variance Estimation for OLS 3.7 Hypothesis Testing CONTENTS

CONTENTS 3.8 Applications 3.9 Generalized Least Squares (GLS) Estimation 3.10 Conclusion ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 3

ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 3 3.8 Applications 3.9 Generalized Least Squares (GLS) Estimation 3.10 Conclusion CONTENTS

Framework and Assumptions Suppose we have an observed random sample {Z1 of size n,where Zt =(Yt;X)',Yt is a scalar,Xt =(1,Xit;X2t,..Xit)'is a (k+1)x 1 vector,t is an index(either cross-sectional unit or time period)for observa- tions,and n is the sample size.We are interested in the conditional mean E(YiXt)using an observed realization (i.e.,a data set)of the random sample (rt,xi',t =1,....n. Throughout,we set K=k+1,the number of regressors which contains k economic variables and an intercept. Assumptions of the classical linear regression theory. Assumption 3.1 [Linearity]: Z=(Yi,X)')1 is an observable random sample of size n,with Y=XtB°+et, t=1,,n, where Bo is a k x 1 unknown parameter vector,and et is an unobservable disturbance. ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 4

ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 4 Framework and Assumptions Assumption 3.1

Framework and Assumptions Questions: Does Assumption 3.1 imply a causal relationship from Xt to Yi? Not necessarily.As Kendall and Stuart (1961,Vol.2,Ch.26,p.279)point out,"a statistical relationship,however strong and however suggestive, can never establish causal connection.Our ideas of causation must come from outside statistics ultimately,from some theory or other." Denote Y= (Yi,,Yn)', n×1, E= (e1,,en)/, n×1, X=(X1,,Xm), n×K. where the t-th row of X isX=(1,Xit,...,Xit). With these matrix notations,we have a compact expression for Assumption 3.1: Y= XB°+e, n×1=(n×K)(K×1)+n×1. ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 5

ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 5 Framework and Assumptions  Questions:

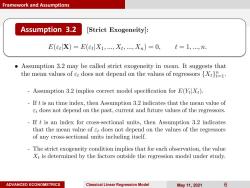
Framework and Assumptions Assumption 3.2 [Strict Exogeneity]: E(et X)=E(et X1;...Xi;...,Xn)=0, t=1,,n. Assumption 3.2 may be called strict exogeneity in mean.It suggests that the mean values of et does not depend on the values of regressors {X1. Assumption 3.2 implies correct model specification for E(YXt). If t is an time index,then Assumption 3.2 indicates that the mean value of et does not depend on the past,current and future values of the regressors. If t is an index for cross-sectional units,then Assumption 3.2 indicates that the mean value of et does not depend on the values of the regressors of any cross-sectional units including itself. The strict exogeneity condition implies that for each observation,the value Xt is determined by the factors outside the regression model under study. ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 6

ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 6 Framework and Assumptions Assumption 3.2

Framework and Assumptions Assumption 3.2 [Strict Exogeneity]: E(et X)=E(et X1,...,Xt;..,Xn)=0,t=1,...,n. - Under Assumption 3.2,we have E(Xset)=0 for any (t,s),where t,s E 1,...,n.This follows because E(XsEt) =EE(Xset X)] EXgE(et X E(Xs·0) 三 0. Given E(et)=0,E(Xset)=0 implies cov(Xs,Et)=0 for all t,s E {1,,n Because X contains regressors {Xs}for both s t,Assumption 3.2 essentially requires that the error et do not depend on both the past and future values of regressors if t is a time index.This rules out dynamic time series models for which et may be correlated with the future values of regressors. ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 7

ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 7 Framework and Assumptions Assumption 3.2

Framework and Assumptions Example 1 [Autoregressive (AR)Model]: .Consider an AutoRegressive AR(1)model Yi Bo+B1Yi-1+6t, t=1,,n, XB+Et, {et}~IID(0,o2), where Xt=(1,Yi-1)'. This is a dynamic regression model because the term BiY-1 represents the “memory”or“feedback'”of the past into the present value of the process, which induces a correlation between Yt and the past. The disturbance et can be viewed as representing the effect of "new infor- mation"that is revealed at time t.Any information that is truly new can- not be anticipated so that the effects of today's new information should be unrelated to the effects of yesterday's news in the sense that E(tXt)=0. ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 8

ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 8 Framework and Assumptions Example 1

Framework and Assumptions Example 1 [Autoregressive (AR)Model]: .Consider an AutoRegressive AR(1)model Yt Bo+B1Yi-1+Et, t=1,,n, XB+Et, {et}~IID(0,o2), where Xt =(1,Yi-1). Obviously,E(Xiet)=E(X:)E(et)=0 but E(Xt+1et)0.Thus,we have E(etX)0,and so Assumption 3.2 does not hold.Here,the lagged de- pendent variable Yi-1 in the regressor vector X:is called a predetermined variable,since it is orthogonal to st but depends on the past history of {et}. ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 9

ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 9 Framework and Assumptions Example 1

Framework and Assumptions Example 1 [Autoregressive (AR)Model]: In econometrics,there are various alternative definitions of exogeneity. For example,one definition assumes that st and X are independent. One example is that X is nonstochastic.This rules out conditional het- eroskedasticity (i.e.,var(et X)depends on X). The case that s and X are independent or X is nonstochastic is called strong exogeneity. ADVANCED ECONOMETRICS Classical Linear Regression Model May11,2021 10

ADVANCED ECONOMETRICS Classical Linear Regression Model May 11, 2021 10 Framework and Assumptions Example 1