福建农林大学：《试验设计与统计分析》课程教学课件（PPT讲稿）第3章 概率与抽样分布 Probability and Sampling Distributions

第3章概率与抽样分布 Probability and Sampling Distributions

第3章 概率与抽样分布 Probability and Sampling Distributions

Section 3.1 Random Variables 随机变量

Section 3.1 Random Variables 随机变量

一、频率与概率frequency and probability 事件的实际发生率称为频率。设在相同 条件下，独立重复进行n次试验，事件A出现 f次，则事件A出现的频率为f升n。 概率：随机事件发生的可能性大小，用 大写的P表示；取值[0,1]

事件的实际发生率称为频率。设在相同 条件下，独立重复进行n次试验，事件A出现 f 次，则事件A出现的频率为f/n。 概率：随机事件发生的可能性大小，用 大写的P 表示；取值[0，1]。 一、频率与概率frequency and probability

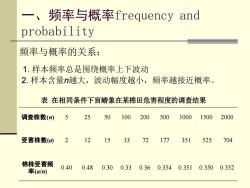
一、频率与概率frequency and probability 频率与概率的关系： 1.样本频率总是围绕概率上下波动 2.样本含量n越大，波动幅度越小，频率越接近概率。 表在相同条件下盲蝽象在某棉田危害程度的调查结果 调查株数(n) 5 25 50100 200 500 1000 1500 2000 受害株数(@ 2 12 153372177 351 525 704 棉株受害频 率(alnm) 0.400.480.300.330.360.3540.3510.3500.352

1. 样本频率总是围绕概率上下波动 2. 样本含量n越大，波动幅度越小，频率越接近概率。 频率与概率的关系： 调查株数(n) 5 25 50 100 200 500 1000 1500 2000 受害株数(a) 2 12 15 33 72 177 351 525 704 棉株受害频 率(a/n) 0.40 0.48 0.30 0.33 0.36 0.354 0.351 0.350 0.352 表 在相同条件下盲蝽象在某棉田危害程度的调查结果 一、频率与概率frequency and probability

一、 频率与概率frequency and probability 小概率原理 若事件A发生的概率较小，如小于0.05或0.01，则认为 事件A在一次试验中不太可能发生，这称为小概率事件实际 不可能性原理，简称小概率原理。这里的0.05或0.01称为小 概率标准，农业试验研究中通常使用这两个小概率标准

一、频率与概率frequency and probability 小概率原理 若事件A发生的概率较小，如小于0.05或0.01，则认为 事件A在一次试验中不太可能发生，这称为小概率事件实际 不可能性原理，简称小概率原理。这里的0.05或0.01称为小 概率标准，农业试验研究中通常使用这两个小概率标准

二、随机变量 >用以记录随机试验结果(outcome))的变量，称 为随机变量(random variable),用大写英文 字母X,Y等代表。 >随机变量X的概率分布，表达X的可能取值 和取这些值的概率规则

二、随机变量 ➢ 用以记录随机试验结果(outcome)的变量，称 为随机变量(random variable)，用大写英文 字母X, Y 等代表。 ➢ 随机变量X的概率分布，表达 X 的可能取值 和取这些值的概率规则

二、随机变量 离散型和连续型随机变量 >随机变量的可能取值是离散的数字，如计数型或分类 型等，称为离散型随机变量(discrete random variable)。 ■{0,1，9}。 ·20次实验中成功的次数，二项式分布。 >随机变量的可能取值是某一实数的区间，如“大于0” 或“-22之间”等，称为连续型随机变量 (continuous random variable). ■正态随机变量

离散型和连续型随机变量 ➢ 随机变量的可能取值是离散的数字，如计数型或分类 型等，称为离散型随机变量(discrete random variable)。 ▪ {0, 1,., 9} 。 ▪ 20次实验中成功的次数， 二项式分布。 ➢ 随机变量的可能取值是某一实数的区间，如“大于0” 或“-2~2之间”等，称为连续型随机变量 (continuous random variable)。 ▪ 正态随机变量 二、随机变量

三、离散型随机变量的概率分布 >列出离散型随机变量X的所有可能取值 >列出随机变量取这些值的概率 >通常用下面的表格来表示 X=xi X12.n P(X=x)-Pi P1yP2y.yPn >P(仪=x;)=p:称为离散型随机变量的概率函数 p,≥O

三、离散型随机变量的概率分布 X = xi x1 ，x2，. ，xn P(X =xi )=pi p1 ，p2，. ，pn 1 0 1 i n i i p p =   = ➢ 列出离散型随机变量X的所有可能取值 ➢ 列出随机变量取这些值的概率 ➢ 通常用下面的表格来表示 ➢ P(X =xi)=pi称为离散型随机变量的概率函数

四、连续型随机变量的概率密度 >若观察资料数量够大，则直方图（组数适当增 加)的整体形态可用一近似的平滑曲线显示。 >直方图中纵轴改为次数比例，则该平滑曲线 称为密度曲线(density curve)

四、连续型随机变量的概率密度 ➢ 若观察资料数量够大，则直方图(组数适当增 加)的整体形态可用一近似的平滑曲线显示。 ➢ 直方图中纵轴改为次数比例，则该平滑曲线 称为密度曲线(density curve)

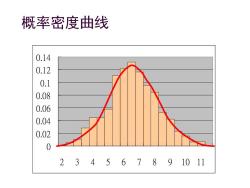
概率密度曲线 0.14 0.12 0.1 0.08 0.06 0.04 0.02 0 234567891011

概率密度曲线 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 2 3 4 5 6 7 8 9 10 11