《数据结构》课程教学资源（PPT课件）第七章 图（7.1 概述 7.2 图的存储结构）

图第七章概述7.1·7.2图的存储结构邻接矩阵图类7.37.4图的遍历

第七章 图 • 7.1 概述 • 7.2 图的存储结构 • 7.3 邻接矩阵图类 • 7.4 图的遍历

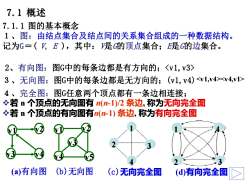
7.1 概述7.1.1图的基本概念1、图：由结点集合及结点间的关系集合组成的一种数据结构。记为G=（V，E），其中：V是G的顶点集合；G的边集合。2、有向图：图G中的每条边都是有方向的；3、无向图：图G中的每条边都是无方向的；（vl,v4)4、完全图：图G任意两个顶点都有一条边相连接：*若n个顶点的无向图有n(n-1)/2条边，称为无向完全图若n个顶点的有向图有n(n-1）条边，称为有向完全图Iv5V(a)有向图(b)无向图（c）无向完全图(d）有向完全图

7.1 概述 7.1.1 图的基本概念 １、图：由结点集合及结点间的关系集合组成的一种数据结构。 记为G＝( V, E )，其中：V是G的顶点集合；E是G的边集合。 v1 v2 v3 v4 2、有向图：图G中的每条边都是有方向的； ３、无向图：图G中的每条边都是无方向的；(v1,v4) ４、完全图：图G任意两个顶点都有一条边相连接； ❖若 n 个顶点的无向图有 n(n-1)/2 条边, 称为无向完全图 ❖若 n 个顶点的有向图有n(n-1) 条边, 称为有向完全图 1 2 3 1 4 2 3 4 (a)有向图 (b)无向图 (c)无向完全图 (d)有向完全图 v1 v2 v3 v4 v5

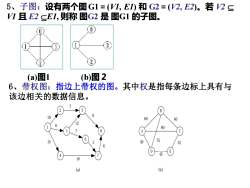
5、子图：设有两个图G1=(V1,EI)和G2=(V2,E2)。若V2 CV1且E2CE1,则称图G2是图G1的子图。(a)图1(b)图26、带权图：指边上带权的图。其中权是指每条边标上具有与该边相关的数据信息。10604080753015354516(a)(b)

5、子图：设有两个图G1＝(V1, E1) 和 G2＝(V2, E2)。若 V2  V1 且 E2 E1, 则称 图G2 是 图G1 的子图。 (a)图1 (b)图２ 6、带权图：指边上带权的图。其中权是指每条边标上具有与 该边相关的数据信息。 2 1 3 5 4 6 7 8 7 9 6 10 6 12 7 15 16 3 B A C D E 60 30 45 75 80 40 35 (a) (b)

7、路径：在图G（V、E)中，若从顶点V；出发，沿一些边经过顶点Vpl,Vp2,.Vpm，到达顶点vjo则称顶点序列（vi,Vpl,Vp2,…Vpm，y）_为从顶点vi到顶点v,的路径。路径长度：非带权图的路径长度是指此路径上边的条数；带权图的路径长度是指路径上各边的权之和。1060408075153035H4516(a)(b)8、简单路径：路径上各顶点V1,V2.Vm均不互相重复。9、回路：若路径上第一个顶点V1与最后一个顶点Vm重合，则称这样的路径为回路或环

７、路径：在图G＝(V, E)中,若从顶点 vi 出发,沿一些边经过 顶点vp1,vp2,.,vpm，到达顶点vj。则称顶点序列(vi,vp1,vp2,., vpm ,vj ) 为从顶点vi 到顶点 vj 的路径。 路径长度：非带权图的路径长度是指此路径上边的条数； 带权图的路径长度是指路径上各边的权之和。 ８、简单路径：路径上各顶点 v1 ,v2 ,.,vm 均不互相重复。 ９、回路：若路径上第一个顶点 v1 与最后一个顶点vm 重合，则 称这样的路径为回路或环。 2 1 3 5 4 6 7 8 7 9 6 10 6 12 7 15 16 3 B A C D E 60 30 45 75 80 40 35 (a) (b)

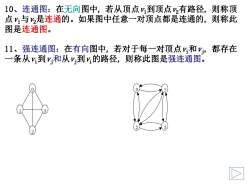
则称顶10、连通图：在无向图中，若从顶点v到顶点v有路径，点,与v,是连通的。如果图中任意一对顶点都是连通的，则称此图是连通图。都存在11、强连通图：在有向图中，若对于每一对顶点v;和vi,一条从V到v:和从v到v;的路径，则称此图是强连通图

10、连通图：在无向图中, 若从顶点v1到顶点v2有路径, 则称顶 点v1与v2是连通的。如果图中任意一对顶点都是连通的, 则称此 图是连通图。 11、强连通图：在有向图中, 若对于每一对顶点vi和vj, 都存在 一条从vi到vj和从vj到vi的路径, 则称此图是强连通图。 0 1 3 2 0 1 2 3

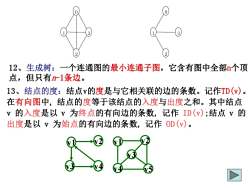
12、生成树：一个连通图的最小连通子图，它含有图中全部n个顶点，但只有n-1条边。13、结点的度：结点v的度是与它相关联的边的条数。记作TD(v）在有向图中，结点的度等于该结点的入度与出度之和。其中结点v 的入度是以 v为终点的有向边的条数，记作 ID(v);结点 的出度是以 V为始点的有向边的条数，记作OD（v）

12、生成树：一个连通图的最小连通子图，它含有图中全部n个顶 点，但只有n-1条边。 13、结点的度：结点v的度是与它相关联的边的条数。记作TD(v)。 在有向图中, 结点的度等于该结点的入度与出度之和。其中结点 v 的入度是以 v 为终点的有向边的条数, 记作 ID(v);结点 v 的 出度是以 v 为始点的有向边的条数, 记作 OD(v)。 0 1 3 2 0 1 3 2 v1 v2 v3 v4 v1 v2 v3 v4 v5

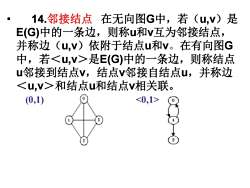
14.邻接结点在无向图G中，若（u,v）是E(G)中的一条边，则称u和v互为邻接结点，并称边（u,v）依附于结点u和v。在有向图G中，若是E(G)中的一条边，则称结点u邻接到结点V，结点v邻接自结点u，并称边和结点u和结点v相关联(0,1)2

• 14.邻接结点 在无向图G中，若（u,v）是 E(G)中的一条边，则称u和v互为邻接结点， 并称边（u,v）依附于结点u和v。在有向图G 中，若＜u,v＞是E(G)中的一条边，则称结点 u邻接到结点v，结点v邻接自结点u，并称边 ＜u,v＞和结点u和结点v相关联。 (0,1)

·7.1.2图的抽象数据类型数据集合：由一组结点集合{v}和一组边[e}集合组成。当为带权图时每条边上权w,还构成权集合{w}。操作集合：（1）初始化initiate(n)：（2）插入结点insertVertex(vertex)：(3）插入边insertEdge(v1,v2,weight)：(4）删除边deleteEdge(v1,v2)：（5）删除结点deleteVertex(vertex)：（6）第一个邻接结点getFirstVex(v)：（7）下一个邻接结点getNextVex(v1，v2)（8）遍历depthFirstSearch(vs)：

• 7.1.2 图的抽象数据类型 • 数据集合：由一组结点集合{vi }和一组边{ej }集合组成。 当为带权图时每条边上权wj还构成权集合{wj }。 • 操作集合： • （1）初始化initiate(n)： • （2）插入结点 insertVertex(vertex)： • （3）插入边insertEdge(v1, v2, weight)： • （4）删除边deleteEdge(v1, v2)： • （5）删除结点deleteVertex(vertex)： • （6）第一个邻接结点getFirstVex(v)： • （7）下一个邻接结点getNextVex(v1, v2)： • （8）遍历depthFirstSearch(vs)：

7. 2图的存储结构图的存储结构主要有邻接矩阵和邻接表两种。7.2.1图的邻接矩阵存储结构假设图G=(V,E)有n个结点，即V={v0,vl,.,vn-1}，E可用如下形式的矩阵A描述，对于A中的每一个元素aii，满足：若(y,V,)E或EE0否则由于矩阵A中的元素aii表示了结点vi和结点vi之间边的关系，或者说，A中的元素aii表示了结点vi和结点vi的邻接关系，所以矩阵A称作邻接矩阵

7.2 图的存储结构 图的存储结构主要有邻接矩阵和邻接表两种。 7.2.1 图的邻接矩阵存储结构       = 否则 若 或 0 1 (v ,v ) E v ,v E a i j i j i j 假设图G=(V,E)有n个结点，即V={v0,v1,.,vn-1}，E可 用如下形式的矩阵A描述，对于A中的每一个元素aij，满足： 由于矩阵A中的元素aij表示了结点vi和结点vj之间边的关 系，或者说，A中的元素aij表示了结点vi和结点vj的邻接关 系，所以矩阵A称作邻接矩阵

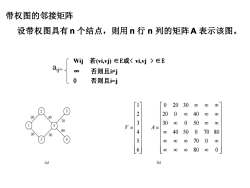
带权图的邻接矩阵设带权图具有n个结点，则用n行n列的矩阵A表示该图。若(vi,vi) EE或EEWij8否则且诗j0否则且i-j020300000804020208000807033080050808408050070480657008000808680088080(a)(b)

2 1 4 3 5 6                                       = 80 0 70 0 40 50 0 70 80 30 0 50 20 0 40 0 20 30 A                     = 6 5 4 3 2 1 V (a) (b) 20 40 30 50 70 80 带权图的邻接矩阵 设带权图具有 n 个结点，则用 n 行 n 列的矩阵A 表示该图。 aij= Wij 若(vi,vj) ∈E或 ∈E ∞ 否则且i=j 0 否则且i=j