《数据结构》课程授课教案（讲稿）第六章 树和二叉树 第一节 树 第二节 二叉树

课程名称：数据结构第10周，第10讲次摘要第六章树和二叉树授课题目（章、节）第一节树第二节二叉树【目的要求】通过本讲课程的学习，理解树和二叉树及其相关概念、树和二叉树的存储结构，理解树和二叉树是两种不同的树型结构，熟练掌握二叉树的五个性质。【重点】理解二叉树的相关概念，熟练掌握二叉树的五个性质【难点】二叉树性质的理解和熟练运用。内容【本讲课程的引入】从这一讲课起我们开始学习一种非线性结构一一树型结构，我们在第一讲课中提到过树型结构的特点是一对多的，也就是一个结点（除了根结点外）有一个直接前驱，有零个或多个直接后继，本讲我们主要学习关于树和二叉树的一些基本知识。【本讲课程的内容】第 6 章 树和二叉树6.1树6.1.1树的定义树是由n(n≥0)个结点组成的有限集合T。n=0的树称为空树；对n>0的树，有：(1)仅有一个特殊的结点称为根结点，根结点没有前驱结点：（2）当n>1时，除根结点外其余的结点分为m(m>0)个互不相交的有限集合T1,T2，，Tm，其中每个集合Ti本身又是一棵结构和树类似的子树。注意：树的定义具有递归性，即“树中还有树”。树的示例：(a)(b)只有根结点的树一般的树根一即根结点（没有前驱）叶子结点一即终端结点（没有后继）森林一指m棵不相交的树的集合（例如删除A后的子树个数）有序树一结点各子树从左至右有序，不能互换（左为第一）无序树结点各子树可互换位置。双亲结点即上层的那个结点（直接前驱）孩子结点即下层结点的子树的根（直接后继）兄弟结点同一双亲下的同层结点（孩子之间互称兄弟）祖先结点一即从根到该结点所经分支的所有结点

课程名称：数据结构 第 10 周，第 10 讲次 摘 要 授课题目（章、节） 第六章 树和二叉树 第一节 树 第二节 二叉树 【目的要求】通过本讲课程的学习，理解树和二叉树及其相关概念、树和二叉树的存储结构，理解树和二叉 树是两种不同的树型结构，熟练掌握二叉树的五个性质。 【重 点】理解二叉树的相关概念，熟练掌握二叉树的五个性质。 【难 点】二叉树性质的理解和熟练运用。 内 容 【本讲课程的引入】从这一讲课起我们开始学习一种非线性结构——树型结构，我们在第一讲 课中提到过树型结构的特点是一对多的，也就是一个结点（除了根结点外）有一个直接前驱， 有零个或多个直接后继，本讲我们主要学习关于树和二叉树的一些基本知识。 【本讲课程的内容】 第 6 章 树和二叉树 6.1 树 6.1.1 树的定义 树是由 n(n≥0)个结点组成的有限集合 T。n=0 的树称为空树；对 n>0 的树，有:(1)仅有一 个特殊的结点称为根结点，根结点没有前驱结点；(2)当 n>1 时，除根结点外其余的结点分为 m(m>0)个互不相交的有限集合 T1,T2，.，Tm，其中每个集合 Ti 本身又是一棵结构和树类似的 子树。 注意：树的定义具有递归性，即“树中还有树”。 树的示例： 根 ——即根结点(没有前驱) 叶子结点 ——即终端结点(没有后继) 森林 ——指 m 棵不相交的树的集合(例如删除 A 后的子树个数) 有序树 ——结点各子树从左至右有序，不能互换（左为第一） 无序树 ——结点各子树可互换位置。 双亲结点 ——即上层的那个结点(直接前驱) 孩子结点 ——即下层结点的子树的根(直接后继) 兄弟结点 ——同一双亲下的同层结点（孩子之间互称兄弟） 祖先结点 ——即从根到该结点所经分支的所有结点 A B C D E F G H I J K L A (a) (b) 只有根结点的树 一般的树

子孙结点一即以该结点为根的子树中的所有结点结点一即树的数据元素结点的度一结点挂接的子树数（有几个直接后继就是几度，亦称“次数”）结点的层次一一从根到该结点的层数（根结点算第0层）-终端结点即度为0的结点，即叶子分支结点一即度不为0的结点（也称为内部结点）树的度所有结点度中的最大值（Max（各结点的度)）树的深度指所有结点中最大的层数（Max（各结点的层次））6.1.2树的抽象数据类型数据集合：树的结点集合，每个结点由数据元素和构造数据元素之间关系的指针组成。操作集合：（1）双亲结点parent（）：把当前结点的双亲结点置为当前结点。（2）左孩子结点1eftChild（)：把当前结点的左孩子结点置为当前结点。（3）右兄弟结点rightSiblingO：把当前结点的右兄弟结点置为当前结点。（4）遍历树traverse（vs）：按某种遍历方法访问树的每个结点，且每个结点只访问一次。6.1.3树的存储结构1双亲表示法双亲表示法就是用指针表示出每个结点的双亲结点。对于使用仿真指针的双亲表示法来说，每个结点应有两个域，一个是数据元素域，另一个是指示其双亲结点在数组中下标序号的仿真指针域。树及其使用仿真指针的双亲表示法dataparentA0-10B1c0C2R3D1FE14F51G62(a)H74184(b)2孩子表示法

子孙结点 ——即以该结点为根的子树中的所有结点 结点 ——即树的数据元素 结点的度 ——结点挂接的子树数（有几个直接后继就是几度，亦称“次数”） 结点的层次——从根到该结点的层数（根结点算第 0 层） 终端结点 ——即度为 0 的结点，即叶子 分支结点 ——即度不为 0 的结点（也称为内部结点） 树的度 ——所有结点度中的最大值（Max{各结点的度}） 树的深度 ——指所有结点中最大的层数（Max{各结点的层次}） 6.1.2 树的抽象数据类型 数据集合 ：树的结点集合，每个结点由数据元素和构造数据元素之间关系的指针组成。 操作集合 ：（1）双亲结点 parent() ：把当前结点的双亲结点置为当前结点。 （2）左孩子结点 leftChild()：把当前结点的左孩子结点置为当前结点。 （3）右兄弟结点 rightSibling() ：把当前结点的右兄弟结点置为当前结点。 （4）遍历树 traverse(vs) ：按某种遍历方法访问树的每个结点，且每个结点只访问一次。 6.1.3 树的存储结构 1 双亲表示法 双亲表示法就是用指针表示出每个结点的双亲结点。 对于使用仿真指针的双亲表示法来说，每个结点应有两个域，一个是数据元素域，另一个 是指示其双亲结点在数组中下标序号的仿真指针域。 树及其使用仿真指针的双亲表示法 2 孩子表示法 A D E F G C H I B (a) 0 1 2 3 4 5 6 7 8 A B C D E F G H I data parent -1 0 0 1 1 1 2 4 4 (b)

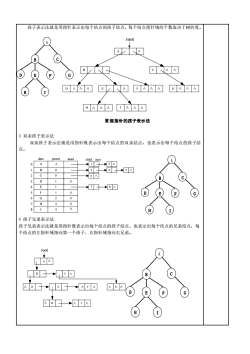
孩子表示法就是用指针表示出每。每个结点指针域的个数取决于树的度。4rootACAEAGAHAAAIIAA常规指针的孩子表示法3双亲孩子表示法双亲孩子表示法就是用指针既表示出每个结点的双亲结点，也表示出每个结点的孩子结点。dataparentheadchildnext-1-A03B0cc3DA-78AE5ΛF7026H4Λ7Λ4814孩子兄弟表示法孩子兄弟表示法就是用指针既表示出每个结点的孩子结点，也表示出每个结点的兄弟结点，每个结点的左指针域指向第一个孩子，右指针域指向右兄弟。root+IAAADEAAAG

孩子表示法就是用指针表示出每个结点的孩子结点。每个结点指针域的个数取决于树的度。 3 双亲孩子表示法 双亲孩子表示法就是用指针既表示出每个结点的双亲结点，也表示出每个结点的孩子结 点。 4 孩子兄弟表示法 孩子兄弟表示法就是用指针既表示出每个结点的孩子结点，也表示出每个结点的兄弟结点，每 个结点的左指针域指向第一个孩子，右指针域指向右兄弟。 A D E F G C H I B A B C D E F G H I ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ root ∧ 常规指针的孩子表示法 0 1 2 3 4 5 6 7 8 A B C D E F G H I 1 -1 2 4 4 data parent 0 ∧ ∧ ∧ ∧ ∧ 1 3 2 4 5 6 7 8 ∧ ∧ ∧ ∧ head child next 0 1 1 A D E F G C H I B A B C D E F G H I ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ root ∧ A D E F G C H I B

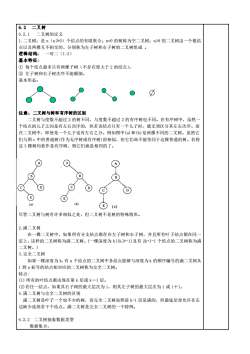
6.2二叉树6.2.1二叉树的定义1.二叉树：是n（n≥0）个结点的有限集合。n=0的树称为空二叉树：n>0的二叉树由一个根结点以及两棵互不相交的、分别称为左子树和右子树的二叉树组成。逻辑结构：一对二（1:2）基本特征：①每个结点最多只有两棵子树（不存在度大于2的结点）：②左子树和右子树次序不能颠倒。基本形态：C注意：二叉树与树和有序树的区别二叉树与度数不超过2的树不同，与度数不超过2的有序树也不同。在有序树中，虽然一个结点的儿子之间是有左右次序的，但若该结点只有一个儿子时，就无须区分其左右次序。而在二叉树中，即使是一个儿子也有左右之分。例如图中（a）和（b）是两棵不同的二叉树。虽然它们与图c中的普通树（作为无序树或有序树）很相似，但它们却不能等同于这棵普通的树。若将这3棵树均看作是有序树，则它们就是相同的了。B(b)(a)?(c)尽管二叉树与树有许多相似之处，但二叉树不是树的特殊情形。2.满二叉树在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子结点都在同一层上，这样的二叉树称为满二叉树。（一棵深度为k（(k≥-1)且有2k+1-1个结点的二叉树称为满二叉树。）3.完全二叉树如果一棵深度为k，有n个结点的二叉树中各结点能够与深度为k的顺序编号的满二叉树从1到n标号的结点相对应的二叉树称为完全二叉树。特点：(1)所有的叶结点都出现在第k层或k一1层。(2)若任一结点，如果其右子树的最大层次为i，则其左子树的最大层次为i或i十1。4.满二叉树与完全二叉树的区别满二叉树是叶子一个也不少的树，而完全二叉树虽然前k-1层是满的，但最底层却允许在右边缺少连续若于个结点。满二叉树是完全二叉树的一个特例。6.2.2二叉树抽象数据类型数据集合：

6.2 二叉树 6.2.1 二叉树的定义 1.二叉树：是 n（n≥0）个结点的有限集合。n=0 的树称为空二叉树；n>0 的二叉树由一个根结 点以及两棵互不相交的、分别称为左子树和右子树的二叉树组成 。 逻辑结构： 一对二（1:2） 基本特征: ① 每个结点最多只有两棵子树（不存在度大于 2 的结点）； ② 左子树和右子树次序不能颠倒。 基本形态： 注意：二叉树与树和有序树的区别 二叉树与度数不超过 2 的树不同，与度数不超过 2 的有序树也不同。在有序树中，虽然一 个结点的儿子之间是有左右次序的，但若该结点只有一个儿子时，就无须区分其左右次序。而 在二叉树中，即使是一个儿子也有左右之分。例如图中(a)和(b)是两棵不同的二叉树。虽然它 们与图 c 中的普通树(作为无序树或有序树)很相似，但它们却不能等同于这棵普通的树。若将 这 3 棵树均看作是有序树，则它们就是相同的了。 尽管二叉树与树有许多相似之处，但二叉树不是树的特殊情形。 2.满二叉树 在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子结点都在同一 层上，这样的二叉树称为满二叉树。(一棵深度为 k((k≥-1)且有 2k+1-1 个结点的二叉树称为满 二叉树。) 3.完全二叉树 如果一棵深度为 k，有 n 个结点的二叉树中各结点能够与深度为 k 的顺序编号的满二叉树从 1 到 n 标号的结点相对应的二叉树称为完全二叉树。 特点: (1) 所有的叶结点都出现在第 k 层或 k－1 层。 (2)若任一结点，如果其右子树的最大层次为 i，则其左子树的最大层次为 i 或 i＋1。 4.满二叉树与完全二叉树的区别 满二叉树是叶子一个也不少的树，而完全二叉树虽然前 k-1 层是满的，但最底层却允许在右 边缺少连续若干个结点。满二叉树是完全二叉树的一个特例。 6.2.2 二叉树抽象数据类型 数据集合： (c)

二叉树的结点集合，每个结点由数据元素和构造数据元素之间关系的指针组成，操作集合：（1）双亲结点parent（：（2）左孩子结点leftChild（）（3）右孩子结点rightChild）（4）左插入结点insertLeftNode（x）（5）右插入结点insertRightNode（x）：（6）左删除子树deleteLeftTree（（7）右删除子树deleteRightTree（）（8）遍历二叉树traverse（vs）6.2.3二叉树的性质性质1：在一棵非空二叉树的第i层上至多有2°个结点（i≥0）。性质2:深度为k的二叉树至多有2**-1个结点(k≥-1)。性质3：对于任何一棵非空的二叉树，若度为2的结点数有n2个，则叶子数（n0）必定为n2十1（即n0=n2+1)证明：：二叉树中全部结点数n=n0+nl+n2（叶子数+1度结点数+2度结点数）又：二叉树中全部结点数n=B+1（总分支数+根结点）（除根结点外，每个结点必有一个直接前趋，即一个分支）而总分支数B=n1+2n2（1度结点必有1个直接后继，2度结点必有2个）三式联立可得：n0+n1+n2=n1+2n2+1，即n0=n2+1对于两种特殊形式的二义树（满二义树和完全二义树），还特别具备以下2个性质：性质4：具有n个结点的完全二叉树的深度k必为「1og2(n+1)-1（假定k为0时表示此二叉树仅有根结点）证明：根据性质2，深度为k的二叉树最多只有2k+1-1个结点，且完全二叉树的定义是与同深度的满二叉树前面编号相同，即它的总结点数n位于k层和k-1层满二叉树容量之间，即2(k-1)+1-10，则其双亲是结点（i-1)/2（“/”表示整除）。(2)如果2i+1≥n，则结点i为叶子结点，无左孩子：否则，其左孩子是结点2i+1。（3）如果2i十2≥n，则结点i无右孩子；否则，其右孩子是结点2i+2。可根据归纳法证明。6.2.4二叉树的存储结构二义树的存储结构主要有三种：顺序存储结构、链式存储结构和仿真指针存储结构。1.二叉树的顺序存储结构完全二叉树的结点可按从上至下和从左至右的次序存储在一维数组中，其结点之间的关系可由公式计算得到，这就是二叉树的顺序存储结构。下图在数组中的存储结构为：

二叉树的结点集合，每个结点由数据元素和构造数据元素之间关系的指针组成。 操作集合： （1）双亲结点 parent()： （2）左孩子结点 leftChild() （3）右孩子结点 rightChild() （4）左插入结点 insertLeftNode(x) （5）右插入结点 insertRightNode(x)： （6）左删除子树 deleteLeftTree() （7）右删除子树 deleteRightTree() （8）遍历二叉树 traverse(vs) 6.2.3 二叉树的性质 性质 1:在一棵非空二叉树的第 i 层上至多有 2 i 个结点（i≥0）。 性质 2:深度为 k 的二叉树至多有 2 k+1 -1 个结点(k≥-1)。 性质 3: 对于任何一棵非空的二叉树，若度为 2 的结点数有 n2 个，则叶子数（n0）必定为 n2＋ 1 （即 n0=n2+1） 证明： ∵ 二叉树中全部结点数 n＝n0+n1+n2(叶子数＋1 度结点数＋2 度结点数) 又∵二叉树中全部结点数 n＝B+1 ( 总分支数＋根结点 ) （除根结点外，每个结点必有一个直接前趋，即一个分支） 而 总分支数 B= n1+2n2 (1 度结点必有 1 个直接后继，2 度结点必有 2 个) 三式联立可得： n0+n1+n2= n1+2n2 +1, 即 n0=n2+1 对于两种特殊形式的二叉树（满二叉树和完全二叉树），还特别具备以下 2 个性质： 性质 4: 具有 n 个结点的完全二叉树的深度 k 必为「log2(n+1)-1 (假定 k 为 0 时表示此二叉树仅有根结点) 证明：根据性质 2，深度为 k 的二叉树最多只有 2k+1-1 个结点，且完全二叉树的定义是与同深 度的满二叉树前面编号相同，即它的总结点数 n 位于 k 层和 k-1 层满二叉树容量之间， 即 2(k-1)+1-10，则其双亲是结点(i-1)/2(“/”表 示整除）。 (2)如果 2i+1≥n，则结点 i 为叶子结点，无左孩子；否则，其左孩子是结点 2i+1。 (3)如果 2i＋2≥n，则结点 i 无右孩子；否则，其右孩子是结点 2i＋2。 可根据归纳法证明。 6.2.4 二叉树的存储结构 二叉树的存储结构主要有三种：顺序存储结构、链式存储结构和仿真指针存储结构。 1. 二叉树的顺序存储结构 完全二叉树的结点可按从上至下和从左至右的次序存储在一维数组中，其结点之间的关系 可由公式计算得到，这就是二叉树的顺序存储结构。下图在数组中的存储结构为：

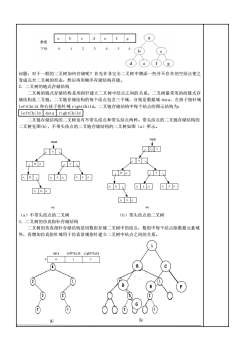
数组下标问题：对于一般的二叉树如何存储呢？首先在非完全二叉树中增添一些并不存在的空结点使之变成完全二叉树的形态，然后再用顺序存储结构存储。2.二叉树的链式存储结构二叉树的链式存储结构是用指针建立二叉树中结点之间的关系。二叉树最常用的的链式存储结构是二叉链。二叉链存储结构的每个结点包含三个域，分别是数据域data、左孩子指针域leftChild和右孩子指针域rightChild。二叉链存储结构中每个结点的图示结构为：leftChilddatarightChild二叉链存储结构的二叉树也有不带头结点和带头结点两种。带头结点的二叉链存储结构的二叉树见图（b），不带头结点的二叉链存储结构的二叉树如图（a）所示。rootroott+AAABKLCBAcAEAAFASADAAAGAAGA(a)(b)（a）不带头结点的二叉树（b）带头结点的二叉树3.二叉树的仿真指针存储结构二叉树的仿真指针存储结构是用数组存储二叉树中的结点，数组中每个结点除数据元素域外，再增加仿真指针域用于仿真常规指针建立二叉树中结点之间的关系。dataleftChildrightChild10(b)(a)

问题：对于一般的二叉树如何存储呢？首先在非完全二叉树中增添一些并不存在的空结点使之 变成完全二叉树的形态，然后再用顺序存储结构存储。 2. 二叉树的链式存储结构 二叉树的链式存储结构是用指针建立二叉树中结点之间的关系。二叉树最常用的的链式存 储结构是二叉链。二叉链存储结构的每个结点包含三个域，分别是数据域 data、左孩子指针域 leftChild 和右孩子指针域 rightChild。二叉链存储结构中每个结点的图示结构为： leftChild data rightChild 二叉链存储结构的二叉树也有不带头结点和带头结点两种。带头结点的二叉链存储结构的 二叉树见图(b)，不带头结点的二叉链存储结构的二叉树如图（a）所示。 （a）不带头结点的二叉树 （b）带头结点的二叉树 3. 二叉树的仿真指针存储结构 二叉树的仿真指针存储结构是用数组存储二叉树中的结点，数组中每个结点除数据元素域 外，再增加仿真指针域用于仿真常规指针建立二叉树中结点之间的关系。 A B C D E F G ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ (a) A B C D E F G ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ (b) root root ∧ A D G E C F B

【本讲课程的小结】这一次课内容比较多，基本都是一些基本的概念和性质，对于概念性的内容重在理解，不要求死记硬背，但是对于二叉树的性质要求熟练掌握。【本讲课程的作业】若一棵度为4的树中度为1、2、3、4的结点个数分别为4、3、2、2，则该树叶子结点的个数是多少？总结点个数是多少？

【本讲课程的小结】这一次课内容比较多，基本都是一些基本的概念和性质，对于概念性的内 容重在理解，不要求死记硬背，但是对于二叉树的性质要求熟练掌握。 【本讲课程的作业】 若一棵度为 4 的树中度为 1、2、3、4 的结点个数分别为 4、3、2、2，则该树叶子结点的个数是 多少？总结点个数是多少？