《数据结构》课程授课教案（讲稿）第二章 线性表 第一节 线性表 第二节 顺序表

课程名称：数据结构第2周，第2讲次摘要第二章线性表授课题目（章、节）第一节线性表第二节顺序表【目的要求】通过本讲课程的学习，了解线性表的定义和抽象数据类型，掌握顺序表存储结构的特点，顺序表类的设计方法，特别是要求掌握顺序表的插入和删除操作。【重点】掌握顺序表存储结构的特点，以及顺序表类的各种操作。【难点】顺序表的插入和删除操作，以及插入和删除操作的时间复杂度分析内容【本讲课程的引入】线性表是一种最简单的、最常用的线性结构。在这一章中我们将从线性表的逻辑结构，物理结构（存储结构），线性表的操作三个方面讨论线性表这种线性结构。这一次课我们主要学习的是线性表的逻辑结构定义，以及线性表的顺序存储一一顺序表的存储特点，顺序表操作的具体实现，特别是如何在顺序表中插入和删除数据元素。【本讲课程的内容】2.1线性表2.1.1线性表的定义1.首先回顾线性结构的定义如果一个数据元素序列满足（1）除第一个和最后一个数据元素外，每个数据元素只有一个前驱数据元素和一个后继数据元素；（2）第一个数据元素没有前驱数据元素：（3）最后一个数据元素没有后继数据元素。则称这样的数据结构为线性结构。2.线性表定义线性表是一种可以在任意位置进行插入和删除数据元素操作的、由n（n≥O）个相同类型数据元素ao，al，a2，..an-1组成的线性结构。一个有n个数据元素ao，al，a2，，an-1的线性表通常用符号（a0，al，a2，..,an-1）表示，其中符号ai（0≤i≤n-1）表示第i个抽象数据元素。空线性表用符号（）表示。2.1.2线性表抽象数据类型数据集合线性表的数据元素集合可以表示为序列ao，al，a2，..an-1，每个数据元素的数据类型可以是任意的类类型。操作集合（1）求当前数据元素个数size（)：求线性表的当前数据元素个数并由函数返回。（2）插入数据元素insert（i，obj)：注意i的合法取值（3）删除数据元素delete（i）：所删除的数据元素由函数返回。删除的合法位置（4）取数据元素getData(i）：取线性表的第i个数据元素，所取的数据元素由函数返回。（5）线性表是否空isEmpty（)：线性表中的当前数据元素个数size（）是否为0。如果size（）为0函数返回true，否则返回false

课程名称：数据结构 第 2 周，第 2 讲次 摘 要 授课题目（章、节） 第二章 线性表 第一节 线性表 第二节 顺序表 【目的要求】通过本讲课程的学习，了解线性表的定义和抽象数据类型，掌握顺序表存储结构的特点，顺序 表类的设计方法，特别是要求掌握顺序表的插入和删除操作。 【重 点】掌握顺序表存储结构的特点，以及顺序表类的各种操作。 【难 点】顺序表的插入和删除操作，以及插入和删除操作的时间复杂度分析。 内 容 【本讲课程的引入】线性表是一种最简单的、最常用的线性结构。在这一章中我们将从线 性表的逻辑结构，物理结构（存储结构），线性表的操作三个方面讨论线性表这种线性结构。 这一次课我们主要学习的是线性表的逻辑结构定义，以及线性表的顺序存储——顺序表的 存储特点，顺序表操作的具体实现，特别是如何在顺序表中插入和删除数据元素。 【本讲课程的内容】 2.1 线性表 2.1.1 线性表的定义 1.首先回顾线性结构的定义 如果一个数据元素序列满足： （1）除第一个和最后一个数据元素外，每个数据元素只有一个前驱数据元素和一个后 继数据元素；（2）第一个数据元素没有前驱数据元素；（3）最后一个数据元素没有后继数 据元素。则称这样的数据结构为线性结构。 2.线性表定义 线性表是一种可以在任意位置进行插入和删除数据元素操作的、由 n（n ≥ 0）个相 同类型数据元素 a0, a1, a2, ., an-1 组成的线性结构。 一个有 n 个数据元素 a0, a1, a2, ., an-1 的线性表通常用符号（a0, a1, a2, ., an-1）表示，其中符号 ai（0≤i≤n-1）表示第 i 个抽象数据元素。空线性表用符号（） 表示。 2.1.2 线性表抽象数据类型 数据集合 线性表的数据元素集合可以表示为序列 a0, a1, a2, ., an-1，每个数据元素的数 据类型可以是任意的类类型。 操作集合 （1）求当前数据元素个数 size():求线性表的当前数据元素个数并由函数返回。 （2）插入数据元素 insert(i, obj)：注意 i 的合法取值 （3）删除数据元素 delete(i) ：所删除的数据元素由函数返回。删除的合法位置 （4）取数据元素 getData(i)：取线性表的第 i 个数据元素，所取的数据元素由函数返 回。 （5）线性表是否空 isEmpty()：线性表中的当前数据元素个数 size（）是否为 0。如 果 size（）为 0 函数返回 true，否则返回 false

线性表抽象数据类型的Java接口定义如下：publicinterfaceList(publicvoidinsert(inti,Objectobj)throwsException;//插入//删除public Object delete(inti)throwsException//取数据元素public Object getData(inti)throwsException;//求元素个数public intsize(;//是否空publicboolean isEmptyO:1如果一个成员函数的参数定义为根类Object，则可以使用任何类类型的实参调用该成员函数。这是因为实参到形参的参数传递过程，实际上是实参对象到形参对象引用的动态绑定过程。线性表接口List给出了任何实现线性表功能的类中必须要实现的成员函数原型，这有两方面的作用，一方面我们在进行顺序表类或单链表类的设计时，必须要根据List规范的成员函数来实现成员函数（包括函数的访问权限、成员函数名、参数类型、返回值类型）。这样就使得只要是实现了接口List的类，不管是顺序表类还是单链表类，只是函数的具体实现方法不同，所实现的功能和调用形式都是相同的：另一方面，使用顺序表类或单链表类的使用者在定义了对象后，可以根据接口List规范的成员函数原型来调用成员函数。2.2顺序表计算机有两种存储结构，一种是顺序存储结构，另一种是链式存储结构。任何需要计算机进行管理和处理的数据元素都必须首先按照某种方式存储在计算机中，一旦确定了线性表的存储结构，线性表抽象数据类型中定义的所有操作就可以具体实现了。顺序存储结构的线性表称作顺序表。下面就讨论顺序表类的设计和实现方法。2.2.1顺序表存储结构实现顺序存储结构的方法是使用数组。对于线性表，数组把线性表的数据元素存储在一块连续地址空间的内存单元中。这样线性表中，逻辑上相邻的数据元素在物理存储地址上也相邻，数据元素间的逻辑上的前驱、后继逻辑关系就表现在数据元素的存储单元的物理前后位置关系上线性表顺序存储特点：（1）逻辑上相邻的数据元素，其物理上也相邻：（2）若已知表中首元素在存储器中的位置，则其他元素存放位置亦可求出（利用数组的下标）。设首元素ao的存放地址为LOC(ao）（称为首地址），每个元素占用存储空间（地址长度）为L字节，则表中任一数据元素的存放地址为：LOC (ai+1) = LOC(ai) + LLOC (ai)=LOC(aO)+L*i例题：例如：设有一维数组M，下标的范围是0到9，每个数组元素用相邻的5个字节存储。存储器按字节编址，设存储数组元素M[0]的第一个字节的地址是98，则M[3]的第一个字节的地址是多少？解答：LOC（M[3]）=98+5X3=113

线性表抽象数据类型的 Java 接口定义如下： public interface List{ public void insert(int i, Object obj) throws Exception;//插入 public Object delete(int i ) throws Exception; //删除 public Object getData(int i ) throws Exception; //取数据元素 public int size(); //求元素个数 public boolean isEmpty(); //是否空 } 如果一个成员函数的参数定义为根类 Object，则可以使用任何类类型的实参调用该 成员函数。这是因为实参到形参的参数传递过程，实际上是实参对象到形参对象引用的动 态绑定过程。 线性表接口 List 给出了任何实现线性表功能的类中必须要实现的成员函数原型，这有 两方面的作用，一方面我们在进行顺序表类或单链表类的设计时，必须要根据 List 规范的 成员函数来实现成员函数（包括函数的访问权限、成员函数名、参数类型、返回值类型）。 这样就使得只要是实现了接口 List 的类，不管是顺序表类还是单链表类，只是函数的具体 实现方法不同，所实现的功能和调用形式都是相同的；另一方面，使用顺序表类或单链表 类的使用者在定义了对象后，可以根据接口 List 规范的成员函数原型来调用成员函数。 2.2 顺序表 计算机有两种存储结构，一种是顺序存储结构，另一种是链式存储结构。任何需要计 算机进行管理和处理的数据元素都必须首先按照某种方式存储在计算机中，一旦确定了线 性表的存储结构，线性表抽象数据类型中定义的所有操作就可以具体实现了。 顺序存储结构的线性表称作顺序表。 下面就讨论顺序表类的设计和实现方法。 2.2.1 顺序表存储结构 实现顺序存储结构的方法是使用数组。 对于线性表，数组把线性表的数据元素存储在一块连续地址空间的内存单元中。这样 线性表中，逻辑上相邻的数据元素在物理存储地址上也相邻，数据元素间的逻辑上的前驱、 后继逻辑关系就表现在数据元素的存储单元的物理前后位置关系上。 线性表顺序存储特点： (1) 逻辑上相邻的数据元素，其物理上也相邻； (2) 若已知表中首元素在存储器中的位置，则其他元素存放位置亦可求出（利用数组 的下标）。 设首元素 a0 的存放地址为 LOC(a0)（称为首地址），每个元素占用存储空间（地址长 度）为 L 字节，则表中任一数据元素的存放地址为： LOC (ai+1) = LOC(ai) + L LOC (ai) = LOC(a0) + L *i 例题： 例如：设有一维数组Ｍ，下标的范围是０到９，每个数组元素用相邻的５个字节存储。存 储器按字节编址，设存储数组元素Ｍ[０]的第一个字节的地址是 98，则Ｍ[３]的第一个字 节的地址是多少？ 解答：LOC( M[3] ) = 98 + 5 ×3 =113

2.2.2顺序表类public class SeqList implements List(final int defaultSize=10:int maxSize;int size;Object[listArray;public SeqList Ofinitiate(defaultSize):子public SeqList(int size)(initiate(size);1private void initiate(int sz) (maxSize=sz;size=0;listArray=newObject[sz];1注：确定maxSize的数值，初始化size的数值，为数组申请内存空间并使listArray等于（指向）所分配的内存空间。public void insert(int i,Object obj)throws Exceptionfif(size==maxSize) (thrownewException（“顺序表已满无法插入！”）；1if (isize)(thrownewException（“参数错误！”）：）for(int j=size;j>i;j--)listArray[j]=listArray[j-1]:listArray[i]=obj;size++;注：顺序表的插入操作，操作步骤：（1）把下标size-1至下标i中的数组元素依次后移：（2）把数据元素x插入到listArray[i]中：（3）把当前数据元素个数size加1。public Object delete(int i) throws Exceptiontif(size==0)(thrownewException(“顺序表已空无法删除！")：if (isize-1)thrownewException("参数错误！")；子Object it= listArray[i];for(int j=i;j<size-1;j++)

2.2.2 顺序表类 public class SeqList implements List{ final int defaultSize=10; int maxSize; int size; Object[] listArray; public SeqList(){ initiate(defaultSize); } public SeqList(int size){ initiate(size); } private void initiate(int sz){ maxSize=sz; size=0; listArray=new Object[sz]; } 注：确定 maxSize 的数值，初始化 size 的数值，为数组申请内存空间并使 listArray 等于（指向）所分配的内存空间。 public void insert(int i, Object obj) throws Exception{ if(size==maxSize){ throw new Exception(“顺序表已满无法插入！”)； } if (isize){ throw new Exception(“参数错误！”)； } for(int j=size;j>i;j-) listArray[j]=listArray[j-1]; listArray[i]=obj; size++; } 注：顺序表的插入操作，操作步骤： （1）把下标 size-1 至下标 i 中的数组元素依次后移； （2）把数据元素 x 插入到 listArray[i]中； （3）把当前数据元素个数 size 加 1。 public Object delete(int i) throws Exception{ if(size==0){ throw new Exception(“顺序表已空无法删除！”)； } if (isize-1){ throw new Exception(“参数错误！”)； } Object it= listArray[i]; for(int j=i;j<size-1;j++)

listArray[i]=listArray[j+1];size--, return it,1注：顺序表的删除操作，操作步骤：（1）把数据元素listArray[i]存放到临时变量x中：（2）把下标i+1至下标size-1中的数组元素依次前移；（3）把当前数据元素个数size减1。public Object getData(int i) throws Exception!if (i=size)(thrownewException(“参数错误！");3return listArray[i];1public int sizeOreturn size,1public boolean isEmptyO(return size==0;12.2.3顺序表的效率分析顺序表上的插入和删除是顺序表中时间复杂度最高的成员函数。在顺序表中插入或册除一个数据元素时，主要耗时的是循环移动数据元素部分。算法时间主要耗费在移动元素的操作上，因此计算时间复杂度的基本操作（最深层语句频度）T（n）=0（移动元素次数）。而移动元素的个数取决于插入或删除元素的位置思考：若插入在尾结点之后，则根本无需移动（特别快）；若插入在首结点之前，则表中元素全部要后移（特别慢）：应当考虑在各种位置插入（共n+1种可能）的平均移动次数才合理。推导：假定在每个元素位置上插入数据元素的可能性都一样（即概率P相同），则应当这样来计算平均执行时间：将所有位置的执行时间相加，然后取平均。若在首结点前插入，需要移动的元素最多，后移n次；若在a1后面插入，要后移n-1个元素，后移次数为n-1;.....若在an-1后面插入，要后移1个元素；若在尾结点an之后插入，则后移0个元素：所有可能的元系移动次数合计：0+1+.*+n=n（n+1）/2共有多少种插入形式?一一连头带尾有n+1种！故插入时的平均移动次数为：n(n+1)/2=（n+1）=n/2～0(n）同理可证：顺序表删除一元素的时间效率为：T (n)=(n-1)/2~0(n)顺序表支持随机读取，因此，顺序表取数据元素的时间复杂度为0（1）

listArray[j]=listArray[j+1]; size-; return it; } 注：顺序表的删除操作，操作步骤： （1）把数据元素 listArray[i]存放到临时变量 x 中； （2）把下标 i+1 至下标 size-1 中的数组元素依次前移； （3）把当前数据元素个数 size 减 1。 public Object getData(int i) throws Exception{ if (i=size){ throw new Exception(“参数错误！”)； } return listArray[i]; } public int size(){ return size; } public boolean isEmpty(){ return size==0; } } 2.2.3 顺序表的效率分析 顺序表上的插入和删除是顺序表中时间复杂度最高的成员函数。在顺序表中插入或删 除一个数据元素时，主要耗时的是循环移动数据元素部分。 算法时间主要耗费在移动元素的操作上，因此计算时间复杂度的基本操作（最深层语 句频度）T(n)= O (移动元素次数)。而移动元素的个数取决于插入或删除元素的位置. 思考：若插入在尾结点之后，则根本无需移动（特别快）； 若插入在首结点之前，则表中元素全部要后移（特别慢）； 应当考虑在各种位置插入（共 n+1 种可能）的平均移动次数才合理。 推导：假定在每个元素位置上插入数据元素的可能性都一样（即概率 P 相同），则应当这 样来计算平均执行时间：将所有位置的执行时间相加，然后取平均。 若在首结点前插入，需要移动的元素最多，后移 n 次； 若在 a1 后面插入，要后移 n-1 个元素，后移次数为 n-1; . 若在 an-1 后面插入，要后移 1 个元素； 若在尾结点 an 之后插入，则后移 0 个元素； 所有可能的元素移动次数合计： 0+1+.+n = n(n+1)/2 共有多少种插入形式?——连头带尾有 n+1 种! 故插入时的平均移动次数为：n(n+1)/2÷（n+1）＝n/2≈O(n) 同理可证：顺序表删除一元素的时间效率为: T（n）=(n-1)/2 ≈O(n) 顺序表支持随机读取，因此，顺序表取数据元素的时间复杂度为 O（1）

2.2.4顺序表应用举例例1：建立一个线性表，首先依次输入数据元素1,2.3…，10，然后删除数据元素5，最后依次显示当前线性表中的数据元素。public class SeqListTest(public static void main(String args[))(SeqList seqList =new SeqList(100):int n =10:try(for(int i=0;i<n;i++)(seqList.insert(i,newInteger(i+1));1seqList. delete(4) ;for(int i=o:i<seqList.size; i++)(System.out.print(seqList.getData(i)+"");]1catch(Exception e)(System.out.println(e.getMessageO)71例2：编写一个函数，要求把顺序表S中的数据元素序列就地逆置。所谓逆置是指把（a0，al，"，an-1）变成（an-1，"，a2，al)，就地逆置是指逆置后的数据元素仍然保存在顺序表 S 中。public void converse(SeqList s)(int mid,i;int x;mid=s.size/2:for(i=0; i<mid: i++)(x=s. listArray[i];s.listArray[i]=s.listArray[s.size-l-i];s. listArray[s.size-l-i]=x;1【本讲课程的小结】今天这一次课我们重点学习了顺序表的操作，特别是插入和删除操作是我们必须要掌握的内容。另外通过对于顺序表的分析我们应该了解顺序表的优点是支持随机存取，并且内存空间利用率高，而它的不足之处在于插入和删除数据元素需要移动大量的元素。【本讲课程的作业】1.编写一个逐个显示顺序表中所有数据元素的成员函数

2.2.4 顺序表应用举例 例 1：建立一个线性表，首先依次输入数据元素 1,2,3,.,10，然后删除数据元素 5，最后 依次显示当前线性表中的数据元素。 public class SeqListTest{ public static void main(String args[]){ SeqList seqList = new SeqList(100); int n = 10; try{ for(int i = 0; i < n; i++){ seqList.insert(i,new Integer(i+1)); } seqList.delete(4); for(int i = 0; i < seqList.size; i++){ System.out.print(seqList.getData(i)+" "); } } catch(Exception e){ System.out.println(e.getMessage()); } } } 例 2：编写一个函数，要求把顺序表 S 中的数据元素序列就地逆置。所谓逆置是指把（a0, a1,., an-1 ）变成（an-1,., a2, a1 ），就地逆置是指逆置后的数据元素仍然保存在顺 序表 S 中。 public void converse(SeqList s){ int mid,i; int x; mid=s.size/2; for(i=0; i<mid; i++){ x=s.listArray[i]; s. listArray[i]= s.listArray[s.size-1-i]; s. listArray[s.size-1-i]=x; } } 【本讲课程的小结】今天这一次课我们重点学习了顺序表的操作，特别是插入和删除操作 是我们必须要掌握的内容。另外通过对于顺序表的分析我们应该了解顺序表的优点是支持 随机存取，并且内存空间利用率高，而它的不足之处在于插入和删除数据元素需要移动大 量的元素。 【本讲课程的作业】 1. 编写一个逐个显示顺序表中所有数据元素的成员函数

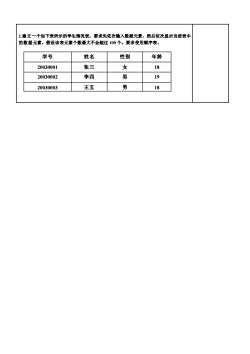
2.建立一个如下表所示的学生情况表，要求先依次输入数据元素，然后依次显示当前表中的数据元素。假设该表元素个数最大不会超过100个。要求使用顺序表。学号姓名性别年龄女张三1820030001男李四1920030002男王五1820030003

2.建立一个如下表所示的学生情况表，要求先依次输入数据元素，然后依次显示当前表中 的数据元素。假设该表元素个数最大不会超过 100 个。要求使用顺序表。 20030003 王五 男 18 20030002 李四 男 19 20030001 张三 女 18 学号 姓名 性别 年龄