《数据结构》课程教学资源（PPT课件）第五章 递归算法

第5章递归算法5.1递归的概念5.2递归算法的执行过程5.3递归算法的设计方法5.4设计举例

第5章 递归算法 5.1 递归的概念 5.2 递归算法的执行过程 5.3 递归算法的设计方法 5.4 设计举例

5.1递归的概念若一个算法直接的或间接的调用自己本身，则称这个算法是递归算法存在算法调用自己的情况：1问题定义是递推的阶乘函数的常见定义是：当n=0时2当n>0时nx(n-x...x1

5.1 递归的概念 存在算法调用自己的情况： 若一个算法直接的或间接的调用自己本身，则称这 个算法是递归算法。 阶乘函数的常见定义是： 1 问题定义是递推的

也可定义为：当n=0时21当n>0时nx(n-1)!写成函数形式，则为：当n=时当n>时n*f这种函数定义的方法是用阶乘函数自己本身定义了阶乘函数，称公式（6-3）是阶乘函数的递推定义式

也可定义为： 写成函数形式，则为： 这种函数定义的方法是用阶乘函数自己本身定义了阶乘 函数，称公式（6 – 3）是阶乘函数的递推定义式

2.问题的解法存在自调用查找17例如：折半查找算法357下标01246第一次：135417183133元素值44lowmidhighx>a[mid]023457第二次：下标16134517183133元素值444lowmidhighx<a[mid]35701246下标第三次：351718313314元素值Nlowx==a[mid]highmid

2. 问题的解法存在自调用 例如：折半查找算法 第 一 次 : 下 标 0 1 2 3 4 5 6 7 元 素 值 1 3 4 5 1 7 1 8 3 1 3 3 第 二 次 : 下 标 0 1 2 3 4 5 6 7 元 素 值 1 3 4 5 1 7 1 8 3 1 3 3 第 三 次 : 下 标 0 1 2 3 4 5 6 7 元 素 值 1 3 4 5 1 7 1 8 3 1 3 3 l o w m i d h i g h l o w m i d h i g h l o w h i g h m i d x > a [ m i d ] x < a [ m i d ] x = = a [ m i d ] 查找17

5.2递归算法的执行过程例1：阶乘的递归算法public static long fact(int n)long y;if (n< 0)(thrownewException("参数错！")1if (n == 0) return 1;else{y = fact(n-1);return n * y;77

5.2 递归算法的执行过程 例1：阶乘的递归算法 public static long fact(int n){ long y; if (n < 0){ throw new Exception("参数错！"); } if (n == 0) return 1; else { y = fact(n-1); return n * y; } }

设计一个计算3！的主函数如下,用来说明递归算法的执行过程：static void Main(stringl args)long fn;try1fn = fact(3);Console.WriteLine("fn= " + fn);1catch (Exceptione)1Console.WriteLine(e.Message);11

设计一个计算3！的主函数如下,用来说明递归算法的执行过程： static void Main(string[] args){ long fn; try { fn = fact(3); Console.WriteLine("fn = " + fn); } catch (Exception e) { Console.WriteLine(e.Message); } }

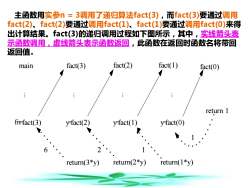
主函数用实参n=3调用了递归算法fact(3），而fact(3）要通过调用fact(2)、fact(2)要通过调用fact(1）、fact(1）要通过调用fact(0)来得出计算结果。fact(3)的递归调用过程如下图所示，其中，实线箭头表示函数调用，虚线箭头表示函数返回，此函数在返回时函数名将带回返回值。fact(1)fact(2)fact(3)mainfact(0)return1fnfact(3)yfact(2)yfact(1)yfact(0)621return(2*y)return(1*y)return(3*y)

主函数用实参n = 3调用了递归算法fact(3)，而fact(3)要通过调用 fact(2)、fact(2)要通过调用fact(1)、fact(1)要通过调用fact(0)来得 出计算结果。fact(3)的递归调用过程如下图所示，其中，实线箭头表 示函数调用，虚线箭头表示函数返回，此函数在返回时函数名将带回 返回值。 main . fn=fact(3) return(3*y) 1 6 2 1 fact(3) . y=fact(2) return(2*y) . fact(2) y=fact(1) . y=fact(0) fact(1) fact(0) return 1 return(1*y)

5.3递归算法的设计方法递归算法既是一种有效的算法设计方法，也是一种有效的分析问题的方法。递归算法求解问题的基本思想是：对于一个较为复杂的问题，把原问题分解成若干个相对简单且类同的子问题，这样较为复杂的原问题就变成了相对简单的子问题；而简单到一定程度的子问题可以直接求解：这样，原问题就可递推得到解

5.3 递归算法的设计方法 递归算法既是一种有效的算法设计方法，也是一种有效 的分析问题的方法。 递归算法求解问题的基本思想是：对于一个较为复杂的 问题，把原问题分解成若干个相对简单且类同的子问题，这 样较为复杂的原问题就变成了相对简单的子问题；而简单到 一定程度的子问题可以直接求解；这样，原问题就可递推得 到解

适宜于用递归算法求解的问题的充分必要条件是：（1）问题具有某种可借用的类同自身的子问题描述的性质（2）某一有限步的子问题（也称作本原问题）有直接的解存在。当一个问题存在上述两个基本要素时，设计该问题的递归算法的方法是：（1）把对原问题的求解表示成对子问题求解的形式。（2）设计递归出口

适宜于用递归算法求解的问题的充分必要条件是： （1）问题具有某种可借用的类同自身的子问题描述的性质 （2）某一有限步的子问题（也称作本原问题）有直接的解 存在。 当一个问题存在上述两个基本要素时，设计该问题的递归 算法的方法是： （1）把对原问题的求解表示成对子问题求解的形式。 （2）设计递归出口

例3设计模拟汉诺塔问题求解过程的算法。汉诺塔问题的描述是：设有3根标号为A，B，C的柱子，在A柱上放着n个盘子每一个都比下面的略小一点，要求把A柱上的盘子全部移到C柱上，移动的规则是：（1）一次只能移动一个盘子；（2）移动过程中大盘子不能放在小盘子上面：（3）在移动过程中盘子可以放在A，B，C的任意一个柱子上。&C234问题分析：可以用递归方法求解n个盘子的汉诺塔问题。基本思想：1个盘子的汉诺塔问题可直接移动。n个盘子的汉诺塔问题可递归表示为，首先把上边的n-1个盘子从A柱移到B柱，然后把最下边的一个盘子从A柱移到C柱，最后把移到B柱的n-1个盘子再移到C柱。4个盘子汉诺塔问题的递归求解示意图如图所示

例3 设计模拟汉诺塔问题求解过程的算法。汉诺塔问题的描 述是：设有3根标号为A，B，C的柱子，在A柱上放着n个盘子， 每一个都比下面的略小一点，要求把A柱上的盘子全部移到C 柱上，移动的规则是：（1）一次只能移动一个盘子；（2）移 动过程中大盘子不能放在小盘子上面；（3）在移动过程中盘 子可以放在A，B，C的任意一个柱子上。 问题分析：可以用递归方法求解n个盘子的汉诺塔问题。 基本思想：1个盘子的汉诺塔问题可直接移动。n个盘子的汉诺塔 问题可递归表示为，首先把上边的n-1个盘子从A柱移到B柱，然 后把最下边的一个盘子从A柱移到C柱，最后把移到B柱的n-1个 盘子再移到C柱。4个盘子汉诺塔问题的递归求解示意图如图所示。 2 1 3 4 A B C