《数据结构》课程教学资源（PPT课件）第六章 树和二叉树（6.7 树与二叉树的转换 6.8 树的遍历）

6.7哈夫曼树Huffman树Huffman编码二、卜带权路径长度最短的树Huffman树最优二叉树是通信中最经Huffman编码不等长编码典的压缩编码

6.7 哈夫曼树 一、Huffman树 二、Huffman编码 Huffman树 最优二叉树 Huffman编码 带权路径 长度最短 的树 不等长编码 是通信 中最经 典的压 缩编码

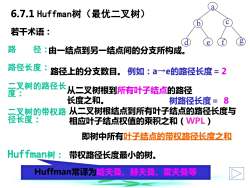
6.7.1 Huffman树寸（最优二叉树）若干术语：路径：由一结点到另一结点间的分支所构成。路径长度路径上的分支数目。例如：a一→e的路径长度=2二叉树的路径长从二叉树根到所有叶子结点的路径度：长度之和。8树路径长度=从二叉树根结点到所有叶子结点的路径长度与二叉树的带权路径长度：相应叶子结点权值的乘积之和（WPL）即树中所有吐子结点的带权路径长度之和Huffman树：带权路径长度最小的树。Huffman常译为哈夫曼、赫夫曼、霍夫曼等

6.7.1 Huffman树（最优二叉树） 路 径： 路径长度： 二叉树的路径长 度： 二叉树的带权路 径长度： Huffman树： 由一结点到另一结点间的分支所构成。 路径上的分支数目。 从二叉树根到所有叶子结点的路径 长度之和。 从二叉树根结点到所有叶子结点的路径长度与 相应叶子结点权值的乘积之和（WPL） 若干术语： d e b a c f g 即树中所有叶子结点的带权路径长度之和 带权路径长度最小的树。 例如：a→e的路径长度＝ 树路径长度＝ 2 8 Huffman常译为哈夫曼、赫夫曼、霍夫曼等

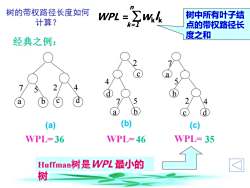
n树的带权路径长度如何Zwklk树中所有叶子结WPL =计算？k=1点的带权路径长度之和经典之例：2254./d(b)(c)(a)WPL=36WPL=35WPL=46Huffman树是WPL最小的树

树的带权路径长度如何 计算？ WPL = wk lk k=1 n a b c d 7 5 2 4 (a) c d a b 2 4 7 5 (b) b d a c 7 5 2 4 (c) 经典之例： WPL= WPL= WPL= Huffman树是WPL 最小的 树 树中所有叶子结 点的带权路径长 度之和 36 46 35

WPL最小的构造Huffman树的基本思想：权值大的结点用短路径，权值小的结点用长路径。构造Huffman树的步骤（即Huffman算法）：(1)由给定的n个权值Wi，W2，.…Wn)构造n棵二叉树的集合F={Ti,T2，T}（即森林），其中每棵二叉树T,中只有一个带权为w的根结点，其左右子树均空。（2）在F中选取两棵根结点权值最小和次小的树分别做为左右子树构造一棵新的二叉树，且让新二叉树根结点的权值等于其左右子树的根结点权值之和(3）在F中删去这两棵树，同时将新得到的二叉树加入F中重复(2）和(3），直到F只含一棵树为止。这棵树便是Huffman4树

构造Huffman树的基本思想： 权值大的结点用短路径，权值小的结点用长路径。 WPL最小的 树 构造Huffman树的步骤（即Huffman算法）： (1) 由给定的 n 个权值{ w1 , w2 , ., wn }构造n棵二叉树的集合F = { T1 , T2 , ., Tn } （即森林） ，其中每棵二叉树 Ti 中只有一个 带权为 wi 的根结点，其左右子树均空。 (2) 在F 中选取两棵根结点权值最小和次小的树分别做为左右子树 构造一棵新的二叉树，且让新二叉树根结点的权值等于其左右 子树的根结点权值之和。 (3) 在F 中删去这两棵树，同时将新得到的二叉树加入 F中。 (4) 重复(2) 和(3) , 直到 F 只含一棵树为止。这棵树便是Huffman 树

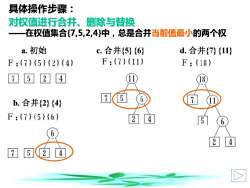
具体操作步骤：对权值进行合并、删除与替换一在权值集合(7,5,2.4)中，总是合并当前值最小的两个权a.初始c. 合并[5) (6)d. 合并(7) (11)F:(7)(11)F:(18)F:171(5)(2)(4)52485hb. 合并[2] (4)F :17)(51(6)25h124245

对权值进行合并、删除与替换 ——在权值集合{7,5,2,4}中，总是合并当前值最小的两个权 具体操作步骤： a. 初始 b. 合并{2} {4} c. 合并{5} {6} d. 合并{7} {11}

Huffman树特点：肯定没有度为1的结点；一棵有n个叶子结点的Huffman树，共有2no-1个结点（因为n=no+n,+nz=2no-1）讨论：Huffman树有什么用？例：设有4个字符d,i,a,n，出现的频度分别为7,5,2,4怎样编码才能使它们组成的报文在网络中传得最快？法1：等长编码令d=00，i=01，a=10，n=11，则:频度高的信息WPL1=2bit×(7+5+2+4) =36用短码，反之用长码，传输法2：不等长编码效率肯定高！令d=0;i=10,a=110,n=111，则WPL2=1bit×7+2bit×5+3bit×(2+4)=35

例：设有4个字符d,i,a,n，出现的频度分别为7,5,2,4， 怎样编码才能使它们组成的报文在网络中传得最快？ 法1：等长编码 令d=00，i=01，a=10，n=11，则： WPL1＝2bit×(7＋5＋2＋4）＝36 法2：不等长编码 令d=0;i=10,a=110,n=111，则： 讨论：Huffman树有什么用？ 频度高的信息 用短码，反之 用长码，传输 效率肯定高！ WPL2=1bit×7＋2bit×5+3bit×(2+4)=35 Huffman树特点：肯定没有度为1的结点；一棵有n 0个叶子结 点的Huffman树，共有2n0 -1个结点；（因为n=n0+n1+n2=2n0 -1)

6.7.2哈夫曼编码问题哈夫曼树可用于构造代码总长度最短的编码方案。具体构造方法如下：设需要编码的字符集合为{d1,d2...,dn}，各个字符在电文中出现的次数集合为{wl,w2,..,wn}，以dl,d2.,dn作为叶结点，以wl,w2,..,wn作为各叶结点的权值构造一棵二又树，规定哈夫曼树中的左分支为0，右分支为1，则从根结点到每个叶结点所经过的分支对应的0和1组成的序列便为该结点对应字符的编码。这样的代码总长度最短的不等长编码称之为哈夫曼编码。明确：要实现哈夫曼编码，就要先构造哈夫曼树

6.7.2 哈夫曼编码问题 哈夫曼树可用于构造代码总长度最短的编码方案。具体 构造方法如下： 设需要编码的字符集合为{d1,d2,.,dn}，各个字符在电 文中出现的次数集合为{w1,w2,.,wn}，以d1,d2,.,dn作为叶 结点，以w1,w2,.,wn作为各叶结点的权值构造一棵二叉树， 规定哈夫曼树中的左分支为0，右分支为1，则从根结点到每 个叶结点所经过的分支对应的0和1组成的序列便为该结点对 应字符的编码。这样的代码总长度最短的不等长编码称之为 哈夫曼编码。 明确：要实现哈夫曼编码，就要先构造哈夫曼树

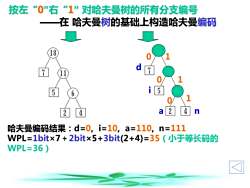
按左“0”右“1”对哈夫曼树的所有分支编号一一在哈夫曼树的基础上构造哈夫曼编码心5h24哈夫曼编码结果：d=0，i=10，a=110，n=111WPL=1bit×7+2bit×5+3bit（2+4）=35（小于等长码的WPL=36）

按左“0”右“1” 对哈夫曼树的所有分支编号 d a i n 1 1 0 1 0 0 哈夫曼编码结果：d=0, i=10, a=110, n=111 WPL=1bit×7＋2bit×5+3bit(2+4)=35（小于等长码的 WPL=36） ——在 哈夫曼树的基础上构造哈夫曼编码

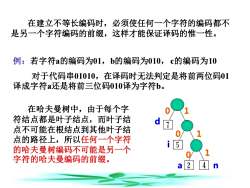
在建立不等长编码时，必须使任何一个字符的编码都不是另一个字符编码的前缀，这样才能保证译码的惟一性。例：若字符a的编码为01，b的编码为010，c的编码为10对于代码串01010，在译码时无法判定是将前两位码01译成字符a还是将前三位码010译为字符b。在哈夫曼树中，由于每个字配符结点都是叶子结点，而叶子结d7点不可能在根结点到其他叶子结点的路径上，所以任何一个字符的哈夫曼树编码不可能是另一个字符的哈夫曼编码的前缀。7

在建立不等长编码时，必须使任何一个字符的编码都不 是另一个字符编码的前缀，这样才能保证译码的惟一性。 例：若字符a的编码为01，b的编码为010，c的编码为10 对于代码串01010，在译码时无法判定是将前两位码01 译成字符a还是将前三位码010译为字符b。 在哈夫曼树中，由于每个字 符结点都是叶子结点，而叶子结 点不可能在根结点到其他叶子结 点的路径上，所以任何一个字符 的哈夫曼树编码不可能是另一个 字符的哈夫曼编码的前缀。 d a i n 1 1 0 1 0 0

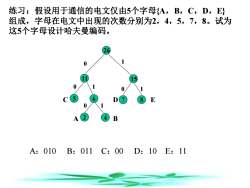
练习：假设用于通信的电文仅由5个字母A，B，C，D，E组成，字母在电文中出现的次数分别为2，4，5，7，8。试为这5个字母设计哈夫曼编码。E1BA:010B: 011C:00D:10E: 11

练习：假设用于通信的电文仅由5个字母{A，B，C，D，E} 组成，字母在电文中出现的次数分别为2，4，5，7，8。试为 这5个字母设计哈夫曼编码。 2 4 5 6 11 7 8 15 26 0 1 0 0 0 1 1 1 A B C D E A：010 B：011 C：00 D：10 E：11