中国农业大学：《畜牧生物统计与实验设计》课程教学课件（PPT讲稿）第三章 随机变量与概论分布

第三章 随机变量与概率分布 ⚫随机变量及其种类 ⚫概率分布 ⚫正态分布 ⚫二项分布

第三章 随机变量与概率分布 ⚫随机变量及其种类 ⚫概率分布 ⚫正态分布 ⚫二项分布

随机变量及其种类 ⚫随机变量（random variable） ➢在一定范围内随机取值的变量 ➢以一定的概率分布取值的变量 ⚫分类 ➢离散型(discrete)随机变量：只取有限个可能值（通 常为整数） • 例：发病个体数，产仔数 ➢连续型(continuous)随机变量：在一定范围内可取 无限个可能值（实数） • 例：产奶量，体长，日增重

随机变量及其种类 ⚫随机变量（random variable） ➢在一定范围内随机取值的变量 ➢以一定的概率分布取值的变量 ⚫分类 ➢离散型(discrete)随机变量：只取有限个可能值（通 常为整数） • 例：发病个体数，产仔数 ➢连续型(continuous)随机变量：在一定范围内可取 无限个可能值（实数） • 例：产奶量，体长，日增重

概率分布 ⚫概率函数(probability function) ➢随机变量取某一特定值的概率函数（离散型 随机变量） ⚫ 概率密度函数(probability density function) ➢随机变量取某一特定值的密度函数（连续型 随机变量） ⚫ 概率分布函数(probability distribution function) ➢随机变量取值小于或等于某特定值的概率

概率分布 ⚫概率函数(probability function) ➢随机变量取某一特定值的概率函数（离散型 随机变量） ⚫ 概率密度函数(probability density function) ➢随机变量取某一特定值的密度函数（连续型 随机变量） ⚫ 概率分布函数(probability distribution function) ➢随机变量取值小于或等于某特定值的概率

离散型随机变量的概率分布 ⚫概率函数 f (x) = P(X = x) X ：随机变量，x：该随机变量的某一可能取值   = x f x f x 所有 ( ) 0 , ( ) 1 ⚫概率分布函数   =  = y x F(x) P(X x) f ( y)

离散型随机变量的概率分布 ⚫概率函数 f (x) = P(X = x) X ：随机变量，x：该随机变量的某一可能取值   = x f x f x 所有 ( ) 0 , ( ) 1 ⚫概率分布函数   =  = y x F(x) P(X x) f ( y)

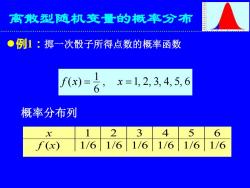
离散型随机变量的概率分布 ⚫例1：掷一次骰子所得点数的概率函数 , 1, 2, 3, 4, 5, 6 6 1 f (x) = x = x 1 2 3 4 5 6 f (x) 1/6 1/6 1/6 1/6 1/6 1/6 概率分布列

离散型随机变量的概率分布 ⚫例1：掷一次骰子所得点数的概率函数 , 1, 2, 3, 4, 5, 6 6 1 f (x) = x = x 1 2 3 4 5 6 f (x) 1/6 1/6 1/6 1/6 1/6 1/6 概率分布列

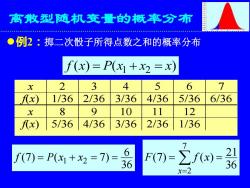
离散型随机变量的概率分布 ⚫例2：掷二次骰子所得点数之和的概率分布 x 2 3 4 5 6 7 f(x) 1/36 2/36 3/36 4/36 5/36 6/36 x 8 9 10 11 12 f(x) 5/36 4/36 3/36 2/36 1/36 36 21 (7) ( ) 7 2 =  = x= F f x 36 6 (7) ( 7) f = P x1 + x2 = = ( ) ( ) 1 2 f x = P x + x = x

离散型随机变量的概率分布 ⚫例2：掷二次骰子所得点数之和的概率分布 x 2 3 4 5 6 7 f(x) 1/36 2/36 3/36 4/36 5/36 6/36 x 8 9 10 11 12 f(x) 5/36 4/36 3/36 2/36 1/36 36 21 (7) ( ) 7 2 =  = x= F f x 36 6 (7) ( 7) f = P x1 + x2 = = ( ) ( ) 1 2 f x = P x + x = x

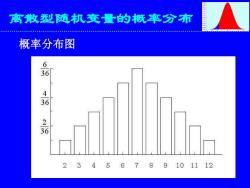
离散型随机变量的概率分布 概率分布图

离散型随机变量的概率分布 概率分布图

离散型随机变量的概率分布 ⚫随机变量的期望(expectation) - 总体平均 数 = ( ) = ( ) i i  E X x f x 对于例1： 3.5 (1 2 3 4 5 6) 6 1 6 1 ( ) =  = E X = xi = + + + + +

离散型随机变量的概率分布 ⚫随机变量的期望(expectation) - 总体平均 数 = ( ) = ( ) i i  E X x f x 对于例1： 3.5 (1 2 3 4 5 6) 6 1 6 1 ( ) =  = E X = xi = + + + + +

离散型随机变量的概率分布 ⚫期望的性质 E(a) = a E(X +Y) = E(X ) + E(Y) E(aX ) = aE(X ) (a是常量) E(XY) = E(X )E(Y) 1. 2. 3. 4. （当X和Y彼此独立）

离散型随机变量的概率分布 ⚫期望的性质 E(a) = a E(X +Y) = E(X ) + E(Y) E(aX ) = aE(X ) (a是常量) E(XY) = E(X )E(Y) 1. 2. 3. 4. （当X和Y彼此独立）

离散型随机变量的概率分布 [ ( )] = ( ) ( ) i i E H X H x f x ⚫随机变量的函数的期望 设H(X)是随机变量X的某个函数 ( ) =  ( ) 2 2 i i 例： E X x f x 2 H(X) = X 对于例1： 15.167 (1 2 3 4 5 6 ) 6 1 6 1 ( ) 2 2 2 2 2 2 2 2 = E X = xi = + + + + +

离散型随机变量的概率分布 [ ( )] = ( ) ( ) i i E H X H x f x ⚫随机变量的函数的期望 设H(X)是随机变量X的某个函数 ( ) =  ( ) 2 2 i i 例： E X x f x 2 H(X) = X 对于例1： 15.167 (1 2 3 4 5 6 ) 6 1 6 1 ( ) 2 2 2 2 2 2 2 2 = E X = xi = + + + + +