南京大学：《计算机问题求解》课程教学资源（PPT课件讲稿）什么样的推理是正确的

问题求解 论题1-2：什么样的推理是正确的？ Logic--The discipline that deals with the methods of reasoning majun@nju.edu.cn 2017.10.12

单击此处编辑母版标题样式 majun@nju.edu.cn 2017.10.12 Logic--The discipline that deals with the methods of reasoning 问题求解 论题1-2：什么样的推理是正确的？

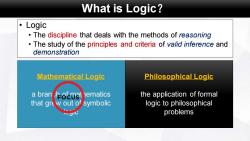
What is Logic? Logic The discipline that deals with the methods of reasoning The study of the principles and criteria of valid inference and demonstration Mathematical Logic Philosophical Logic a bran h-8mat ematics the application of formal that gre w out of symbolic logic to philosophical problems

What is Logic？ • Logic • The discipline that deals with the methods of reasoning • The study of the principles and criteria of valid inference and demonstration Mathematical Logic a branch of mathematics that grew out of symbolic logic Philosophical Logic the application of formal logic to philosophical problems

An Example:Home Town We know that Bill,Jim and Sam are from Boston,Chicago and Detroit,respectively. Each of following sentence is half right and half wrong: Bill is from Boston,and Jim is from Chicago. Sam is from Boston,and Bill is from Chicago. Jim is from Boston,and Bill is from Detroit. Tell the truth about their home towns

• We know that Bill, Jim and Sam are from Boston, Chicago and Detroit, respectively. • Each of following sentence is half right and half wrong: • Bill is from Boston, and Jim is from Chicago. • Sam is from Boston, and Bill is from Chicago. • Jim is from Boston, and Bill is from Detroit. • Tell the truth about their home towns. An Example: Home Town

How to solve it? Understanding the problem! Bill,Jim and Sam are from Boston,Chicago and Detroit,respectively Each of following sentence is half right and half wrong: Bill is from Boston,and Jim is from Chicago. Guessing Bill is from Boston,if and only if Jim is NOT from Chicago. and Jim is from Chicago,if and only if Bill is NOT from Boston. Reasoning Sam is from Boston,and Bill is from Chicago. Sam is from Boston,if and only if Bill is NOT from Chicago. Bill is from Chicago,if and only if Sam is NOT from Boston. Jim is from Boston,and Bill is from Detroit. Jim is from Boston,if and only if Bill is NOT from Detroit. Bill is from Detroit,if and only if Jim is NOT from Boston

How to solve it? • Bill, Jim and Sam are from Boston, Chicago and Detroit, respectively • Each of following sentence is half right and half wrong: • Bill is from Boston, and Jim is from Chicago. • Bill is from Boston, if and only if Jim is NOT from Chicago. • Jim is from Chicago, if and only if Bill is NOT from Boston. • Sam is from Boston, and Bill is from Chicago. • Sam is from Boston, if and only if Bill is NOT from Chicago. • Bill is from Chicago, if and only if Sam is NOT from Boston. • Jim is from Boston, and Bill is from Detroit. • Jim is from Boston, if and only if Bill is NOT from Detroit. • Bill is from Detroit, if and only if Jim is NOT from Boston. Guessing and Reasoning Understanding the problem!

One Possible Reasoning ·Guessing that“Bill is from Boston", Bill,Jim and Sam are from then Boston,Chicago and Detroit, respectively Jim is NOT from Chicago ·Jim is NOT from Boston ·Bill is from Detroit CONFLICT Bill is from Boston,if and only if Jim is NOT from Chicago. Sam is from Boston,if and only So the guessing is wrong,and if Bill is NOT from Chicago. ·Jim is from Chicago ·Bill is from Detroit Jim is from Boston,if and only ·Sam is from Boston if Bill is NOT from Detroit

One Possible Reasoning • Guessing that “Bill is from Boston”, then • Jim is NOT from Chicago • Jim is NOT from Boston • Bill is from Detroit • So the guessing is wrong, and • Jim is from Chicago • Bill is from Detroit • Sam is from Boston • Bill, Jim and Sam are from Boston, Chicago and Detroit, respectively • Bill is from Boston, if and only if Jim is NOT from Chicago. • Sam is from Boston, if and only if Bill is NOT from Chicago. • Jim is from Boston, if and only if Bill is NOT from Detroit

Question ONE There are some principles and rules guiding the reasoning process. Can we specify them in a They are mathematical independent with way? the facts/contents we are reasoning about

Question ONE Can we specify them in a mathematical way? There are some principles and rules guiding the reasoning process. They are independent with the facts/contents we are reasoning about

Formalization 勉 WHY Precise Effective Correct Description Reasoning Proving do we need How to How to carry out What is a correct unambiguously reasoning? proof? formalization? specify a statement

Formalization WHY do we need formalization? How to unambiguously specify a statement. Precise Description How to carry out reasoning? Effective Reasoning What is a correct proof? Correct Proving

Formalization Proposition Proposition Variable Logic Connectives Fundamental Logic Logic Formulas Logical Equivalence Elements Predicate Inference Quantifier

Formalization Fundamental Logic Elements ► Proposition & Proposition Variable ► Logic Connectives ► Logic Formulas ► Logical Equivalence ► Predicate & Quantifier ► Inference

Proposition(命题) A proposition/statement is a sentence that is true or false (might be unknown),but not both My salary of this month is greater than that of last month. Today is Tuesday,and it is raining. Can you speak English? 3-x=5 Every even integer greater than 2 can be expressed as the sum of two primes "What I'm talking now is fake." paradox

is a sentence that is true or false (might be unknown), but not both Proposition（命题） A proposition/statement My salary of this month is greater than that of last month. Today is Tuesday, and it is raining. Can you speak English? 3-x=5 Every even integer greater than 2 can be expressed as the sum of two primes “What I’m talking now is fake.” paradox

Proposition Variable(命题变元) Usually,we use lower case letters to denote proposition variables (e.g.,p,q,r) ·p:Today is Friday ·q:2+2=4 ·r:Bill is from Boston ·The range of a proposition variable:{T,月 p:Today is Friday(p=F) ·q:2+2=4(q=T) r:Bill is from Boston (r=F)

Proposition Variable（命题变元） • Usually, we use lower case letters to denote proposition variables (e.g., p, q, r) • p : Today is Friday • q : 2+2=4 • r : Bill is from Boston • The range of a proposition variable: {T, F} • p: Today is Friday (p=F) • q: 2+2=4 (q =T) • r: Bill is from Boston (r=F)