南京大学：《计算机问题求解》课程教学资源（PPT课件讲稿）置换群与拉格朗日定理（OLD）

计算机问题求解一论题3-17 -置换群与拉格朗日定理 2017年3月6日

计算机问题求解 – 论题3-17 - 置换群与拉格朗日定理 2017年3月6日

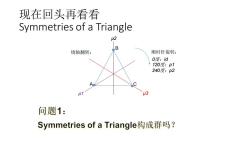
现在回头再看看 Symmetries of a Triangle u2 B 绕轴翻转： 顺时针旋转： 0度：id 120度：p1 240度：p2 1 u3 问题1： Symmetries of a Triangle构成群吗？

现在回头再看看 Symmetries of a Triangle A B C 0度：id 120度：ρ1 240度：ρ2 μ2 μ1 μ3 绕轴翻转： 顺时针旋转：

问题2： 为什么一个有限集合上所有一 一对应的函数一定能构成一个 群？

置换复合运算示例 It is very easy to compute products of cycles.Suppose that o=(1352)andT=(256).μ=(1634) 0儿三？

置换复合运算示例 ？ ？

关于置换的轮换表示 Example 6.Let 任意Sn置换 23456 6 4315 总是可以表示 1 234 5 6 为不相关的轮 3 2 156 换的复合！ Using cycle notation,we can write σ=(1624) 任意不相关的 T=(13)(456) 轮换的复合是 σT=(136)(245) T0=(143)(256). 可交换的！ 问题3：你能从上述两个结论的证明过程中总结出关于置换相关命 题的某种证明方法吗？

关于置换的轮换表示 任意Sn置换 总是可以表示 为不相关的轮 换的复合！ 任意不相关的 轮换的复合是 可交换的！ 问题3：你能从上述两个结论的证明过程中总结出关于置换相关命 题的某种证明方法吗？

问题4.1：你能一眼看出这个结论吗？ Since (a1,a2,.,an）=(a1an)(a1an-1）…(a1a3)(a1a2） any cycle can be written as the product of transpositions 问题4.2：上述结论如何导致这个命题的？ Proposition 5.4 Any permutation of a finite set containing at least two elements can be written as the product of transpositions. 问题5：你能很快地给出一个置换的逆是什么吗？

问题4.1:你能一眼看出这个结论吗？ 问题4.2:上述结论如何导致这个命题的？ 问题5：你能很快地给出一个置换的逆是什么吗？

副扑克牌，如果洗牌时每次交换两张牌，洗 牌n次后，恰好还原了。请问n有可能是137吗？ Lemma 5.5 If the identity is written as the product ofr transpositions, id=T1T2…Tr, then r is an even number. 以上述定理为基础，我们很容易证明：一个置换的奇偶性是确定的

一副扑克牌，如果洗牌时每次交换两张牌，洗 牌n次后，恰好还原了。请问n有可能是137吗？ 以上述定理为基础，我们很容易证明：一个置换的奇偶性是确定的

Dose this surprise you? Example 8.The group A4 is the subgroup of S4 consisting of even permu- tations.There are twelve elements in A4:

Dose this surprise you?

子群的陪集 Let G be a group and H a subgroup of G.Define a left coset of H with representative g EG to be the set gH={gh hEH Right cosets can be defined similarly by Hg={hg:hEH. Example 1.Let H be the subgroup of Z6 consisting of the elements 0 and 3.The cosets are 0+H=3+H={0,3} 1+H=4+H={1,4 2+H=5+H={2,5}

子群的陪集

子群的陪集 问题6.1： H和gH是否肯定“一样大”？ 问题6.2g 请gH中会不会有相同元素？有相同元素 意味着什么？ 问题6.3： 什么样的元素，它们的陪集是相同的？

子群的陪集 问题6.3： 什么样的元素，它们的陪集是相同的？