南京大学：《计算机问题求解》课程教学资源（PPT课件讲稿）串匹配

计算机问题求解-论题4-5 。串匹配 2019年3月27日

计算机问题求解 – 论题4-5 - 串匹配 2019年3月27日

问题1： 什么是string-matching problem,直观上？形式上？

string-matching problem

几乎每天都在用。。 Introduction to Algorithms,Third Edition 1007/1313 Knuth-Morris-Pratt 1/2 Tigure 32.2 The strmg-matehing aigonmms m ts cnaprer and men preprocessig and matcmng times. Except for the naive brute-force algorithm.which we review in Section 32.1. each string-matching algorithm in this chapter performs some preprocessing based on the pattern and then finds all valid shifts;we call this latter phase"matching." Figure 32.2 shows the preprocessing and matching times for each of the algorithms in this chapter.The total running time of each algorithm is the sum of the prepro- cessing and matching times.Section 32.2 presents an interesting string-matching algorithm.due to Rabin and Karp.Although the ((n-m +1)m)worst-case running time of this algorithm is no better than that of the naive method,it works much better on average and in practice.It also generalizes nicely to other pattern- matching problems.Section 32.3 then describes a string-matching algorithm that begins by constructing a finite automaton specifically designed to search for occur- rences of the given pattern P in a text.This algorithm takes O(m preprocess- ing time,but only (n)matching time.Section 32.4 presents the similar,but much cleverer.Knuth-Morris-Pratt (or KMP)algorithm:it has the same (n)matching time,and it reduces the preprocessing time to only (m). 出 Notation and terminology We denote by E*(read"sigma-star")the set of all finite-length strings formed using characters from the alphabet In this chapter,we consider only finite- length strings.The zero-length empty string,denoted 8,also belongs to 'The

几乎每天都在用

text T a b c ab a a b a b a 5=3 a a we say that pattern P occurs with shift s in text T (or,equivalently,that pattern P occurs beginning at position s+1 in text T)if 0≤s≤n-m and T5+l.s+m=P[l.m(that is,.ifT5+j】=P[Ujl,for 1 j<m).If P occurs with shift s in T,then we call s a valid shift;otherwise, we call s an invalid shift.The string-matching problem is the problem of finding all valid shifts with which a given pattern P occurs in a given text T

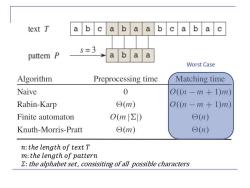
text T a b a b a a b a b a 5=3 pattern P b a a Worst Case Algorithm Preprocessing time Matching time Naive 0 O((n-m+1)m) Rabin-Karp ⊙(m) O(n-m+1)m)） Finite automaton O(m∑) ⊙(n) Knuth-Morris-Pratt ⊙(m) Θ(n) n:the length of text T m:the length of pattern the alphabet set,consisiting ofall possible characters

𝑛:𝑡ℎ𝑒 𝑙𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 𝑡𝑒𝑥𝑡 𝑇 𝑚:𝑡ℎ𝑒 𝑙𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 𝑝𝑎𝑡𝑡𝑒𝑟𝑛 𝛴:the alphabet set , consisiting of all possible characters Worst Case

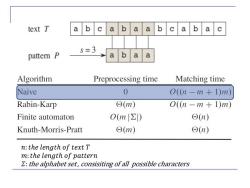
text T a b a b a a b a b a =3 pattern P b a a Algorithm Preprocessing time Matching time Naive 0 O(n-m+1)m) Rabin-Karp ⊙(m) O(n-m+1)m) Finite automaton O(1m∑) Θ(n) Knuth-Morris-Pratt Θ(1m) Θ(n) n:the length of text T m:the length of pattern the alphabet set,consisiting ofall possible characters

𝑛:𝑡ℎ𝑒 𝑙𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 𝑡𝑒𝑥𝑡 𝑇 𝑚:𝑡ℎ𝑒 𝑙𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 𝑝𝑎𝑡𝑡𝑒𝑟𝑛 𝛴:the alphabet set , consisiting of all possible characters

最容易想到的算法 a a a b a a a b a a a b a a a b s=0 5=3 a a b b a a b NAIVE-STRING-MATCHER(T.P) 问题2： 1 n T.length 2 m =P.length 最坏情况下复杂度？ 3 fors 0to n-m 0(n-m+1)m) 4 if P[1..ml==T[s +1..s+ml 5 print"Pattern occurs with shift"s 问题3：什么时候出现最坏情况？

最容易想到的算法 𝑶 𝒏 − 𝒎 + 𝟏 𝒎

问题4：你能否说说naive.算法有什么问 题，为什么有可能改进？ a a b a a a a b S=0 S=3 a a b a a b NAIVE-STRING-MATCHER(T,P) 逐位单字符比较 1 n T.length The naive string-matcher is 2 m P.length inefficient because it entirely 3 fors 0to n-m ignores information gained if P[1..m ==Ts +1..s+m about the text for one value print“Pattern occurs with shift”s of s when it considers other values of s

The naive string-matcher is inefficient because it entirely ignores information gained about the text for one value of s when it considers other values of s

text T a b a b a a b a b a =3 pattern P b a a Algorithm Preprocessing time Matching time Naive 0 O(n-m+1)m) Rabin-Karp ⊙(m) O(n-m+1)m) Finite automaton O(m∑) ⊙(n) Knuth-Morris-Pratt Θ(1m) ©(n) n:the length of text T m:the length of pattern the alphabet set,consisiting ofall possible characters

𝑛:𝑡ℎ𝑒 𝑙𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 𝑡𝑒𝑥𝑡 𝑇 𝑚:𝑡ℎ𝑒 𝑙𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 𝑝𝑎𝑡𝑡𝑒𝑟𝑛 𝛴:the alphabet set , consisiting of all possible characters

问题5： Rabin-Karp算法的基本思想 是什么？ For expository purposes,let us assume that∑={0,1,2，.，9}，so that each character is a decimal digit.(In the general case,we can assume that each charac- ter is a digit in radix-d notation,where d=We can then view a string ofk consecutive characters as representing a length-k decimal number.The character string 31415 thus corresponds to the decimal number 31,415

问题5： Rabin-Karp算法的基本思想 是什么？