南京大学：《计算机问题求解》课程教学资源（PPT课件讲稿）最大流算法

计算机问题求解-论题3-13 ·最大流算法 2018年12月4日

计算机问题求解 – 论题3-13 - 最大流算法 2018年12月4日

Lucky Puck Company's Trucking Problem Lucky:公司生产冰球，其工厂在温哥华，仓库在温尼泊。公司 委托物流公司运输。物流公司经营固定线路网，可能经过多 个中间城市。分配给Lucky公司的任意两个城市间的最大运输 量是固定的。如果Lucky公司是按运输量确定生产量，它如何 计划它每天最大产量？ 问题1： 如何建立解决这个问题的模型？

Lucky Puck Company’s Trucking Problem Lucky公司生产冰球，其工厂在温哥华，仓库在温尼泊。公司 委托物流公司运输。物流公司经营固定线路网，可能经过多 个中间城市。分配给Lucky公司的任意两个城市间的最大运输 量是固定的。如果Lucky公司是按运输量确定生产量，它如何 计划它每天最大产量？

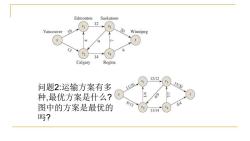
Edmonton Saskatoon 12 Vancouver 16 30 Winnipeg /3 V 14 Calgary Regina 12/12 问题2：运输方案有多 11/16 15/20 种，最优方案是什么？ 4/9 图中的方案是最优的 8/13 4/4 VA 11/14 吗？

问题2:运输方案有多 种,最优方案是什么? 图中的方案是最优的 吗?

问题3： 如果工厂与仓库都不止一 个，该怎么办？

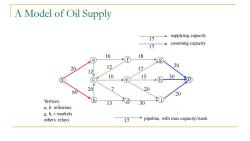
A Model of Oil Supply 17 supplying capacity cosuming capacity 17 16 18 a 20 20 12 12 17 10 15 30 >(e h 60 20 20 20 Vertices: b 13 30 a,b:refineries g,h,i:markets others:relays 17 pipeline,with max capacity/week

A Model of Oil Supply a b c d f e g h i S 20 60 D 20 30 20 16 18 12 17 10 7 13 30 20 15 Vertices: a, b: refineries g, h, i: markets others: relays 17 pipeline, with max capacity/week 17 17 supplying capacity cosuming capacity 12 20

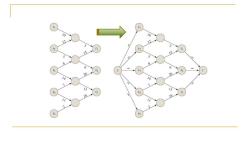
1 10 10 2 2 3 3 t 5 5 6 00 6 00 S3 12 s3 20 20 14 14 7 6 7 3 5 13 13 18 18 11 2 2 雪 5

严格的数学模型 We are now ready to define flows more formally.Let G =(V.E)be a flow network with a capacity function c.Let s be the source of the network,and let t be the sink.A flow in G is a real-valued function f:Vx V-R that satisfies the following two properties: Capacity constraint: Flow conservation:For all ue V-fs.t,we require When (u,v)E,there can be no flow from u to v,and f(u,v)=0

严格的数学模型

问题4： 什么叫一个flow的*value即？ IfI=∑fs,)-∑fw,) ve V 什么是最大流问题？

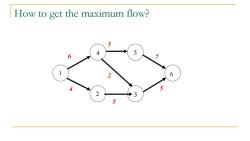
How to get the maximum flow? 5 4 5 6 2 6 4 5 2 3 5

How to get the maximum flow? 6 4 5 2 3 1 5 5 4 7 5 6 2

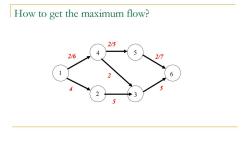
How to get the maximum flow? 2/5 5 2/6 4 2/7 2 6 4 5 2 3 5

How to get the maximum flow? 6 4 5 2 3 1 5 5 4 2/7 2/5 2/6 2