石河子大学：《运筹学》课程教学资源（实验指导）线性规划问题的WinQSB建模求解

(一)线性规划问题的WinQSB建模求解 说明 √用WinQSB软件求解LP问题不必化为标准形 √对于有界变量可以不转化只要修改系统变量类型即可： √对于不等式约束可以在输入数据时直接输入不等式。 实验目的：学握在WinQSB中建立线性规划模型和求解的方法 实验内容： 求解下列线性规划问题： min:=+2x2+3x [-2x1+x2+x≤9 -3x+x2+2x324 3x1-2x2-3x3=-6 x≥0，x2≥0，x取值无约束 实验步骤 l、运行“Linear and integer programming”,出现图1所示界面 Linear and Integer Programsing Eile Help 图1 2、运行file菜单下的new problem命令，出现图2所示界面。 LP-ILP Problea Specification 问题名称 Problem Title: 决策变量个数 约束条件个数 Objective Criterion Defult Variable Type 非负连续 (不含变量约束) Nonnegative continuous 变量 0非负整数变 目标函数类型 Entry Format 08nay0,0-1整数变量 数据类型 0 ne不定 输入数据格式：选择 OK Cancel He Spreadsheet Matrix From 图2

（一）线性规划问题的 WinQSB 建模求解 说明：  用 WinQSB 软件求解 LP 问题不必化为标准形；  对于有界变量可以不转化只要修改系统变量类型即可；  对于不等式约束可以在输入数据时直接输入不等式。 实验目的:掌握在 WinQSB 中建立线性规划模型和求解的方法 实验内容: 求解下列线性规划问题： 实验步骤 1、运行“Linear and integer programming”，出现图 1 所示界面 2、运行 file 菜单下的 new problem 命令，出现图 2 所示界面。 图 2 问题名称 决策变量个数 约束条件个数 （不含变量约束） 目标函数类型 数据类型 输入数据格式：选择 Spreadsheet Matrix From 非负连续 变量 非负整数变量 0-1 整数变量 不定义 图 1                         1 2 3取值无约束 1 2 3 1 2 3 1 2 3 1 2 3 0, 0, 3 2 3 6 3 2 4 2 9 min 2 3 x x x x x x x x x x x x z x x x

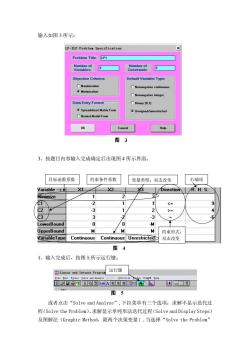
输入如图3所示 LP-ILP Probles Specification Problem Title:LP1 Number of 3 Objective Criterion Default Variable Type Nonnegative continuou inimtatio Data Entry Format Binary [0.1] Unsigned/untestricted Normal Model Form OK Cancel Help 图3 3、按题目内容输入完成确定后出现图4所示界面。 目标函数系数 约束条件系数 变量类型：双击改变 右端项 Variable-> X1 X2 3 DirectionR.H.S. inimize C2 -3 》= C3 JpperBound M 约束形式： ariableType Continuous Continuous Unrestricted 双击改变 图4 4、输入完成后，按图5所示运行键。 运行键 图5 或者点击“Solve and Analyze”,下拉菜单有三个选项：求解不显示迭代过 程(Solve the Problem)、求解显示单纯形法迭代过程(Solve and Display Steps》 及图解法(Graphic Method,.限两个决策变量).当选择“Solve the Problem

输入如图 3 所示： 3、按题目内容输入完成确定后出现图 4 所示界面。 4、修改变量名和约束名. 系统默认变量名为 x1,x2,.,xn,约束名为 c1,c2,.,cm。 可以通过点击“Edit”后，用下拉菜单中四个选项来修改标题名（Problem Name）、变量名（Variable Name）、约束名（Constraint Name）和目标函数准则 （max 和 min）。 4、输入完成后，按图 5 所示运行键。 或者点击“Solve and Analyze”,下拉菜单有三个选项：求解不显示迭代过 程（Solve the Problem）、求解显示单纯形法迭代过程（Solve and Display Steps） 及图解法（Graphic Method，限两个决策变量）.当选择“Solve the Problem” 图 4 目标函数系数 约束条件系数 变量类型：双击改变 约束形式： 双击改变 右端项 图 5 运行键 图 3

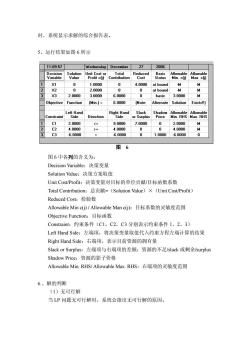
时，系统显示求解的综合报告表。 5、运行结果如图6所示 11:0957 Wednesday December 27 2006 1X1 0 1.0000 0 4.0000 at bound M M 2 X2 2.0000 0 at bound M M 3X3 2.0000 3.00006.0000 0 basic 3.0000 Objective Function (Min.]=6.0000 (Note:Alternate Solution Existsll] Constraint Direction Min.RHS Max.RHS 2.0000 9.00007.00000 2.0000 M C24.0000 》= 4.0000 0 4.0000 3 C3-6.0000 6.00000 1.0000-6.0000 0 图6 图6中各列的含义为： Decision Variable:决策变量 Solution Value:决策方案取值 Unit Cost/Profit:决策变量对目标的单位贡献/目标函数系数 Total Contribution:总贡献=(Solution Value)X(Unit Cost//Profit) Reduced Cost:.检验数 Allowable Min c()j/Allowable Man c(j):目标系数的灵敏度范围 Objective Function:目标函数 Constraint::约束条件(C1,C2,C3分别表示约束条件1、2、3) Left Hand Side:左端项，将决策变量取值代入约束方程左端计算的结果 Right Hand Side:右端项，表示目前资源的拥有量 Slack or Surplus:左端项与右端项的差额：资源的不足//slack或剩余/surplus Shadow Price:资源的影子价格 Allowable Min.RHS/Allowable Max.RHS:右端项的灵敏度范围 6.、解的判断 (1)无可行解 当LP问题无可行解时，系统会指出无可行解的原因

时，系统显示求解的综合报告表。 5、运行结果如图 6 所示 图 6 中各列的含义为： Decision Variable：决策变量 Solution Value：决策方案取值 Unit Cost/Profit：决策变量对目标的单位贡献/目标函数系数 Total Contribution：总贡献=（Solution Value）×（Unit Cost/Profit） Reduced Cost：检验数 Allowable Min c(j) / Allowable Man c(j)：目标系数的灵敏度范围 Objective Function：目标函数 Constraint：约束条件（C1，C2，C3 分别表示约束条件 1、2、3） Left Hand Side：左端项，将决策变量取值代入约束方程左端计算的结果 Right Hand Side：右端项，表示目前资源的拥有量 Slack or Surplus：左端项与右端项的差额：资源的不足/slack 或剩余/surplus Shadow Price：资源的影子价格 Allowable Min. RHS/ Allowable Max. RHS：右端项的灵敏度范围 6.、解的判断 （1）无可行解 当 LP 问题无可行解时，系统会指出无可行解的原因。 图 6

Linear and Integer Programming 销定 (2)无穷多最优解 c 1.4286 6.0000 8.5714 basic ,266.000049.0000 X2 0 5.0000 0 at bound M43.8571 3 20.0000 1.0000 20.0000 basic 51429 98.5714 7.00 690.0000 at bound M 7.0000 Objective Function Wa▣ -661.4285 Alternate Solution Existsl!] (3)无界解 Linear and Integer Progranming 确定 作业练习： 1.用WinQSB求解课本P47页1.1（分析四种解的不同处理显示情况）

（2）无穷多最优解 （3）无界解 作业练习： 1. 用 WinQSB求解课本 P47页 1.1（分析四种解的不同处理显示情况）