山东第一医科大学（泰山医学院）：《高等数学》课程教学课件（打印版）第八章 空间解析几何与向量代数

第一节向量及其线性运算 一、空间直角坐标系 二、向量概念 三、向量的线性运算 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影 2012-3-29 泰山医学院信息工程学院高等数学教研室 1

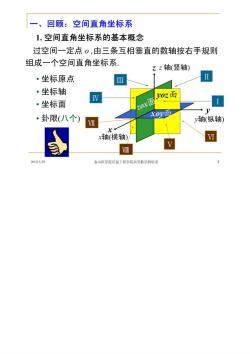
一、回顾：空间直角坐标系 1.空间直角坐标系的基本概念 过空间一定点0，由三条互相垂直的数轴按右手规则 组成一个空间直角坐标系， zz轴（竖轴） ·坐标原点 ·坐标轴 y0z面 ·坐标面 ·卦限（八个） x0y面 y轴（纵轴） 1 x轴（横轴） I 2012329 秦山医学院信息工程学院高等数学教研室

在直角坐标系下 点M←11→有序数组（化，y,z)(称为点M的坐标） 特殊点的坐标： 原点00,0,0)； 坐标面上的点A,B,C R(0,0,z) B(0,y,z) C(x,0,z) 坐标轴上的点P,Q,R; Q(0,y,0) xP(x,0,0) A(x,y,0) 2012329 奉山医学院信息工程学院高等数学教研宝

两点间的距离公式： B A(1,Z)B(x2,y2,22), AB=Vx2-)2+0y-)2+(22-2)2 M(x,y,z) 0(0,0,0) 10M=x2+y2+z2 2012329 泰山医学院信息工程学院高等数学教研室

例1.求证以M1(4,3,1),M2(7,1,2),M3(5,2,3)为顶点 的三角形是等腰三角形. 证： M,M22=(7-42+1-3)2+(2-1)2=14 M,M,=(5-7)2+(2-1)2+(3-2)2=6 1M,M2=(5-4)2+(2-3)2+(3-102=6 ∴.M2M3=M1M3 M M 即△M1M2M3为等腰三角形 M2 2012329 泰山医学院信息工程学院高等数学教研室

例2.在轴上求与两点A(-4,1,7)及B(3,5,-2)等距 离的点 解：设该点为M(0,0,z),因为MA=MB, V(-4)2+12+(7-z)2=V32+52+(-2-z)7 解得z=号，故所求点为M(0,0,). 思考题： (1)在坐标面上和坐标轴上的点的坐标各有什么特征？ (2)指出下列各点的位置： A(3,4,0):B(0,4,3):C(3,0,0):D0,-1,0) 2012329 泰山医学院信息工程学院高等数学教研室

二、向量(Vector)的概念 向量：既有大小又有方向的量 向量表示：向量用一条有方向的线段 (称为有向线段)表示 (1)有向线段的长度表示方向的大小 有向线段的方向表示向量的方向 (2)以A为起点、B为终点的有向线段 所表示的向量记作AB (3)向量可用粗体字母、或加箭头的书写体字母表示 w例如，a、F感。京

自由向量：与起点无关的向量，称为自由向量。 向量的模：向量的大小（长度）或|M,M, 单位向量：模长为1的向量.a或M,M, 零向量：0模长为0的向量（它的方向是任意的）· 负向量：大小相等但方向相反的向量 a=-b 向量相等：如果向量a和b的大小相等，且方向相同，则 称向量a和b是相等的，记为a=b. a 相等的向量经过平移后可以完全重合， b 2012329 泰山医学院信息工程学院高等数学教研室

向量的平行：两个非零向量如果它们的方向相同或相反，就 称这两个向量平行 a 向量a与b平行，记作al/b. b 零向量认为是与任何向量都平行. al/bllc 共线向量：当两个平行向量的起点放在同一点时，它们的 终点和公共的起点在一条直线上.因此，两向量平行 又称两向量共线。 共面向量：设有(23)个向量，当把它们的起点放在同一点 时，如果k个终点和公共起点在一个平面上，就称这k个向量 共面. 2012.329 泰山医学院信息工程学院高等数学教研室 9

三、向量的线性运算(Operations of Vectors) 1.向量的加法 设有两个向量a与b,平移向量，使b的起点与a的终点重 合，则从a的起点到b的终点的向量c称为向量a与b的和，记 作a+b,即c=a+b. 平行四边形法则 或三角形法则： a 2012329 泰山医学院信息工程学院高等数学教研留