山东第一医科大学（泰山医学院）：《高等数学》课程教学课件（打印版）第三章 微分中值定理与导数的应用

第三章微分中值定理与导数的应用 第一节微分中值定理 第二节 洛必达法则 第三节 泰勒公式 第四节 函数的单调性与曲线的凹凸性 第五节 函数的极值与最大值最小值 第六节 函数图形的描绘 第七节 曲率 2012-3-29 泰山医学院信息工程学院高等数学教研室 1

第一节微分中值定理 (The Mean Value Theorem) 问题的提出 二 微分中值定理 1费马(Fermat)引理 2罗尔(Rolle)定理 3拉格朗日(Lagrange)中值定理 4柯西(Cauchy)中值定理 三小结与思考判断题 2012329 素山医学院信息工程学院高等数学教研室

一 问题的提出(Introduction) 我们知道，导数是刻划函数在一点处变化率 的数学模型，它反映的是函数在一点处的局部变 化性态，但在理论研究和实际应用中，常常需要 把握函数在某区间上的整体变化性态，那么函数 的整体变化性态与局部变化性态有何关系呢？中 值定理正是对这一问题的理论诠释。 中值定理揭示了函数在某区间上的整体性质与该 区间内部某一点的导数之间的关系。中值定理既 是利用微分学知识解决应用问题的数学模型，又 是解决微分学自身发展的一种理论性数学模型。 2012329 泰山医学院信息工程学院高等数学教研室 3

二微分中值定理The Mean Value Theorem) 微分中值定理的核心是拉格朗日(Lagrange) 中值定理，费马引理是它的预备定理，罗尔定理 是它的特例，柯西定理是它的推广。 1预备定理一费马(Fermat)定理 设函数f(x)在点x的某邻域U(x)内有定义， 且在x,可导，若对x∈U(x),有f(x)≤f(x) (或f(x)≥f(x),则f'(x)=0. 费马(Fermat,1601-1665),法国人，与笛卡尔 共同创立解析几何。因提出费马大、小定理而著于世。 2012329 泰山医学院信息工程学院高等数学教研室

证明：不妨设x∈U(x)时，f(x)≤f(x),于是对于 x,+△xeU(x),有f(x+A)≤f(x) 当Ax>0时，f+A)-f,2≤0店 △x 当△x<0时f,+a)-fx,≥； △x 根据函数∫田在x,可导的条件，极限的保号性，便得到 )=)=lim +Ax)-0 △r-→0 )()lim(+Ax)-f( △r→0 所以'(x)=0 2012329 素山医学院信息工程学院高等数学教研室

几何解释： v=f(x) 曲线在最高点和最低点 显然有水平切线，其斜 率为0，当切线沿曲线连 bξ2b 续滑动时，就必然经过 位于水平位置的那一点， 2012329 泰山医学院信息工程学院高等数学教研室

2 罗尔Rolle)定理(Rolle's Theorem) 罗尔(RolIe)定理如果函数f(x)在闭区间[a,b) 上连续，在开区间(，b)内可导，且在区间端点的函数 值相等，即f(a)=f(b),那末在(a,b)内至少有一点 (a<5<b),使得函数f(x)在该点的导数等于零， 即f(传)=0 y=f(x) B 几何解释： o a ξ2bx 连续曲线弧AB上至少有一点C,在该点处的切线是水平的. 2012329 泰山医学院信息工程学院高等数学教研家

证：f(x)在[a,b]连续，必有最大值M和最小值m. ()若M=m.则f(x)=M. 由此得f'(x)=0.5∈(a,b),都有f'(传)=0. (2)若M≠m.:f(a)=f(b), .最值不可能同时在端点取得. 设M≠f(a), 则在(a,b)内至少存在一点5使f(5)=M. 因此，x∈[a,bl,有f(x)≤f(5), 从而由费马引理得'(5)=0， 2012329 泰山医学院信息工程学院高等数学教研室

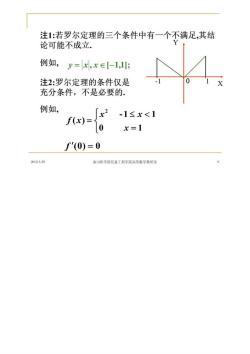
注1：若罗尔定理的三个条件中有一个不满足，其结 论可能不成立， 例如，y=x,x∈-1,1 注2：罗尔定理的条件仅是 充分条件，不是必要的. 例如， [x2 -1≤x<1 f(x)= 0 x=1 '(0)=0 2012329 素山医学院行息工程学院高等数学教研室

例1证明方程x5+x-1=0有且仅有一个正实根. 证：1)存在性 设f(x)=x5+x-1,则f(x)在0,1连续， 且f(0)=-1,f)=1.由零点定理 3x。∈(0,1)，使f(x)=0.即为方程的正实根. 2)唯一性 设另有x1∈(0,1)，x1≠x,使f(x)=0. “f()在x,x,之间满足罗尔定理的条件， 至少存在一个5（在xx1之间），使得f'()=0. 但f'(x)=5x4+1>0(x∈(0,1)矛盾，.为唯一实根 2012329 泰山医学院信息工程学院高等数学教研室 10