中国科学技术大学：《光学 Optics》课程教学课件（PPT讲稿）Chapter 1 几何光学 Geometrical Optics 1.4 薄透镜成像

1.4薄透镜成像

1.4 薄透镜成像

、 薄透镜 透镜 透镜：由两个折射球面构成的 光具组，球面间为透镜媒质。 2 薄透镜 02 由两个折射球面组成，过两 球面圆心的直线为光轴，顶 点间距d。如果满足： 通常情况下n=n'≈1 d<<r,n,s,s' 就是薄透镜，通常可以认为d=O 此时，两球面顶点重合，称为光心，记为O

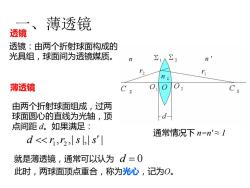
一、薄透镜 透镜：由两个折射球面构成的 光具组，球面间为透镜媒质。 薄透镜 透镜 由两个折射球面组成，过两 球面圆心的直线为光轴，顶 点间距 d。如果满足： , ,| |,| | 1 2 d  r r s s  就是薄透镜，通常可以认为 d = 0 此时，两球面顶点重合，称为光心，记为O。 通常情况下 n=n' ≈ 1

逐次成像法 ① 成像透镜由两个折射球面组成，透镜使光线经过了两个球 面的折射。 ②可以用逐次成像法得到透镜的成像公式。 ③ 物Q经第一面折射成像Q'1（应用物像关系可确定像)。 ④ Q'1无论虚实，对第二面来说都等效于物。 ⑤ Q'1作为第二面的物，经第二面折射成像Q'2（再次应用 物像关系可确定像)。 反复应用上述方法，可得到最终的像

逐次成像法 ① 成像透镜由两个折射球面组成，透镜使光线经过了两个球 面的折射。 ② 可以用逐次成像法得到透镜的成像公式。 ③ 物𝑄经第一面折射成像Q′ 1 （应用物像关系可确定像）。 ④ Q′ 1 无论虚实，对第二面来说都等效于物。 ⑤ Q′ 1 作为第二面的物，经第二面折射成像Q′ 2 （再次应用 物像关系可确定像）。 ⑥ 反复应用上述方法，可得到最终的像

厚透镜的逐次成像 n 虚物Q'经过Σ再一次成像 C S2 S 第一次成像 ntn-n-n si St 第二次成像： hn4_川- _n' +n='-nz S2 S2 s2 d-s 整体成像：S1=S,S2=S n' n 十一 n-n+1'-n s's d-s

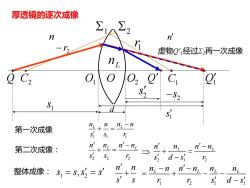
厚透镜的逐次成像 L n 1 2 Q1 Q Q  n n  1 r 2 − r 1s 1s 2 s d C2 O1 O O2 C1 虚物Q'1经过Σ2再一次成像 2 −s 第一次成像 1 1 1 L L n n n n s s r− + =  第二次成像： 2 2 2 L L n n n n s s r   − + =  2 1 2 L L n n n n s d s r   − + =   −  整体成像： 1 2 1 1 L L L L n n n n n n r r s d s − − = + − −   − n n s s  +  1 2 s s s s = = ,  

薄透镜成像的物像关系 薄透镜的特性，d≈O n'n n-n.n'-n n S '2 s d-s ±”=h-n+n-ny n[-n → n-nL=Φ2 ”+”=中，+，=ΦΦ=n,-n+n- s's r 12 只有在薄透镜，及d0的条件下，才有Φ，+Φ2=Φ 薄透镜的光焦度，单位是屈光度(diopter,D),对于眼镜，度数为lO0Φ

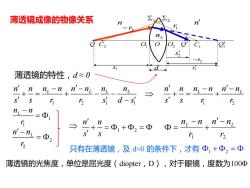
薄透镜成像的物像关系 nL 1 2 Q1 Q Q  n n  1 r 2 − r 1s 1s 2 s d C2 O1 O O2 C12 −s 1 2 1 1 L L L L n n n n n n n n s s r r s d s   − − + = + − −    − 薄透镜的特性，d ≈ 0 1 2 L L n n n n n n s s r r   − − + = +   1 2 n n s s  + =  +  =   1 1 L n n r− =  2 2 L n n r  − =   1 2 r n n r nL n − L  + −  = 薄透镜的光焦度，单位是屈光度（diopter，D），对于眼镜，度数为100Φ 只有在薄透镜，及 d≈0 的条件下，才有  +  =  1 2

薄透镜的焦距公式 n =00f= n-nin-n 物方焦距 n',n n-n,n'-n s'S S=00f'= n' n 像方焦距 n-n:n-n Φ

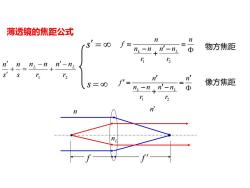
1 2 r n n r n n s n s n L − L  + − + =   s  =  1 2 L L n n f n n n n r r  = = − − + 物方焦距 1 2 L L n n f n n n n r r     = = − − + s =  像方焦距 L n n n  f f  薄透镜的焦距公式

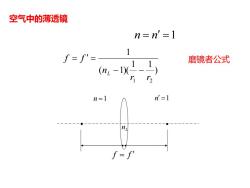
空气中的薄透镜 n=n'=1 1 f=f'= 磨镜者公式 n=l n'=1 n

n = n  =1 ) 1 1 ( 1)( 1 1 2 r r n f f L − − =  = 磨镜者公式 nL n =1 n  =1 f f =  空气中的薄透镜

Gauss物像公式-距离从光心算起 2 S=S d→0s'=S2S2≈-51 +)=1 s's n n-n n'-ns' n n-nin-n n n' f n n-n n'-n

Gauss物像公式 - 距离从光心算起 Q Q1 1 s 1 s  d 1 2 2 s 2 s  Q n nL n  d → 0 1 2 r n n r n n s n s n L − L  + − + =   ( ) 1 1 1 2 + =    − + − s n s n r n n r n n L L 1 s s = 2 s s   = 2 1 s s  −  1 f f s s  + =  1 2 L L n f n n n n r r = − − +  1 2 L L n f n n n n r r   = − − +  f n f n =  

成像的基本光学单元 ·凡是存在简单的物像关系，而且其中的距离有共同的度量 起点，即可以用下述公式描述的光学器件 n' 是成像光具组的基本单元 ·单个折射面、反射面，以及薄透镜，都是基本的成像单元 厚透镜不是基本的成像单元，是两个折射球面构成的光具 组，用逐次成像法求解

成像的基本光学单元 • 凡是存在简单的物像关系，而且其中的距离有共同的度量 起点，即可以用下述公式描述的光学器件 是成像光具组的基本单元 n n s s  + =   1 f f s s  + =  • 单个折射面、反射面，以及薄透镜，都是基本的成像单元 • 厚透镜不是基本的成像单元，是两个折射球面构成的光具 组，用逐次成像法求解

二、 薄透镜的光学参数与光学特性 正透镜和负透镜 ①焦距为正值(f和f'>0)的透镜是正透镜；焦距为负值 (f和f'<0)的透镜是负透镜。 ② 正透镜的像方焦点在光线出射方（具有实焦点）；负透 镜的像方焦点在光线入射方（具有虚焦点）。 ③ 正透镜使入射的平行光汇聚在像方焦点；负透镜使入射 的平行光发散，反向延长线通过像方焦点。 ④空气中，中间厚边缘薄的透镜是正透镜；中间薄边缘厚 的透镜是负透镜

① 焦距为正值（f 和 f’ >0）的透镜是正透镜；焦距为负值 （f 和 f’ <0）的透镜是负透镜。 ② 正透镜的像方焦点在光线出射方（具有实焦点）；负透 镜的像方焦点在光线入射方（具有虚焦点）。 ③ 正透镜使入射的平行光汇聚在像方焦点；负透镜使入射 的平行光发散，反向延长线通过像方焦点。 ④ 空气中，中间厚边缘薄的透镜是正透镜；中间薄边缘厚 的透镜是负透镜。 正透镜和负透镜 二、薄透镜的光学参数与光学特性