中国科学技术大学：《光学 Optics》课程教学课件（PPT讲稿）Chapter 4 光的衍射 Diffraction of Light 4.5 衍射光栅

4.5衍射光栅 多缝夫琅禾费衍射 光栅光谱仪

4.5 衍射光栅 多缝夫琅禾费衍射 光栅光谱仪

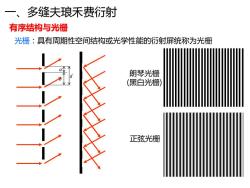
一、 多缝夫琅禾费衍射 有序结构与光栅 光栅：具有周期性空间结构或光学性能的衍射屏统称为光栅 朗琴光栅 (黑白光栅) 正弦光栅

一、多缝夫琅禾费衍射 有序结构与光栅 光栅：具有周期性空间结构或光学性能的衍射屏统称为光栅 a b d 朗琴光栅 (黑白光栅) 正弦光栅

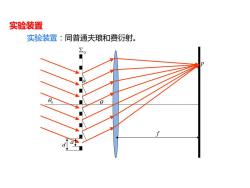
实验装置 实验装置：同普通夫琅和费衍射

实验装置 实验装置：同普通夫琅和费衍射。   a d P 0 f 0

分析思路 ①经过光栅的所有光波，进行相干叠加。 ②光栅的每一个单元，是次波的叠加，按衍射分析； ③不同的单元之间，是分立的衍射波之间的叠加，按干涉分析

分析思路 ① 经过光栅的所有光波，进行相干叠加。 ② 光栅的每一个单元，是次波的叠加，按衍射分析； ③ 不同的单元之间，是分立的衍射波之间的叠加，按干涉分析。 d a d a

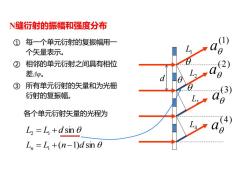
N缝衍射的振幅和强度分布 ①每一个单元衍射的复振幅用一 个矢量表示。 ② 相邻的单元衍射之间具有相位 差4p。 ③ 所有单元衍射的矢量和为光栅 衍射的复振幅。 各个单元衍射矢量的光程为 L=L+dsin 0 L=L+(n-1)dsin 0

N缝衍射的振幅和强度分布 ① 每一个单元衍射的复振幅用一 个矢量表示。 ② 相邻的单元衍射之间具有相位 差Δφ。 ③ 所有单元衍射的矢量和为光栅 衍射的复振幅。  d  L1 L2 L3 L4 (1) a (2) a (3) a (4) a  L2 = L1 + d sin  Ln = L1 + (n −1)d sin  各个单元衍射矢量的光程为

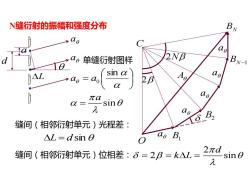
N缝衍射的振幅和强度分布 BN ae 00 ae单缝衍射图样 2NB BN △ sin a ae πa ae X= sin a 缝间（相邻衍射单元）光程差： 1®B △L=dsin 0 ao B 缝间（相邻衍射单元）位相差：δ=2B=kAL= 2πd sine

N缝衍射的振幅和强度分布 缝间（相邻衍射单元）光程差： 缝间（相邻衍射单元）位相差： L = d sin 2 2 sin d k L      = =  =  L d a a a a a a a C O  B1 B2 BN−1 BN 2 A 2N       =    sin a a0 sin a    = a 单缝衍射图样

BN N缝行射的振幅和强度分布 a NB BN OB=Ap=20Csin NB ag 2sin6→4。=ag sin NB ae OC= sin B 16B ao B 1=46=a sin sin NB a 其中： sin B a=. Ta sin 0 单缝衍射因子 缝间干涉因子 B= πd (单元因子) (N元干涉因子) -sin 0 说明：在光栅的缝宽和缝间距一定的情况下，干涉的光强结果和 波长以及角度有关，这也就决定了相同波长的单色光在不同角度 下，干涉所得的光强不同；不同波长的光在相同角度下，干涉所 得的光强也不同

N缝衍射的振幅和强度分布     sin sin N A = a 其中：     sin a =     sin d = 单缝衍射因子 （单元因子） 缝间干涉因子 （N元干涉因子） 2 2 2 2 0 sin sin sin N I A a           = =         OB A OC N N = =  2 sin  a a a a a C O  B1 B2 BN−1 BN 2 A 2N 说明：在光栅的缝宽和缝间距一定的情况下，干涉的光强结果和 波长以及角度有关，这也就决定了相同波长的单色光在不同角度 下，干涉所得的光强不同；不同波长的光在相同角度下，干涉所 得的光强也不同。 2sin a OC   = 

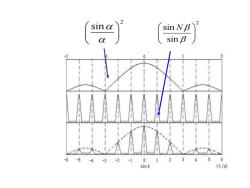
sin NB sin 0 6 (a/d)

2 sin        2 sin sin N       

缝间干涉因子的特点 sin NB B= sin 0 (1)主极大： sin B ①位置 B-Jr→sim0=j话 j=0,±1,2，.，±n ②数目 jmax=[d/a] (sin0<1) ③强度 SinNB=N sin B 1Um)=1,(3naN2 单缝的NP倍 说明：主极大的强度与N有关，位置与N无关

缝间干涉因子的特点 ① 位置 sin j d   = j n =    0, 1, 2, , ② 数目 j d max =   ③ 强度 单缝的 N2 倍 （1）主极大： (sin  1) 说明：主极大的强度与N 有关，位置与N 无关 sin sin N N   =   = j  2 2 0 sin I j I N ( ) ( )    = 2 sin sin N            sin d =

缝间干涉因子的特点 (2)零点和次级大： 干涉因子极小值 sinNB=0→NB=mnB≠nm sin B sin0=m2/Nd,sin0≠nλ/d sin=[0],A/Nd,.(N-1)A/Nd,[a/d], (N+1)z/Wd,(W+2)z/Nd,.(2N-1)2/Nd,[2/dl,. 零点： 位益sm9=(+)月 j=0,±1，±2，.，±n m=1,2,.2w21 个数：N1(两个主极大之间) 次极大：每两个相邻暗线之间存在一个次级大，共N-2个 (两个主极大之间)

缝间干涉因子的特点 （2）零点和次级大： 位置 sin m j N d     = +     0, 1, 2, , 1,2, , 1 j n m N  =      = − 零点： 次极大：每两个相邻暗线之间存在一个次级大，共N-2个 （两个主极大之间）。       sin 0 , / , ( 1) / , / , ( 1) / ,( 2) / , (2 1) / , 2 / , Nd N Nd d N Nd N Nd N Nd d         = − + + − 干涉因子极小值 sin / , sin /     =  m Nd n d sin 0 sin N  =  N m   =    n 个数：N-1（两个主极大之间）