上海交通大学：《概率论与数理统计》课程教学资源（课件讲义）第四章 随机变量的数字特征 4.1 数学期望

第四章 随机变量的数字特征

第四章 随机变量的数字特征

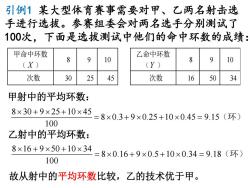
引例1某大型体育赛事需要对甲、乙两名射击选 手进行选拔。参赛组委会对两名选手分别测试了 100次，下面是选拔测试中他们的命中环数的成绩： 甲命中环数 乙命中环数 8 10 8 9 10 (X) (Y) 次数 30 25 45 次数 16 50 34 甲射中的平均环数： 8×30+9×25+10×45 = 8×0.3+9×0.25+10×0.45=9.15（环) 100 乙射中的平均环数： 8×16+9×50+10×34 =8×0.16+9×0.5+10×0.34=9.18(环) 100 故从射中的平均环数比较，乙的技术优于甲

引例1 某大型体育赛事需要对甲、乙两名射击选 手进行选拔。参赛组委会对两名选手分别测试了 100次，下面是选拔测试中他们的命中环数的成绩： 甲命中环数 （ X ） 8 9 10 次数 30 25 45 乙命中环数 （Y ） 8 9 10 次数 16 50 34 甲射中的平均环数： 8 30 9 25 10 45 8 0.3 9 0.25 10 0.45 9.15 100 × +× + × =× +× + × = （环） 乙射中的平均环数： 8 16 9 50 10 34 8 0.16 9 0.5 10 0.34 9.18 100 × +× + × =× +× + × = （环） 故从射中的平均环数比较，乙的技术优于甲

引例2假设两个风险资产的收益X,Y都服从正 态分布（而事务界也常常用正态分布估计风险资 产的收益)，假设两个资产收益率分布具体为： X≈N(8,4) Y~N(8,9) (单位：百分比)。投资者对这两个资产该做什 么决策？其依据是什么？ 0.2 N(8,9) 0.15 N(8.4) 0.1 0.05 0 8 10 15 20

引例2 假设两个风险资产的收益 X，Y 都服从正 态分布（而事务界也常常用正态分布估计风险资 产的收益），假设两个资产收益率分布具体为： X N ~ (8, 4) Y N ~ (8,9) （单位：百分比）。投资者对这两个资产该做什 么决策？其依据是什么？

随机变量的平均取值一数学 本章内容 期望 随机变量取值平均偏离平均值的 情况一 方差 描述两个随机变量之间的某种关 系的数一 协方差与相关系数

 随机变量的平均取值 —— 数学 期望  随机变量取值平均偏离平均值的 情况 —— 方差  描述两个随机变量之间的某种关 系的数 —— 协方差与相关系数 本 章 内 容

4.1数学期望 定义1离散型随机变量的数学期望 设离散型随机变量X的分布律为 P(X=x)=p,k=1,2,… 若无穷级数 XkPk k=1 绝对收敛，则称其和为随机变量X的数学期望 记为 EX=∑xP k=1

设离散型随机变量X 的分布律为 ( ) , 1,2, PX x p k k k = = =  若无穷级数 1 k k k x p +∞ = ∑ 绝对收敛，则称其和为随机变量 X 的数学期望 记为 1 k k k EX x p +∞ = = ∑ 定义1 离散型随机变量的数学期望 4.1 数学期望

定义2连续型随机变量的数学期望 设连续型随机变量X的概率密度为f(x) 若积分 f(x)d 绝对收敛，则称此积分的值为随机变量X的 数学期望，记为 EX=∫f(x)d 数学期望简称期望，又称均值 注意：数学期望反映了随机变量取值的平均值， 它是一种加权平均

设连续型随机变量X 的概率密度为 f (x) 若积分 ∫ +∞ −∞ xf (x)dx 绝对收敛，则称此积分的值为随机变量 X 的 数学期望，记为 EX xf x dx ( ) +∞ −∞ = ∫ 数学期望简称期望，又称均值 注意:数学期望反映了随机变量取值的平均值, 它是一种加权平均 定义2 连续型随机变量的数学期望

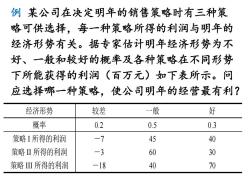
例某公司在决定明年的销售策略时有三种策 略可供选择，每一种策略所得的利润与明年的 经济形势有关。据专家估计明年经济形势为不 好、一般和较好的概率及各种策略在不同形势 下所能获得的利润（百万元)如下表所示。问 应选择哪一种策略，使公司明年的经营最有利？ 经济形势 较差 一般 好 概率 0.2 0.5 0.3 策略I所得的利润 -7 45 40 策略Ⅱ所得的利润 -3 60 30 策略Ⅲ所得的利润 -18 40 70

例 某公司在决定明年的销售策略时有三种策 略可供选择，每一种策略所得的利润与明年的 经济形势有关。据专家估计明年经济形势为不 好、一般和较好的概率及各种策略在不同形势 下所能获得的利润（百万元）如下表所示。问 应选择哪一种策略，使公司明年的经营最有利？ 经济形势 较差 一般 好 概率 0.2 0.5 0.3 策略 I 所得的利润 －7 45 40 策略 II 所得的利润 －3 60 30 策略 III 所得的利润 －18 40 70

解设随机变量X表示第i种策略(i=1,2,3),则 三种策略所能获得的平均利润为 E(X)=-7×0.2+45×0.5+40×0.3=33.1(元) E(X2)=-3×0.2+60×0.5+30×0.3=38.4(元) E(X3）=-18×0.2+40×0.5+70×0.3=37.4(元) 所以如仅仅根据平均利润来选择策略的话，应选择 第2种策略

解 设随机变量 Xi 表示第 i 种策略（i = 1，2，3），则 三种策略所能获得的平均利润为 1 E X( ) 7 0.2 45 0.5 40 0.3 33.1 ( ) =− × + × + × = 元 2 E X( ) 3 0.2 60 0.5 30 0.3 38.4 ( ) =− × + × + × = 元 ( ) 3 E X =− × + × + × = 18 0.2 40 0.5 70 0.3 37.4 ( ) 元 所以如仅仅根据平均利润来选择策略的话，应选择 第2种策略

例据统计每周末光顾上海某教育超市的人数 服从参数为入的泊松分布，求本周末光顾该 教育超市的平均人数。 解：设本周末光顾该教育超市的人数为X,由题设知 P(X=k)= e2, k=0,1,2,… k e2= 0 k三 台(k-1)9 故本周末光顾该教育超市的平均人数为λ

例 据统计每周末光顾上海某教育超市的人数 服从参数为 λ 的泊松分布，求本周末光顾该 教育超市的平均人数。 解：设本周末光顾该教育超市的人数为 X，由题设知 ( ) , 0,1,2, ! k PX k e k k λ −λ = = =  ( ) 1 1 1 ! ( 1)! k k k k EX k e e k k λ λ λ λ λ λ ∞ ∞ − − − = = = = = − ∑ ∑ 故本周末光顾该教育超市的平均人数为 λ

例假设挂在某购物网站一个广告的点击率为卫， 网站的每个访客是否点击该广告相互独立，X表 示首次点击这个广告时该网站的访客量。求首次 点击该广告的时候，这个网站的平均访客量。 解：由题设，易知X服从参数为为卫的几何分布，即 P(X=k)=pg-,k=1,2,… ('-n品r小-{0

例 假设挂在某购物网站一个广告的点击率为 p， 网站的每个访客是否点击该广告相互独立，X 表 示首次点击这个广告时该网站的访客量。求首次 点击该广告的时候，这个网站的平均访客量。 解：由题设，易知 X 服从参数为为 p 的几何分布，即 1 ( ) , 1,2, k P X k pq k − = = =  ( ) 1 1 1 1 1 k k k k d dq E X kpq p q p dq dq q p ∞ ∞ − = =     = = = =         − ∑ ∑