《经济数学》课程教学课件（PPT讲稿）第五章 定积分 5-2 微积分基本公式

微积分基本公式 在上一节我们已经看到，直接用定义 计算定积分是十分繁难的，因此我们期 望寻求一种计算定积分的简便而又一般 的方法。我们将会发现定积分与不定积 分之间有着十分密切的联系，从而可以 利用不定积分来计算定积分

在上一节我们已经看到，直接用定义 计算定积分是十分繁难的，因此我们期 望寻求一种计算定积分的简便而又一般 的方法。我们将会发现定积分与不定积 分之间有着十分密切的联系，从而可以 利用不定积分来计算定积分。 微积分基本公式

一、问题的提出 变速直线运动中位置函数与速度函数的联系 设某物体作直线运动，已知速度y=v(t)是时 间间隔T,T,]t的一个连续函数，且v(t)≥0， 求物体在这段时间内所经过的路程， 变速直线运动中路程为)山 另一方面这段路程可表示为S(T,)-(T) 0)dt=sT)-s(T).其中s0)=

变速直线运动中位置函数与速度函数的联系 设某物体作直线运动，已知速度v = v(t)是时 间间隔[ , ] T1 T2 上t 的一个连续函数，且v(t)  0， 求物体在这段时间内所经过的路程. 变速直线运动中路程为  2 1 ( ) T T v t dt 另一方面这段路程可表示为 ( ) ( ) 2 T1 s T − s ( ) ( ) ( ). 2 1 2 1 v t dt s T s T T T  = −  其中 s(t) = v(t). 一、问题的提出

二、积分上限函数及其导数 设函数f(x)在区间[M,b]上连续，并且设x 为a,b]上的一点，考察定积分 ∫fx)k=f) 如果上限x在区间4，b1上任意变动，则对于 每一个取定的x值，定积分有一个对应值，所以 它在[，b]上定义了一个函数， 记(x)=f()t.积分上限函数

设函数 f (x)在区间[a,b]上连续，并且设x 为[a,b]上的一点，  x a f (x)dx 考察定积分  = x a f (t)dt 如果上限x在区间[a,b]上任意变动，则对于 每一个取定的x值，定积分有一个对应值，所以 它在[a,b]上定义了一个函数， ( ) ( ) .   = x a 记 x f t dt 积分上限函数 二、积分上限函数及其导数

积分上限函数的性质 定理1如果f(x)在@，b]上连续，则积分上限的函 数Φ(x)=f(t)t在a,b]上具有导数，且它的导 数是0o)=杰fh=) (a≤x≤b) 证Φ(x+△x)=∫+arft) △Φ=Φ(x+△x)-Φ(x) Φ(x) -"f(oyh-T f(oydr xx+△xbx

a b x y o 定理１ 如果 f ( x)在[a,b]上连续，则积分上限的函 数 x f t dt x a ( ) = ( ) 在[a,b]上具有导数，且它的导 数是 ( ) f (t)dt f (x) dx d x x a  =  = (a  x  b) 积分上限函数的性质 x + x 证 x x f t dt x x a + ( +  ) = ( )  = (x + x) − (x) f t dt f t dt x a x x a  = − + ( ) ( ) (x) x

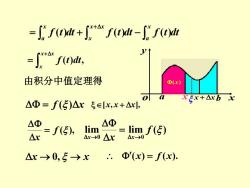
=∫ft+∫+f)t-f)t =∫f0, 由积分中值定理得 ①(x) 0 xEx+△xb △Φ=f(5)△x∈x,x+△， 专，m △Φ △x-→0△X =limf(传) △x→0 △x→0,5→x.Φ'(x)=f(x)

 f t dt f t dt f t dt x a x x x x = a +  −  + ( ) ( ) ( ) ( ) ,  + = x x x f t dt 由积分中值定理得  = f ( )x [x, x + x], x → 0, → x f ( ), x =   lim lim ( ) 0 0 f  x→ x x→ =   (x) = f (x). a b x y o x + x (x) x

注 此定理表明连续函数取变上限定积分再对 上限自变量x求导，其结果就等于被积 函数在上限自变量x处的函数值 若上限不是x而是x的函数心)， 则求导时必须按复合函数的求导法则进行 d ax) (d=fa(x) 一般情况如果ft)连续，a(x)、b(x)可导， 则F)=feh的导数Fx)为 F-&fea=fioi-f树

一般情况 如 果 f (t)连续，a(x)、b(x)可导， 则F x f t dt b x a x  = ( ) ( ) ( ) ( ) 的导数F(x)为   = ( ) ( ) ( ) ( ) b x a x f t dt dx d F x = f b(x)b(x) − f a(x)a(x) 注 此定理表明连续函数取变上限定积分再对 上限自变量 x 求导，其结果就等于被积 函数在上限自变量 x 处的函数值 若上限不是 x 而是 x 的函数 a(x)， 则求导时必须按复合函数的求导法则进行  =  ( ) [ ( ) ] [ ( )] ( ) a x a f t dt f a x a x dx d

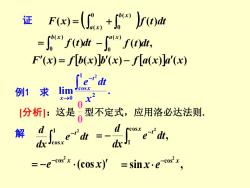
证 F)=(a+e) -fy-fod, F'(x)=fb(x)]b'(x)-fa(x)】]a'(x) ["edt 例1求im cosx x-→0 k2 0 [分析]：这是。型不定式，应用洛必达法则 解 =-eox.(cosx)=sinx.e-cx

F x ( )f t dt a x b x ( ) ( ) 0 ( ) ( )  0 = + f t dt b x =  ( ) 0 ( ) ( ) , ( ) 0 f t dt a x  − F(x) = f b(x)b(x) − f a(x)a(x) 例1 求 lim . 2 1 cos 0 2 x e dt x t x  − → 0 0 [分析]：这是 型不定式，应用洛必达法则. 解  − 1 cos 2 x t e dt dx d , cos 1 2  − = − x t e dt dx d (cos ) 2 cos = −   − e x x sin , 2 cos x x e − =  证

1 lim Sinx·ecos2x x-→0 -→0 2x 2e 例2设f(x)在(-oo,+oo)内连续，且f(x)>0. 证明函数F(x)= (t) 一在(0，+∞)内为单调增 心ft) 加函数. 证 云fo= 杰f0t=fx

2 1 cos 0 2 lim x e dt x t x  − → x x e x x 2 sin lim 2 cos 0 − →  = . 2 1 e = 例 2 设 f (x)在(−,+)内连续，且 f (x)  0. 证明函数   = x x f t dt tf t dt F x 0 0 ( ) ( ) ( ) 在(0,+)内为单调增 加函数. 证  x tf t dt dx d 0 ( ) = xf (x)  x f t dt dx d 0 ( ) = f (x)

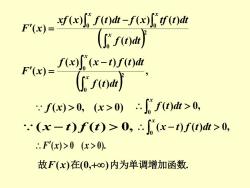
F'=wft-fx)fed （fe)j )Toofn roa 'f(x)>0,(x>0).f(t)dt>0, .(x-t)f(t)>0,.n(x-t)f(t)t>0, .F'(x)>0(x>0). 故F(x)在(0，+∞)内为单调增加函数

( ) , ( ) ( ) ( ) ( ) ( ) 2 0 0   −  = x x f t dt f x x t f t dt F x  f (x)  0, (x  0) ( ) 0, 0   x f t dt ( ) 2 0 0 0 ( ) ( ) ( ) ( ) ( ) ( )    −  = x x x f t dt xf x f t dt f x tf t dt F x (x − t) f (t)  0, ( ) ( ) 0, 0  −  x x t f t dt F(x)  0 (x  0). 故F(x)在(0,+)内为单调增加函数

例3设f(x)0,1上连续，且f(x)0, F(x)在0,1上为单调增加函数 F(0)=-10 所以F(x)=0即原方程在0,1]上只有一个解

例 3 设 f (x)在[0,1]上连续，且f (x)  1.证明 2 ( ) 1 0 x −  f t dt = x 在[0,1]上只有一个解. 证 令 ( ) 2 ( ) 1, 0 = − −  F x x f t dt x  f (x)  1, F(x) = 2 − f (x)  0, F(x)在[0,1]上为单调增加函数. F(0) = −1  0, = −  1 0 F(1) 1 f (t)dt =  − 1 0 [1 f (t)]dt 所以F(x) = 0即原方程在[0,1]上只有一个解.  0