计算机类本科规划教材：《离散数学》课程配套电子教案（PPT课件讲稿）第9章 图论

第9章图论 第9章图论 91图的基本概念 9.2路和回路 9.3连通图 9.4图的矩阵表示 9.5欧拉图和汉密尔顿图 9.6树 9.7二部图及匹配 9.8平面图 返回总目录

第9章 图论 第9章 图 论 9.1 图的基本概念 9.2 路和回路 9.3 连通图 9.4 图的矩阵表示 9.5 欧拉图和汉密尔顿图 9.6 树 9.7 二部图及匹配 9.8 平面图 返回总目录

第9章图论 第9章图论 图论是一个重要的数学分支。数学家欧拉1736年发 表了关于图论的第一篇论文，解决了著名的哥尼斯堡七 桥问题。克希霍夫对电路网络的研究、凯来在有机化学 的计算中应用了树和生成树的概念。随着科学技术的 发展，图论在运筹学、网络理论、信息论、控制论和计 算机科学等领域都得到广泛的应用。本章首先给出图、 简单图、完全图、子图、路和图的同构等概念，接着研 究了连通图性质和规律，给出了邻接矩阵、可达性矩阵、 连通矩阵和完全关联矩阵的定义。最后介绍了欧拉图与 哈密尔顿图、树、二部图、平面图和图的着色。 返回章目录

第9章 图论 第9章 图论 图论是一个重要的数学分支。数学家欧拉1736年发 表了关于图论的第一篇论文，解决了著名的哥尼斯堡七 桥问题。克希霍夫对电路网络的研究、凯来在有机化学 的计算中都应用了树和生成树的概念。随着科学技术的 发展，图论在运筹学、网络理论、信息论、控制论和计 算机科学等领域都得到广泛的应用。本章首先给出图、 简单图、完全图、子图、路和图的同构等概念，接着研 究了连通图性质和规律，给出了邻接矩阵、可达性矩阵、 连通矩阵和完全关联矩阵的定义。最后介绍了欧拉图与 哈密尔顿图、树、二部图、平面图和图的着色。 返回章目录

第9章图论 9.1图的基本概念 9.1.1图 两个个体x,y的无序序列称为无序对，记为(x,y)。 在无序对(x,y)中，x,y是无序的，它们的顺序可以颠倒， 即(x,y)=(0y,x)。 定义9.1.1图G是一个三重组<G),E(G),0c 其中：(G)是非空结点集。 E(G)是边集。 是边集到结点的有序对或 无序对集合的函数

第9章 图论 9.1图的基本概念 9.1.1图 两个个体x，y的无序序列称为无序对，记为(x,y)。 在无序对(x,y)中，x，y是无序的，它们的顺序可以颠倒， 即(x,y)=(y,x)。 定义9.1.1 图G是一个三重组V(G),E(G),G  其中：V(G)是非空结点集。 E(G)是边集。 G是边集到结点的有序对或 无序对集合的函数

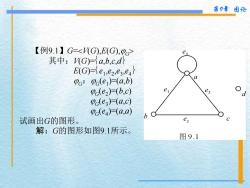
第9章图论 【例9.1】G=<V(G),E(G),pc e 其中：(G)=a,b,c,d E(G)erez.esei PG:Pc(e)(a,b) Pc(e2)-(b,c) e e3 Pc(e:)(a,c) Pc(e)(a,a) b 试画出G的图形。 ez 解：G的图形如图9.1所示。 图9.1

第 9 章 图论 【 例 9 . 1 】 G =  V( G), E ( G), G  其中： V( G)=  a , b , c , d  E ( G)=  e 1 , e 2 , e 3 , e 4  G ： G ( e 1 )=( a , b ) G ( e 2 )=( b , c ) G ( e 3 )=( a , c ) G ( e 4 )=( a , a ) 试画出 G的图形 。 解： G的图形如图 9 . 1所示

第9章图论 由于在不引起混乱的情况下，图的边可以用有序对或 无序对直接表示。因此，图可以简单的表示为： G= 其中：V是非空的结点集。 E是边的有序对或无序对组成的集合。 按照这种表示法，例9.1中的图可以简记为： G- 其中：a,b,c,d} E=(a,b),(b,c),(a,c),(a,a)}

第9章 图论 由于在不引起混乱的情况下，图的边可以用有序对或 无序对直接表示。因此，图可以简单的表示为： G=V,E 其中：V是非空的结点集。 E是边的有序对或无序对组成的集合。 按照这种表示法，例9.1中的图可以简记为： G=V,E 其中：V=a,b,c,d E=(a,b), (b,c), (a,c), (a,a)

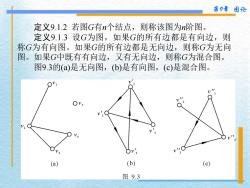
第9章图论 定义9.1.2若图G有n个结点，则称该图为n阶图。 定义9.1.3设G为图，如果G的所有边都是有向边，则 称G为有向图。如果G的所有边都是无向边，则称G为无向 图。如果G中既有有向边，又有无向边，则称G为混合图。 图9.3的(a)是无向图，(b)是有向图，(c是混合图。 OVs V2 (a) (b) (c) 图9.3

第9章 图论 定义9.1.2 若图G有n个结点，则称该图为n阶图。 定义9.1.3 设G为图，如果G的所有边都是有向边，则 称G为有向图。如果G的所有边都是无向边，则称G为无向 图。如果G中既有有向边，又有无向边，则称G为混合图。 图9.3的(a)是无向图，(b)是有向图，(c)是混合图

第9章图论 在一个图中，若两个结点由一条边（有向边或无向边） 关联，则称其中的一个结点是另一个结点的邻接点。并 称这两个结点相互邻接。 在一个图中不与任何结点相邻接的结点，称为孤立 点。 在一个图中，如果两条边关联于同一个结点，则称 其中的一个边是另一个边的邻接边。并称这两个边相互 邻接。关联于同一个结点的一条边叫做环或自回路。在 有向图中环的方向可以是顺时针，也可以是逆时针，它 们是等效的。 定义9.1.4 由孤立点组成的图叫做零图。由一个孤立 点组成的图叫做平凡图。 根据定义9.1.4，平凡图一定是零图

第9章 图论 在一个图中，若两个结点由一条边(有向边或无向边) 关联，则称其中的一个结点是另一个结点的邻接点。并 称这两个结点相互邻接。 在一个图中不与任何结点相邻接的结点，称为孤立 点。 在一个图中，如果两条边关联于同一个结点，则称 其中的一个边是另一个边的邻接边。并称这两个边相互 邻接。关联于同一个结点的一条边叫做环或自回路。在 有向图中环的方向可以是顺时针，也可以是逆时针，它 们是等效的。 定义9.1.4 由孤立点组成的图叫做零图。由一个孤立 点组成的图叫做平凡图。 根据定义9.1.4，平凡图一定是零图

第9章图论 9.1.2结点的度及其性质 定义9.1.5设G=是图，veV,与v相关联的边数 叫做结点v的度。记为deg(v)。规定，自回路为所在结点 增加2度。 在图G=中，度数最大（小）的结点的度叫做图G 的最大（小）度，记为△(G)(⑧(G)。图G的最大度和最小度 表示为： A(G)=maxi deg(v)ve δ(G)=min deg(v)|veVY 在图9.1中，△(G)=4,δ(G)=0

第9章 图论 9.1.2结点的度及其性质 定义9.1.5 设G=V,E是图，vV，与v相关联的边数 叫做结点v的度。记为deg(v)。规定，自回路为所在结点 增加2度。 在图G=V,E中，度数最大(小)的结点的度叫做图G 的最大(小)度，记为(G)((G))。图G的最大度和最小度 表示为： (G)=max deg(v) | vV  (G)= min deg(v) | vV  在图9.1中， (G)=4，(G)=0

第9章图论 定理9.1.1在任何图G=中，所有结点度数的和 等于边数的2倍。即： ∑deg(v)=2El v∈V 证明：图的每一条边都和两个结点相关联，为每个 相关联的结点增加一度，给图增加两度。所以所有结点度 数的和等于边数的2倍。 推论在任何图G=中，度数为奇数的结点必为 偶数个

第9章 图论 定理9.1.1 在任何图G=V,E中，所有结点度数的和 等于边数的2倍。即： = 2|E| 证明：图的每一条边都和两个结点相关联，为每个 相关联的结点增加一度, 给图增加两度。所以所有结点度 数的和等于边数的2倍。 推论 在任何图G=V,E中，度数为奇数的结点必为 偶数个。  vV deg(v)

第9章图论 定义9.1.6设G=是有向图，veV,射入（出）结点 v的边数称为结点v的入（出）度。记为deg(v)(deg+(v)。 显然，任何结点的入度与出度的和等于该结点的度数， deg(v)=deg(v)+deg(v). 定理9.1.2在有向图中，所有结点入度的和等于所有 结点出度的和。 证明：在有向图中每一条边对应一个入度和一个出 度，为图的入度和出度各增加1。所以，所有结点入度的 和等于边数，所有结点出度的和也等于边数

第9章 图论 定义9.1.6 设G=V,E是有向图，vV，射入(出)结点 v的边数称为结点v的入(出)度。记为deg－(v) (deg＋(v))。 显然，任何结点的入度与出度的和等于该结点的度数， 即deg(v)=deg－(v)+deg＋(v)。 定理9.1.2 在有向图中，所有结点入度的和等于所有 结点出度的和。 证明：在有向图中每一条边对应一个入度和一个出 度，为图的入度和出度各增加1。所以，所有结点入度的 和等于边数，所有结点出度的和也等于边数