计算机类本科规划教材：《离散数学》课程配套电子教案（PPT课件讲稿）第4章 二元关系

第4章二元关系 第4章二元关系 4.1二元关系及其表示 4.2关系的运算 4.3关系的性质 4.4关系的闭包运算 4.5等价关系 4.6相容关系 4.7序关系 返回总目录

第4章 二元关系 第4章 二元关系 4.1 二元关系及其表示 4.2 关系的运算 4.3 关系的性质 4.4 关系的闭包运算 4.5 等价关系 4.6 相容关系 4.7 序关系 返回总目录

第4章二元关系 第4章二元关系 4.1二元关系及其表示 4.1.1二元关系的概念 定义4.1.1设A和B是任意集合，如果RcA×B,则称R是 A到B的二元关系。如果R是A到A的二元关系，则称R是A上 的二元关系。 设A=1,2,3},B-a,b},R=。R是A 到B的二元关系。S=了，，，7。S是A上的 二元关系。 定义4.1.2设A和B是任意集合，RCAXB,若∈R, 则称x与y有R关系。记为xRy。若R,则称x与y没有R 关系。记为xRy

第4章 二元关系 第4章 二元关系 4.1二元关系及其表示 4.1.1二元关系的概念 定义4.1.1设A和B是任意集合，如果RA×B，则称R是 A到B的二元关系。如果R是A到A的二元关系，则称R是A上 的二元关系。 设A=1,2,3，B=a,b，R=1,a,2,a,3,b。R是A 到B的二元关系。S=3,1,2,2,2,1,1,1。S是A上的 二元关系。 定义4.1.2设A和B是任意集合，RA×B，若x,yR， 则称x与y有R关系。记为xRy。若x,yR，则称x与y没有R 关系。记为x R y

第4章二元关系 如果R是A到B的二元关系，根据定义4.1.2，∈R与 xRy, R与xRy的意义相同。 定义4.1.3设A和B是任意集合，空集O叫做A到B的空关 系，仍然记为☑。A,B的笛卡尔积AXB叫做A到B的全域关 系，记为E。集合,A到B的全域关系 E=AXB=,,, 定理4.1.1设A是具有n个元素的有限集，则A上的二元关 系有22种。 证明：设A为具有n个元素的有限集，即4=n,由排列组 合原理知AXA=n2? 根据定理3.1.2有P(A×A)F24XL2”2, 即A×A的子集有2”个。所以具有n个元素的有限集A上有2种 二元关系

第4章 二元关系 如果R是A到B的二元关系，根据定义4.1.2，x,yR与 xRy，x,yR与x y的意义相同。 定义4.1.3设A和B是任意集合，空集叫做A到B的空关 系，仍然记为。A，B的笛卡尔积A×B叫做A到B的全域关 系，记为E。集合a,a|aA叫做A上的恒等关系。记为IA。 【例4.1】设A=a,b，B=1,2，求A上的恒等关系IA和 A到B的全域关系A×B。 解：A上的恒等关系IA =a,a,b,b，A到B的全域关系 E =A×B=a,1,a,2,b,1,b,2 定理4.1.1设A是具有n个元素的有限集，则A上的二元关 系有2 n2种。 证明：设A为具有n个元素的有限集，即|A|=n，由排列组 合原理知|A×A|=n 2 。根据定理3.1.2有|P (A×A) |=2 |A×A|=2 ， 即A×A的子集有2 个。所以具有n个元素的有限集A上有2 种 二元关系。 2 n 2 n 2 n R

第4章二元关系 4.1.2二元关系的表示 1.用列举法表示二元关系 例4.1中的A到B的全域关系 E=A×B-,,, A上的恒等关系 I} 都是用列举法表示的。 2.用描述法表示二元关系 设R是实数集，LR|x∈R∧yER∧x≤y,LR是 实数集R上的二元关系

第4章 二元关系 4.1.2二元关系的表示 1.用列举法表示二元关系 例4.1中的A到B的全域关系 E=A×B=a,1,a,2,b,1,b,2 A上的恒等关系 IA =a,a,b,b 都是用列举法表示的。 2.用描述法表示二元关系 设R是实数集，LR = x,y | xR∧yR∧x≤y， LR是 实数集R上的二元关系

第4章二元关系 3.用矩阵表示二元关系 如果A,B是有限集， A=a1,42,…,amy B=b1,b2,…,bn7, R是A到的二元关系，R的关系矩阵定义为： MR)nxn 1 ER 0 <abR i=1,…,mj=1,…,n 称为二元关系R的关系矩阵

第4章 二元关系 3.用矩阵表示二元关系 如果A，B是有限集， A=a1 ,a2 ,…,am ， B=b1 ,b2 ,…,bn ， R是A到B的二元关系，R的关系矩阵定义为： MR = mn R R b b a a r j j i i ij          = , , 0 1 i=1,…,m j=1,…,n 称为二元关系R的关系矩阵。 ( ) ij r

第4章二元关系 【例4.3】设Aa1,a2,4,a47,Bb1,b2,b3,R是A到B 的二元关系，定义为： R-,,,,,, 写出R的关系矩阵。 解：R的关系矩阵为： 1 1 1 MR 1 O 1 1

第4章 二元关系 【例4.3】设A=a1 ,a2 ,a3 ,a4 ，B=b1 ,b2 ,b3 ，R是A到B 的二元关系，定义为： R=a1 ,b1 ,a1 ,b3 ,a2 ,b2 ,a2 ,b3 ,a3 ,b1 ,a4 ,b1 ,a4 ,b2  写出R的关系矩阵。 解：R的关系矩阵为： MR =               1 1 0 1 0 0 0 1 1 1 0 1

第4章二元关系 【例4.4】设A1,2,3,4,R是A的二元关系，定义为： R=,,,,,,,7 写出A上二元关系R的关系矩阵 解：R的关系矩阵为： 1 0 0 M 1 1 1 例4.4中的二元关系R是A上的二元关系，只需看成A 到A的二元关系，利用上述定义，就可以方便地写出它 的关系矩阵。A上的二元关系和A到B的二元关系的关系 矩阵的定义是相同的

第4章 二元关系 【例4.4】设A=1,2,3,4，R是A的二元关系，定义为： R=1,1,1,2,2,1,3,2,3,1,4,3,4,2,4,1 写出A上二元关系R的关系矩阵。 解：R的关系矩阵为： MR =               1 1 1 0 1 1 0 0 1 0 0 0 1 1 0 0 例4.4中的二元关系R是A上的二元关系，只需看成A 到A的二元关系，利用上述定义，就可以方便地写出它 的关系矩阵。A上的二元关系和A到B的二元关系的关系 矩阵的定义是相同的

第4章二元关系 4.用图表示二元关系 如果A和B是有限集，R是A到B二元关系，还可以 用图表示二元关系R。表示二元关系R的图叫做R的关 系图。A到B二元关系的关系图和A上的二元关系的关 系图的定义是不一样的。分别描述如下： (I)A到B二元关系R的关系图 设A41,42,…,4nm},Bb1,b2,…,bn},R是A到B二 元关系，R的关系图的绘制方法如下： ①画出m个小圆圈表示A的元素，再画出n个小圆 圈表示B的元素。这些小圆圈叫做关系图的结点（下 同)。 ②如果∈R,则从a到b,画一根有方向（带箭 头)的线。这些有方向（带箭头）的线叫做关系图的边 (下同)

第4章 二元关系 4.用图表示二元关系 如果A和B是有限集，R是A到B二元关系，还可以 用图表示二元关系R。表示二元关系R的图叫做R的关 系图。A到B二元关系的关系图和A上的二元关系的关 系图的定义是不一样的。分别描述如下： ⑴A到B二元关系R的关系图 设A=a1 ,a2 ,…,am ，B=b1 ,b2 ,…,bn ，R是A到B二 元关系，R的关系图的绘制方法如下： ①画出m个小圆圈表示A的元素，再画出n个小圆 圈表示B的元素。这些小圆圈叫做关系图的结点(下 同)。 ②如果ai ,bj R，则从ai到bj画一根有方向(带箭 头)的线。这些有方向(带箭头)的线叫做关系图的边 (下同)

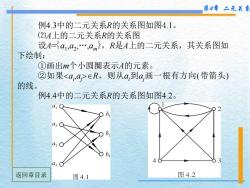
第4章二元关系 例4.3中的二元关系R的关系图如图4.1。 (2)A上的二元关系R的关系图 设A日a1,a,…,am,R是A上的二元关系，其关系图如 下绘 ①画出m个小圆圈表示A的元素。 ②如果∈R,则从a,到a,画一根有方向（带箭头） 的线。 例4.4中的二元关系R的关系图如图4.2。 a, b b3 3 返回章目录 图4.1 图4.2

第4章 二元关系 例4.3中的二元关系R的关系图如图4.1。 ⑵A上的二元关系R的关系图 设A=a1 ,a2 ,…,am ，R是A上的二元关系，其关系图如 下绘制： ①画出m个小圆圈表示A的元素。 ②如果ai ,aj R，则从ai到aj画一根有方向(带箭头) 的线。 例4.4中的二元关系R的关系图如图4.2。 返回章目录

第4章二元关系 4.2关系的运算 定义4.2.1设A,B是集合，RCAXB。 dom R=xx,>eR}叫做R的定义域。 ranR气)y∈R叫做R的值域。 FLDR=dom RUran R叫做R的域。 A叫做R的前域；B叫做R的陪域。 4.2.1二元关系的交、并、补、对称差运算 定理4.2.1设R,S是X到Y的二元关系，则RUS,R∩S, R-S,~R,R⊕S也是X到Y的二元关系。 证明：因为R,S是X到Y的二元关系，所以， RCYXY且SCYX Y。显然， RUSCX×Y,即RUS是X到Y的二元关系。 R∩SCYXY,即R∩S是X到Y的二元关系。 R-ScX×Y,即R-S是X到Y的二元关系

第4章 二元关系 4.2关系的运算 定义4.2.1设A，B是集合，RA×B。 dom R=x|x,yR  叫做R的定义域。 ran R=y| x,yR 叫做R的值域。 FLD R= dom R∪ran R叫做R的域。 A叫做R的前域；B叫做R的陪域。 4.2.1二元关系的交、并、补、对称差运算 定理4.2.1设R，S是X到Y的二元关系，则R∪S，R∩S， R-S，~R，R S也是X到Y的二元关系。 证明：因为R，S是X到Y的二元关系，所以， RX×Y且SX×Y。显然， R∪SX×Y，即R∪S是X到Y的二元关系。 R∩SX×Y，即R∩S是X到Y的二元关系。 R-SX×Y，即R-S是X到Y的二元关系。 