新疆大学：《工程力学》课程教学资源（习题指导）第9章 应力状态分析

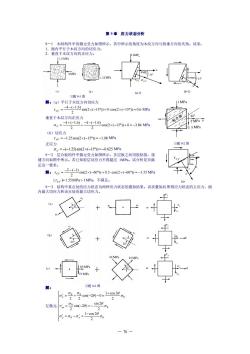
第9章应力状态分析 方向的正应力 习题91图 解：(a)平行于木纹方向切应力 Ty=4-1sin2x-15+0c0s2x-15=0.6MPs 垂直于木纹方向正应力 =4+16+4-1.cs2x15+0=-3.84MP (b)切应力 y■-1.25c0s(2x(-15)=-1.08MPa 正应力 习题92图 0635Mp 建动骨会纸种作电亮死层动智列不香资子园限路禁：提 足这一要求。 ：y=2-D,m2x6+05m2x(-609=-15MPg It=1.55MPa>IMPa,不满足， + ·+ 习2图 =9+号c0s(-20)-0=1+9s20 左微元-20=-20

— 78 — 习题 9-1 图 x  -15 x'  x' x' y'  1.25MP a  15 (b-1)  15 4MPa  -15 x' y'   x' x' 1.6MPa x (a-1) 习题 9-2 图 习题 9-2 图  y  x xy  =  y  x xy  = x  y  x xy  = x  30 2MPa 0.5MPa  -60  x' x' (a) x'y'  第 9 章 应力状态分析 9－1 木制构件中的微元受力如图所示，其中所示的角度为木纹方向与铅垂方向的夹角。试求： 1．面内平行于木纹方向的切应力； 2．垂直于木纹方向的正应力。 解：（a）平行于木纹方向切应力 sin(2 ( 15 )) 0 cos(2 ( 15 )) 0.6 2 4 ( 1.6)  −  +   −  = − − −  x  y  = MPa 垂直于木纹方向正应力 cos(2 ( 15 )) 0 3.84 2 4 ( 1.6) 2 4 ( 1.6)  −  + = − − − − + − + −  x  = MPa （b）切应力  x  y  = −1.25cos(2(−15)) = −1.08 MPa 正应力  x  = −(−1.25)sin(2(−15)) = −0.625 MPa 9－2 层合板构件中微元受力如图所示，各层板之间用胶粘接，接 缝方向如图中所示。若已知胶层切应力不得超过 1MPa。试分析是否满 足这一要求。 解： sin(2 ( 60 )) 0.5 cos(2 ( 60 )) 1.55 2 2 ( 1)  −  +   −  = − − − −  x  y  = MPa |  x  y  |= 1.55MPa  1 MPa，不满足。 9－3 结构中某点处的应力状态为两种应力状态的叠加结果。试求叠加后所得应力状态的主应力、面 内最大切应力和该点处的最大切应力。 解： 左微元          −  = −  =  = − = − +  = + − − = 0 0 0 0 0 0 0 2 1 cos 2 2 sin 2 sin( 2 ) 2 2 1 cos 2 cos( 2 ) 0 2 2                 y x xy x

a,-g.+a-3tcs200o 叠加w+029 口，-0，+0-l上29 2 +号ggi4学w 2 1=0 面内最大切应力：a-二2=s0 该点最大切应力：7m一；9_上g9。 左元iw5n2x30-夏0，0-0=-号0=6m2x(-309=号 右微元g-5n2x309-507-0-o2-9,-lm2x00》=-号 叠加,=o+o,=5r。,=o+o;=-50=rw+=0 01=V30,02=0,03=-5r0 面肉1上，0=5r 该点r上，=5r。 a.=0-[0+-0,0-30m2x45y-90Mp 叠加{o,=0+50-30)-10-10MPa b。=nr[-50al-M 拉}-9g兮网-0or40- 90 面内及该点：1Hn上.10-0-0Mp 9一4已知平而应力状态的最大正应力发生在与外力作用的自由表面AB相垂直的面上，其值为。· 试求应力分量a,、G,和t 黑：，=受+受c2x-2+0+c2a=,s'a 0,=0-0,=上cg20=0sm2a sm2x(-a-sim2a

— 79 — x A B  O  O   习题 (a) 9-4 图 A  60 B C  60 −100  x  x yx  xy  92MPa 习题 9-5 图 (a) 叠加          − =  + = = + = − + =  + =   0 0 0 0 2 1 cos 2 0 2 sin 2 0 2 3 cos 2              y y xy x y x x 0 (1 cos ) (1 cos ) ) 2 sin 2 ) 4( 2 1 cos 2 2 3 cos 2 ( 2 1 2 2 1 cos 2 2 3 cos 2 3 0 0 2 0 2 0 2 0 2 1 =    − + = + − − − +  − + + =                   面内最大切应力：      cos 2 0 1 2 max = −  = 该点最大切应力： 0 1 3 max 2 1 cos 2      + = − = 左微元 0 0 2 3   = −( )sin(2(−30)) =  x ， 0 2 3   = 0 −  = −  y x ， 2 cos(2 ( 30 )) 0 0    xy =  −  = 右微元 0 0 2 3   = −( )sin(230) =  x ， 0 2 3   = 0 −  = −  y x ， 2 ( ) cos(2 (30 )) 0 0    xy  = −   = − 叠加 3 0  = + =  x x y ， 3 0  = + = −  y y y ， xy =  xy +  xy  = 0 1 3 0  =  ， 2 = 0， 3 3 0  = −  面内 0 1 3 max 3 2 | |     = −  = 该点 0 1 3 max 3 2 | |     = − = 叠加            =       −  − − = + = + − − = =       −  − − + + − = + sin(2 ( 45 )) 30MPa 2 50 ( 30) 70 0 (50 30) 10 10MPa cos(2 ( 45 )) 90MPa 2 50 ( 30) 2 50 ( 30) 80 x y y x    主应力 0 0MPa 100MPa [90 (100)] 4 30 2 1 2 90 10 2 2 2 3 1 =     − +  = + =       面内及该点： 50 2 100 0 2 | | | | 1 3 max max = − = −  = =     MPa 9－4 已知平面应力状态的最大正应力发生在与外力作用的自由表面 AB 相垂直的面上，其值为  0 。 试求应力分量  x 、 y 和 xy  。 解：       2 0 0 0 cos 2 1 cos 2 cos(2 ( 2)) 0 2 2 = + x = +  − + =        2 0 0 0 sin 2 1 cos 2 = − y = − x =      sin 2 2 sin(2 ( )) 2 0 0 xy =  − = − α α

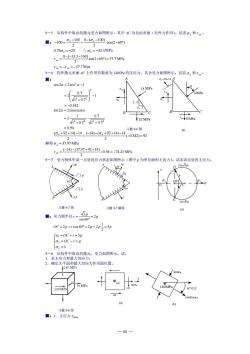
9一5从构件中取出的微元受力如图所示，其中4C为自由表面（无外力作用）.试求σ，和：， 解：-10=，10,0-a-100.cos2x60 2 a,=-33.3MPa t =-t=-577Mra 9一6构件微元表面4C上作用有数值为14MPa的压应力，其余受力如图所示。试求G,和：，。 解： cos2a=2cos'a-1 2 2F40F407 a,+2414-14,0-o,+92+10-40342=2 习题96图 (al 2 解得,=37.97MP -10-67n42+1山x094=-7425M 9一7受力物体中某一点处的应力状态知图所示（图中p为单位面积上的力）。试求该点处的主应力。 3 习题97图 习愿7解图 3p 解：应力圆半径r一品。-2p 0C=2p+rc0s60°-2p+2p-3p 「a,=OC+r=5p a;=0C-r=p 0,=0 9一8从构件中取出的微元，受力如图所示。试 大切应力作用面位置 140 MPa 120 MPa 习题9.8图 解：l.主应力rn

— 80 — 120 120 70MPa 140 x (a) 习题 9-6 图 14MPa 92MPa B C  x  +92+14 x xy  yx  A (a) 习题 9-7 图 A B 3 p 3 p  60 2p 2 p 习题 9-7 解图 习题 9-8 图  2 D C E O  1   120  (2p,− 3p) (2p, 3p) r (a) 140MPa 90MPa 160MPa( ) 1 36 52'12 o (b) 9－5 从构件中取出的微元受力如图所示，其中 AC 为自由表面（无外力作用）。试求  x 和 xy  。 解： cos(2 60 ) 2 0 ( 100) 2 100 100    − − + − − =  x  x 0.75 x = −25 ∴  x = −33.3 MPa sin(2 60 ) 57.7 2 0 [ 33.3 100]   = − − −  yx = MPa  xy = − yx = −57.7 Mpa 9－6 构件微元表面 AC 上作用有数值为 14MPa 的压应力，其余受力如图所示。试求  x 和 xy  。 解： 0.342 1 1 0.7 0.7 2 cos 2 2cos 1 2 2 2 2 = − −         + =  =  − 0.94 1 0.7 0.7 1 0.7 1 2 sin 2 2sin cos 2 2 2 2 = +  + =  =   ( 0.342) 92 2 ( 14) ( 92 14) 14 2 ( 92 14) 14 − = − − + + − +  x + + −  x 解得  x = 37.97 MPa 0.94 74.25 2 ( 14) (37.97 92 14)  = − − − + +  y x = MPa 9－7 受力物体中某一点处的应力状态如图所示（图中 p 为单位面积上的力）。试求该点处的主应力。 解：应力圆半径 p p r 2 sin 60 3 =  = OC p r p p 3p 2 1 = 2 + cos 60 = 2 + 2 =      = = − = = + = 0 5 3 2 1    OC r p OC r p 9－8 从构件中取出的微元，受力如图所示。试： 1．求主应力和最大切应力； 2．确定主平面和最大切应力作用面位置。 解：1．主应力 max 

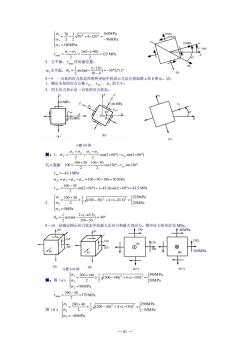
合-号miw 02=140MPa 7-,.10-←0.1sMa 2.主平面，作用面位置. o,主平面，=tam(-200)=-36°52'12 2.用主应力表示这一点处的应力状态。 150 MPa 习99图 解：1.-0+,cos2x60°)-t5im2×60y 代入数据100.00,0：0s120-a120 2 =-43.3MPa 0y=a,+a,-0=100+50-100=50MPa y-100,50sin2x60)+(43.3)cos2x60)-43.3MP 2. ，-流定相示发力秋态中的量大正位力经大国应力的年究没。 140 。” 150 (3) (b) =90MPa 、a.20+0±520-40+4x-50 (290MPa 图(b:{22 1-50MPa g3 =-90MPa 81

— 81 — (b) 习题 9-9 图  2 1 x  30 (c) (a) 150 140 300 90 (a-1) 140MPa 240MPa yx  (b-1) 40MPa 200MPa 150 90  8  45 35MPa  1 35MPa 125MPa 7'48'' x (c)      = − = + +  = 140MPa 90MPa 160MPa 70 4 120 2 1 2 70 2 2 2 3 1    125 2 160 ( 90) 2 1 3 max = − − = − =    MPa 2．主平面， max  作用面位置。  1 主平面， ) 36 52 12 70 0 2 120 arctan( 2 1 P = −    −   = − 9－9 一点处的应力状态在两种坐标中的表示方法分别如图 a 和 b 所示。试： 1．确定未知的应力分量 xy  、 x  y  、 y  的大小； 2．用主应力表示这一点处的应力状态。 解：1． cos(2 60 ) sin(2 60 ) 2 2   −   − + +  = x y x y x y x       代入数据  −  − + + = cos120 sin120 2 100 50 2 100 50 100 x y   xy = −43.3 MPa  y  = x + y − x  =100+50−100 = 50 MPa sin(2 60 ) ( 43.3) cos(2 60 ) 43.3 2 100 50   + −   = −  x  y  = MPa 2．      =     − +  − = + = 0MPa 25MPa 125MPa (100 50) 4 ( 43.3) 2 1 2 100 50 3 2 2 2 1    =  −  − = − ) 30 100 50 2 ( 43.3) arctan( 2 1  P 9－10 试确定图示应力状态中的最大正应力和最大切应力。图中应力的单位为 MPa。 习题 9-10 图 解：图（a）：      =     − +  − = + = 90MPa 50MPa 390MPa (300 140) 4 ( 150) 2 1 2 300 140 2 2 2 3 1    170 2 390 50 max = −  = MPa 图（b）：      = −    −  − +  − = + = 90MPa 50MPa 290MPa (200 40) 4 ( 150) 2 1 2 200 40 3 2 2 2 1   

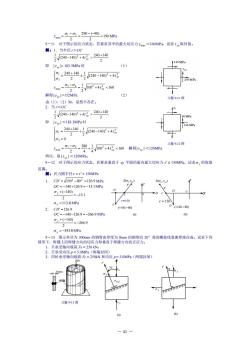
7-5;a.20-0-190Mm 9-11对于图示的应力状态，若要求其中的最大切应力O0 2240-140)2+45、240+140 2 即1E183.3MPa时 (1D 侣-g4号o 2 52-5m2+4城<10 解得1r<152MP (2) 由2，是然不存在。 7V240-1402+4r5≥240+140 2 即<183,3MPa时 -24010+240-140°+4 3=0 n-2.30+日om244<10解得1，<120MPa 习题912图 所以，取1t|<120MPa 9-12对于图示的应力状态，若要求垂直于y平面的面内最大切应力t≤1S0MPa,试求a,的取值 范 解：应力圆半径r=r'=150MP 1.CD°=1502-802=126.9MPa .t) 0C=-140+126.9=-13.1MP8 0,+140=-13. ,=I3.8MP 2. -140-80 (al ( 0,+140-2669 G,-393.8MPa 情形子不外的的信由方的20角的旋线卷曲焊接雨成。试求下列 承号轴载黄F。=50kN P=50MP(两端封闭)

— 82 — 习题 9-11 图 习题 9-12 图 习题 9-13 图  x 20 x'  y  y x (b)  20  x  x' x' y'   x x' x (a) x'y'  D' D O r  C ( . ) E y yx   (−140. −80) (−140. −80) D r = 150 C D' O   r ( , ) E y yx    (a) (b) r =150 190 2 290 ( 90) 2 1 3 max = − − = − =    MPa 9－11 对于图示的应力状态，若要求其中的最大切应力 max  ＜160MPa，试求 xy  取何值。 解：1．当半径 r＞OC 2 240 140 (240 140) 4 2 1 2 2 + − +  xy  即 | xy | 183.3MPa 时 （1）     − + + = 2 2 3 1 (240 140) 4 2 1 2 240 140 xy    100 4 160 2 1 2 1 3 2 2 max = +  − = xy     解得 | | xy  <152MPa （2） 由（1）、（2）知，显然不存在。 2．当 r＜OC 2 240 140 (240 140) 4 2 1 2 2 + − +  xy  即 | | xy  ＜183.3MPa 时      = + − + + = 0 (240 140) 4 2 1 2 240 140 3 2 2 1    xy 100 4 160 4 1 4 380 2 1 3 2 2 max = + +  − = xy     解得 | | xy  ＜120MPa 所以，取 | | xy  ＜120MPa。 9－12 对于图示的应力状态，若要求垂直于 xy 平面的面内最大切应力    150MPa，试求  y 的取值 范围。 解：应力圆半径 r =  = 150MPa 1． 150 80 126.9 2 2 CD = − = MPa OC = −140+126.9 = −13.1 MPa 13.1 2 ( 140) = −  y + −  y =113.8 MPa 2． CD =126.9 OC = −140−126.9 = −266.9 MPa 266.9 2 ( 140) = −  y + −  y = −393.8 MPa 9－13 图示外径为 300mm 的钢管由厚度为 8mm 的钢带沿 20°角的螺旋线卷曲焊接而成。试求下列 情形下，焊缝上沿焊缝方向的切应力和垂直于焊缝方向的正应力。 1．只承受轴向载荷 FP = 250 kN； 2．只承受内压 p = 5.0MPa（两端封闭） 3．同时承受轴向载荷 FP = 250kN 和内压 p = 5.0MPa（两端封闭）

解： 250x10 0w=-4072x2091-1095M a图a.-2-520-456M 0,-0-5g0-8.9125MR 5w-563,1255n2×20m)-146Mm -15649125,L56≥125w2×209=208Mp 5-156,9125gm2×209-256Ma 2 向正应力为OMPa,试求圆简承受的内压P, 解：tam0= =0.2 ,0-625p 习914图 62.5p+31252+625p-31.252os(20-90°)=0：=60 p= 4688-1563x028-1412MPm 知水的补果的为头杰A连接。下与系房B连接。已 2×11 03=0 7m=9,9_4085-0-2043MP 北v的数值。 第，055会o+0 两式相除 -83

— 83 —  y  x   x   − 90  y x' 习题 9 (a) -14 图 习题 9-15 图 解： （1）图 a： 34.07 π (300 8) 8 250 10 π 3 P =  −   = =   D F x MPa（压） cos(2 20 ) 30.09 2 34.07 2 34.07   = − − + −  x  = MPa sin(2 20 ) 10.95 2 34.07   = − −  x  y  = MPa （2）图 b： 45.63 4 8 5 (300 8) 4 =   − = =   pD x MPa 91.25 2 8 5 (300 8) 2 =   − = =   pD y MPa cos(2 20 ) 50.97 2 45.63 91.25 2 45.63 91.25   = − + +  x  = MPa sin(2 20 ) 14.66 2 45.63 91.25   = − −  x  y  = MPa （3）图 a、图 b 叠加：  x = 45.63−34.07 =11.56 MPa  y = 91.25 MPa cos(2 20 ) 20.88 2 11.56 91.25 2 11.56 91.25   = − + +  x  = MPa sin(2 20 ) 25.6 2 11.56 91.25   = − −  x  y  = MPa 所以也可（1）与（2）结果叠加得到。 9－14 图示的薄壁圆筒，由厚度为 8mm 的钢板制成，平均直径 1m。已知钢板表面上点 A 沿图示方 向正应力为 60MPa。试求圆筒承受的内压 p。 解： 4 3 tan = 0.28 ) 4 3 1 ( ) 4 3 1 ( 1 tan 1 tan cos 2 2 2 2 2 = + − = + − =    62.5 2 8 100 =   = p  x p 31.25 4 8 1000 =   = p  y p cos(2( 90 )) 60 2 62.5 31.25 2 62.5 31.25 −  = = − + + x  p p p p   1.412 46.88 15.63 0.28 60 = −  p = MPa 9－15 图示外径 D = 760mm、壁厚  = 11mm 的钢管，上端与蓄水池 A 连接，下端与泵房 B 连接。已 知水的密度  = 1000kg/m3。试求钢管在静态下的最大正应力与最大切应力。 解：管内内压 1000 9.8 122 10 1.20 6 = =    = − p gh MPa 40.85 2 11 1.20 (760 11) 1 =   −  =  环向 = MPa  3 = 0 20.43 2 40.85 0 2 1 3 max = − = − =    MPa 9－16 结构中某一点处的应力状态如图所示。试： 1．当  xy = 0， x = 200 MPa， y =100 MPa 时，测得由  x 、 y 引起的 x、y 方向的正应变分别为 3 2.42 10−  x =  ， 3 0.49 10−  y =  。求结构材料的弹性模量 E 和泊松比  的数值。 2．在上述所示的 E、v 值条件下，当切应力  xy = 80 MPa， x = 200 MPa， y =100 MPa 时，求 xy  。 解：（1） ( ) 1 ( ) 1 x y x y x y x y E v E v         − + − = + − + = 两式相除

-总-8调808s 解得r- 200+10 +) 687x10-257x10MP (2)G=20+02X+ E 习题9.16图 G=25.7×103 =3.1×10-3 9一17图示结构中，铝板的左边和下边被周定，上方与右方与刚性物体之间的间隙分别为△，= 0.75mm,A,=1.0mm.已知E=70GPa,v=0.33.a=24×106=/C.试求温升△M=40C和M=80C时 板中的最大切应力《假定板在自身平面内受力不发生弯曲). 解：(1)当△w=40 (W2-1,M:a=800×40x24×106-0.768mm△ Wy=600×80x24×10-6=1.152mm>A 习题917图 &,-800=4r-(W 02-g,月=A-( I 19, 9,-033g,=70x102×-536.19)=469 (1) 0g,-W9.-y-w 9,-0.34=70x103x152-075=469 所以解得 70-0-35MP 9一18对于一般平面应力状态，己知材料的弹性常数E、V,且由实验测得，和5，。试证明： 0,=E5+% -1 ,= :=+) 解：。，+0，名6，+G,) (1 0-0,6,-,) (2) 0+aa-倍普) -84

— 84 — 习题 9-16 图 习题 9-17 图 qy qx qy qx qx q y (a) 0.5 2.42 10 0.49 10 2.42 10 0.49 10 200 100 200 100 1 1 3 3 3 3 =  −   +   + − = − +  + − = + − − − − − x y x y x y x y           解得 3 1 r = 68.7 2.42 10 0.49 10 200 100 ) 3 1 (1 ( ) ( ) (1 ) 3 3 =  +  + = − + + = − − − x y x y E      MPa （2） 3 3 25.77 10 ) 3 1 2(1 68.7 10 2(1 ) =  +  = + =  E G MPa 3 3 3.1 10 25.77 10 80 − =   = = G xy xy   9－17 图示结构中，铝板的左边和下边被固定，上方与右方与刚性物体之间的间隙分别为  y = 0.75mm， x = 1.0mm。已知 E = 70GPa， = 0.33。 24 10 1/ 6  =  = − ℃。试求温升 t = 40℃和 t = 80℃时 板中的最大切应力（假定板在自身平面内受力不发生弯曲）。 解：（1）当 t = 40℃ ( ) 800 40 24 10 0.768 6  =   =    =  − l l x t  t x mm＜ x ( ) 600 40 24 10 0.576 6  =   =    =  − l l y t  t y mm＜ y 所以铝板内无温度应力，  max = 0 （2）当 t = 80℃ ( ) 800 80 24 10 1.536 6  =    = t − x l mm＞ x ( ) 600 80 24 10 1.152 6  =    = t − y l mm＞ y t x x x l   −800 =  − ( ) t x y x q q x l E  [− − (− )] =  − ( ) 800  ( ) 1 x x y v E  =  −  ∴ ) 46.9 800 1.536 1.0 0.33 70 10 ( 3 = − qx − qy =   （1） t y x y q q y l E  [− − (− )] =  − ( ) 600  ) 46.9 600 1.152 0.75 0.33 70 10 ( 3 = − qy − qx =   （2） 所以解得 qx = qy = 70MPa（压）  1 = 0， 2 = 3 = −70 MPa 35 2 0 ( 70) max = − −  = MPa 9－18 对于一般平面应力状态，已知材料的弹性常数 E、 ，且由实验测得 x  和 y  。试证明： 2 1     − + = x y x E 2 1     − + = y x y E ( ) 1 z x y      + − = − 解： ( ) 1 x y x y E      + − + = （1） ( ) 1 x y x y E      − + − = （2） （1）＋（2），         − + − = 2 2 1 2 1 2 2 v v v E x y x    （1）－（2），         − + − = 2 2 1 2 1 2 2 v v v E x y y   

=t,g,-6 e=-2a,+a,)=-6,+e,)=-6,+6,) 9一19图示构件在：方向上的正应变被限制为零，即6，=O。这时垂直这一方向上的截面保持平面 而且两相邻裁面间的距离保持不变，此即所滑平面应变问恩的一种。已知。，、。，和、，。试证明： c,=0-v2,-1+va, e,=20-2o,-w1+va1 解：，=0，a,-Ma,+a,月=0，所以o:=+o,) 8,=ax-a,+a,川 =5o,-o,+,)+o] -El-v)o,-vl+v)o,l 6,=eo,-Ma:+,月 习99国 =E(a,-Mv(a,+a,)+a.l =I0-2)a,-v0+v,1 9一20承受内压的铝合金制的圆筒形薄壁容器如图所示.已知内压P=35MPa,材料的E=75GPa, 0.33.试求圆筒的半径改变量。 ：7=35252476=5936MP 8=7,60 -3522470.72。 一螺栓 8-35ip7 -2+-. 2江r 角钢 习题920图 =华r=o-+0 09南 1OMPa时，液压缸内径的改变量。 解：缸体 液伍缸 Fr 径=-10MPa E-F 习题9-21图 4205Xo5-030-1030-2x2=265x10mm 9一22试证明对于一般应力状态，若应力应变关系保持线性，则应变比能 =a++a-2o,0,+0,0:+a:0,川+(+层+r) 解：应变比能0,6，+0,，+0：6+w++a7a(1) -85

— 85 — 习题 9-19 图 习题 9-20 图 习题 9-21 图 ∴ 2 1 v v E x y x − + =    ， 2 1 v v E y x y − + =    ( ) 1 ( ) 1 ( ) z x y x y x y E E E             + − + = − − = − + = −  9－19 图示构件在 z 方向上的正应变被限制为零，即 z  = 0。这时垂直这一方向上的截面保持平面， 而且两相邻截面间的距离保持不变，此即所谓平面应变问题的一种。已知  x 、 y 和 E、 。试证明： ( )  z =  x + y [(1 ) (1 ) ] 1 2 x x y E  = −  − +  [(1 ) (1 ) ] 1 2 y y x E  = −  − +  解： z  = 0， [ ( )] 0 1 z − x + y = E     ，所以 ( )  z =  x + y [(1 ) (1 ) ] 1 { [ ( ) ]} 1 [ ( )] 1 2 x y x x y y x x z y E E E                 = − − + = − + + = − + [(1 ) (1 ) ] 1 { [ ( ) ]} 1 [ ( )] 1 2 y x y x y x y y z x E E E                 = − − + = − + + = − + 9－20 承受内压的铝合金制的圆筒形薄壁容器如图所示。已知内压 p = 3.5MPa，材料的 E = 75GPa， = 0.33。试求圆筒的半径改变量。 解： 59.36 4 7.6 3.5 (254 2 7.6) =    +  轴 = MPa 118.72 2 7.6 3.5 (254 2 7.6) =    +  环 = MPa  径 = −3.5 MPa r r r r r r  = +  − = 2π 2π( ) 2π  环 [118.72 0.33(59.36 3.5)] 254 0.34mm 75 10 1 [ ( )] 1 3 − −  =  =  =  环  =  环 −  轴 + 径 E r r 9－21 液压缸及柱形活塞的纵剖面如图所示。缸体材料为钢，E = 205GPa， = 0.30。试求当内压 p = 10MPa 时，液压缸内径的改变量。 解：缸体上  轴 = 0 115 2 2 10 (50 4) =   −  环 = MPa  径 = −10 MPa [115 0.3(0 10)](50 2 2) 2.65 10 mm 205 10 1 2 3 − − − −  =   d内 = 9－22 试证明对于一般应力状态，若应力应变关系保持线性，则应变比能 ( ) 2 1 [ 2 ( )] 2 1 2 2 2 2 2 2 x y z x y y z z x x y y z zx E G v               = + + − + + + + + 解：应变比能 x x y y z z x y x y y z y z zx zx v              2 1 2 1 2 1 2 1 2 1 2 1 = + + + + + （1）

,=o,-,+,】 5,=Fo,-Ma:+o,月 广义胡克定律。 :=o:-a,+o, Yu-Gto :-GT (2)代入(1)得： "2Eo+a+a-2o,o,+a,a:+a:o,月+(r+r层+r) 9一23试求图a中所示的纯切应力状态旋转45°后各面上的应力分量，并将其标于图b中，然后 应用习愿9一2中的结果，分别计算图a和b两种情形下的应变比能，并令二者相等，从而证明： 解：a1a,o3=-0lo2=0 由(a)图 -2z0 由(b)图 =2E0D2+02+-2-21l0 习题923图 +0-(-+l- -" 两式相等之0oD2="0oD2G= E 1+V 9一24试证明主应力为0、2、的三向应力状态，其体积应变为 解：由广义胡克定律： 2=fo:-o+a】 ++6-l2产a+a+o 体积应变6=++12产a,+0+o 9一25关于用微元表示一点处的应力状态，有如下论述，试选择哪一种是正确的， 《A)微元形状可是是 （C)不一定是大而体 意的：能是六面体微 元，五面体微元也可以，其它形状侧不行： 上无形代可以是任意的。但上为的力分量足以任意方面上的力： -86

— 86 — 习题 9-23 图 广义胡克定律                  = = = = − + = − + = − + zx zx yz yz xy xy z z x y y y z x x x y z G G G E E E                      1 1 1 [ ( )] 1 [ ( )] 1 [ ( )] 1 （2） （2）代入（1）得： ( ) 2 1 [ 2 ( )] 2 1 2 2 2 2 2 2 x y z x y y z z x x y y z zx E G v               = + + − + + + + + 9－23 试求图 a 中所示的纯切应力状态旋转 45°后各面上的应力分量，并将其标于图 b 中。然后， 应用习题 9－22 中的结果，分别计算图 a 和 b 两种情形下的应变比能，并令二者相等，从而证明： 2(1+ ) = E G 解： | | 1 0  =  ， 1 | | 3 0  = −  ， 2 = 0 由（a）图 2 0 (| |) 2 1   G v = 由（b）图 [(| |) 0 ( | |) 2 | | 0 2 1 0 2 0 2 2 0 =  + + −  −     E v 0 ( | |) | | ( | |)] 0 0 0 +  −  +  −  2 0 (| |) 1   E + = 两式相等 2 0 2 0 (| |) 1 (| |) 2 1    G E + = ∴ 2(1+ ) = E G 9－24 试证明主应力为  1、 2 、 3 的三向应力状态，其体积应变为 ( ) 1 2  1  2  3    + + − = E 解：由广义胡克定律： [ ( )] 1 1  1   2  3  = − + E [ ( )] 1 2  2   3  1  = − + E [ ( )] 1 3  3   1  2  = − + E ( ) 1 2 1 2 3  1  2  3     + + − + + = E 体积应变 ( ) 1 2 1 2 3  1  2  3       + + − = + + = E 9－25 关于用微元表示一点处的应力状态，有如下论述，试选择哪一种是正确的。 （A）微元形状可以是任意的； （B）微元形状不是任意的，只能是六面体微元； （C）不一定是六面体微元，五面体微元也可以，其它形状则不行； （D）微元形状可以是任意的，但其上已知的应力分量足以确定任意方向面上的应力。 正确答案是 D

商的。一26对于国示承受轴向拉体的维形杆上的点太试用平街概念分析下列因种位力状态中雪一种是正 +A) 定应力互等定 (B)不清足平窗 应力互等，又能达到双向的平衡： D)不调足两个方向的平衡。 试根据不为等主应力 目，它是 单向应力状态 (D)纯切应力状态 50 正确答案是B 解：-0+009+50=10mMp a,-50+0-00+5302=0NMPa 习题927 ,=0,为单向应力状态 (B 等价 D和等价 P 5 架确答案是 (a图：a,=0,g,=0,tm=-7n (a （b)图：g,=o+-l+o-o)o2x459=0 5,=t0+(-t0)-g,=0 t,-n2x459=n ,=t0+(-0)-,=0 n-2x49=- 题928野 (d)图：,=-o,o,=r0,tg=0 9一29关于习题9一28图示的四个应力状态，有如下论述，试选择哪一种是正确的. 0 MP )其应变比能都相同。 解：园个应方力状态的主应力，=。、，=0、，=-10：其主力 高的虽不全相同。但应变比能与主应力值有关，因此它们的位变比能附 9一30关于图示应力状态，有如下论述，试选择哪一种是正确的， OMPa 应力为250MP 87

— 87 — 习题 9-26 图 习题 9-27 图 习题 9-28 图 习题 9-30 图 9－26 对于图示承受轴向拉伸的锥形杆上的点 A，试用平衡概念分析下列四种应力状态中哪一种是正 确的。 正确答案是 C 。 解：（A）不满足切应力互等定律； （B）不满足平衡； （C）既可满足切应力互等，又能达到双向的平衡； （D）不满足两个方向的平衡。 9－27 微元受力如图所示，图中应力单位为 MPa。试根据不为零主应力的数目，它是： （A）二向应力状态； （B）单向应力状态； （C）三向应力状态； （D）纯切应力状态。 正确答案是 B 。 解： ) 50 100 2 50 50 ( 2 50 50 2 2 1 + = − + +  = MPa ) 50 0 2 50 50 ( 2 50 50 2 2 2 + = − − +  = MPa  3 = 0 ，为单向应力状态。 9－28 试分析图示的四个应力状态是否等价，有下列四种答案。 （A）四者均等价； （B）仅（a）和（b）等价； （C）仅（b）、（c）等价； （D）仅（a）和（c）等价。 正确答案是 D 。 解： （a）图：  x = 0， y = 0 ， 0  = − xy （b）图： cos(2 45 ) 0 2 ( ) 2 ( ) 0 0 0 0   = − − + + − =      x  y = 0 +(− 0 ) − x = 0 0 0 0 sin(2 45 ) 2 ( )       = − − xy = （c）图： cos(2 45 ) 0 2 ( ) 2 ( ) 0 0 0 0   = − − + − + =      x  y = 0 +(− 0 ) − x = 0 0 0 0 sin(2 45 ) 2 ( )       = − − − xy = （d）图： 0  = − x ， 0  =  y ， xy = 0 9－29 关于习题 9－28 图示的四个应力状态，有如下论述，试选择哪一种是正确的。 （A）其主应力和主方向都相同； （B）其主方向都相同，主应力不同； （C）其主应力、主方向都不相同； （D）其应变比能都相同。 正确答案是 D 。 解：四个应力状态的主应力， 1 0  = 、 2 = 0 、 3 0  = − ；其主力 方向虽不全相同，但应变比能与主应力值有关，因此它们的应变比能相 同。 9－30 关于图示应力状态，有如下论述，试选择哪一种是正确的。 （A）最大主应力为 500MPa，最小主应力为 100MPa； （B）最大主应力为 500MPa，最大切应力为 250MPa；