新疆大学：《工程力学》课程教学资源（PPT课件）第五章 静力学原理应用于弹性杆

内力的概念 内力 ■ 物体因受外力作用而使其内部各部分之间 因相对位置改变而引起的相互作用力： ■材料力学中的内力，是指外力作用下，物 体各质点之间相互作用力的变化量，所以 是物体内部各部分之间因外力而引起的附 加相互作用力，即“附加内力”； ■内力随外力的增加而加大，随外力的撤除 而消失

内力的概念 ➢ 内力 ◼ 物体因受外力作用而使其内部各部分之间 因相对位置改变而引起的相互作用力； ◼ 材料力学中的内力，是指外力作用下，物 体各质点之间相互作用力的变化量，所以 是物体内部各部分之间因外力而引起的附 加相互作用力，即“附加内力” ； ◼ 内力随外力的增加而加大，随外力的撤除 而消失

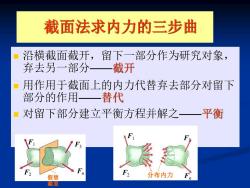
截面法求内力的三步曲 沿横截面截开，留下一部分作为研究对象， 弃去另 一部分一截开 用作用于截面上的内力代替弃去部分对留下 部分的作用 一替代 对留下部分建立平衡方程并解之一平衡 F 假想 分布内力 截面

截面法求内力的三步曲 ◼ 沿横截面截开，留下一部分作为研究对象， 弃去另一部分——截开 ◼ 用作用于截面上的内力代替弃去部分对留下 部分的作用——替代 ◼ 对留下部分建立平衡方程并解之——平衡 F1 F3 F2 Fn 假想 截面 F1 F2 F3 分布内力 Fn

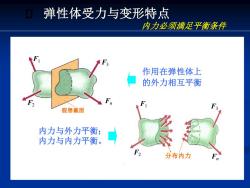
弹性体受力与变形特点 内力必须满足平衡条件 作用在弹性体上 的外力相互平衡 假想截面 内力与外力平衡； 内力与内力平衡。 分布内力

内力必须满足平衡条件 作用在弹性体上 的外力相互平衡 内力与外力平衡； 内力与内力平衡。 F1 F3 F2 Fn 假想截面 F1 F2 F3 分布内力 Fn 弹性体受力与变形特点

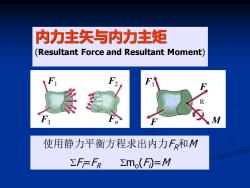
内力主矢与内力主矩 (Resultant Force and Resultant Moment) M 使用静力平衡方程求出内力F和M ΣF=FR >mo(F)=M

F1 F R F 3 M F1 F3 Fn F2 内力主矢与内力主矩 (Resultant Force and Resultant Moment) 使用静力平衡方程求出内力FR和M SFi=FR Smo (Fi )=M

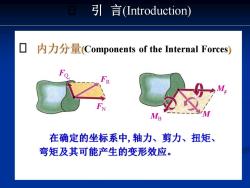
引言(Introduction) 内力分量(Components of the Internal Forces) M M 在确定的坐标系中，轴力、剪力、扭矩、 弯矩及其可能产生的变形效应

内力分量(Components of the Internal Forces) 在确定的坐标系中,轴力、剪力、扭矩、 弯矩及其可能产生的变形效应。 FR FN FQ M M B Mx 引 言(Introduction)

例1.1 确定m-m截面上的内力 N=P M-=Pa b a

例1.1 确定m-m截面上的内力 N=P M=Pa

例1直径为d长为1圆截面直杆，铅垂放置，上端 固定，若材料单位体积质量为P，试求因自重引起 杆的m-m截面的内力 o 解： 以2 q=P8- ∑F,=0, FN-gx=0 2 FN =qx- X 4 b) 以2 整个杆件最大的轴力发生 Fy-pe 在固定端截面上，其值： 4

整个杆件最大的轴力发生 在固定端截面上，其值： 例1 直径为 d 长为 l 圆截面直杆，铅垂放置，上端 固定，若材料单位体积质量为 ，试求因自重引起 杆的 m-m 截面的内力 。 解：

轴力图举例 一、 拉、压杆的内力nternal Forces】 【例1】求如图2~7所示杆件的内内，开作轴力图。 【解】 P=5kN =15kN,2 P-10kN (1)计剪各段内力 2)绘制轴力图 NikN) b P,=15kN 112 一一 (e) N-5kN N2=-10kN (d)

一、拉、压杆的内力(Internal Forces) 轴力图举例

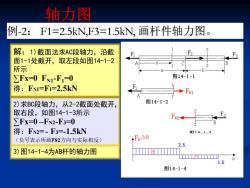
轴力图 例-2：F1=2.5kN,F3=1.5kN,画杆件轴力图。 解：1)截面法求AC段轴力，沿截 面1-1处截开，取左段如图14-1-2 所示 ∑Fx=0FN-F1=0 图14-1-1 得：FN1=F1=2.5kN 1 +F1 2)求BC段轴力，从2-2截面处截开， 图14-1-2 取右段，如图14-1-3所示 2 F3 ∑Fx=0-FN2-F3=0 得：F2=-F3=-1.5kN 凤1-1-2 (负号表示所画FN2方向与实际相反) Fx/kN 2.5 3)图14-1-4为AB杆的轴力图 1.5 图14-1-4

轴力图 例-2： F1=2.5kN,F3=1.5kN, 画杆件轴力图。 解：1)截面法求AC段轴力，沿截 面1-1处截开，取左段如图14-1-2 所示 ∑Fx=0 FN1-F1=0 得：FN1=F1=2.5kN 2)求BC段轴力，从2-2截面处截开， 取右段，如图14-1-3所示 ∑Fx=0 –FN2-F3=0 得：FN2= - F3=-1.5kN （负号表示所画FN2方向与实际相反） 3)图14-1-4为AB杆的轴力图

轴力图举例 例题2-3 11 B 12 c 3 D 已知F=10kN;F)=20kN; F3=35kWN;F25kN;试画 F 出图示杆件的轴力图。 1F22F3 解：1、计算各段的轴力。 →Fw AB段 ∑F=0 FNI=F=10kN -FN2 BC段 F2 ∑F=0F2+E=F FN2=F-F2= 10-20=-10kN F (kN) 10 CD段 ∑F=0 FN3 F =25kN 2、绘制轴力图

已知F1=10kN；F2=20kN； F3=35kN；F4=25kN;试画 出图示杆件的轴力图。 1 1 Fx = 0 FN1 = F1 =10kN 例题2-3 FN1 F1 解：1、计算各段的轴力。 F1 F2 F3 F4 A B C D AB段 10 20 10kN 2 1 2 − = − FN = F − F = BC段 2 2 3 3 FN3 F4 FN2 F1 F2 Fx = 0 FN2 + F2 = F1 Fx = 0 FN3 = F4 = 25kN CD段 2、绘制轴力图。 (kN) FN x 10 25 10 (+) (−) (+) 轴力图举例