《结晶学与矿物学》课程教学资源（步进教程，PPT课件）05 晶体内部结构和生长简介

5晶体内部结构和生长简介

5 晶体内部结构 和生长简介

第一节 14种布拉维空间格子一、平行六面体的选取原则①所选取的平行六面体应能反映结点分布整体所固有的对称性；在上述前提下，所选取的平行六面体中棱与棱之间的直角20关系力求最多：在满足以上两条件的基础上，所选取的平行六面体的体积力求最小。O福即尽量使a=b=c，α=β=y=90°O?20O8300O按上述原则，.1选取的平行六面体最合理54O?

第一节 14种布拉维空间格子 • 一、平行六面体的选取原则 ① 所选取的平行六面体应能反映结点分布整体所固有的对称 性； ② 在上述前提下，所选取的平行六面体中棱与棱之间的直角 关系力求最多； ③ 在满足以上两条件的基础上，所选取的平行六面体的体积 力求最小。 即尽量使a＝b＝c，α＝β ＝ γ＝90° 。 按上述原则， 1选取的平行六面体最合理

二、空间格子类型1．根据格子常数特点，划分的空间格子类型等轴格子：a=b=c；α=β=y=90°四方格子：a=bc；α=β=y=90°六方格子：a=b#c；α=β=90°，y=120三方格子：a=b=c；α=β=y#90°，斜方格子：a#b±c；α=β=y=90°单斜格子：a#b±c；α=y=90°，β90三斜格子：a#bc；a#y+90°

二、空间格子类型 1. 根据格子常数特点，划分的空间格子类型 • 等轴格子：a＝b＝c；α＝β＝γ＝90° • 四方格子：a＝b≠c；α＝β＝γ＝90° • 六方格子：a＝b≠c；α＝β＝90° ，γ＝120° • 三方格子：a＝b＝c；α＝β＝γ≠90° ， • 斜方格子：a≠b≠c；α＝β＝γ＝90° • 单斜格子：a≠b≠c；α＝γ＝90° ，β≠90° • 三斜格子：a≠b≠c；α≠β≠γ≠90°

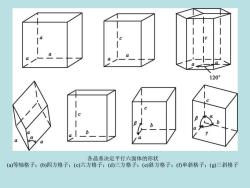
C1120°各晶系决定平行六面体的形状(a)等轴格子；(b)四方格子（c)六方格子；(d）三方格子；（e)斜方格子；(f)单斜格子；（g）三斜格子

各晶系决定平行六面体的形状 (a)等轴格子；(b)四方格子；(c)六方格子；(d)三方格子；(e)斜方格子；(f)单斜格子；(g)三斜格子

，2.根据结点的分布位置，划分的空间格子类型①原始格子（P）一一结点分布于平行六面体的8个角顶上②底心格子一一结点分布于平行六面体的角顶及某一对面的中心。其中，根据面中心点的位置特点又可细分为：C心格子，即结点分布于平行六面体的角顶和垂直于Z轴的一对面的中心：A心格子，即结点分布于平行六面体的角顶垂直X轴的一对面的中心：B心格子，即结点分布于平行六面体的角顶和垂直Y轴的一对面的中心。一般情况下称谓的底心格子指的是C心格子③体心格子（ID一一结点分布于平行六面体的角顶和体中心。④面心格子（F）一一结点分布于平行六面体的角顶和三对面的中心

• 2. 根据结点的分布位置，划分的空间格子类型 • ①原始格子（P）—— 结点分布于平行六面体的8个角顶上。 • ②底心格子 —— 结点分布于平行六面体的角顶及某一对 面的中心。其中，根据面中心点的位置特点又可细分为： C心格子，即结点分布于平行六面体的角顶和垂直于Z轴的一 对面的中心； A心格子，即结点分布于平行六面体的角顶垂直X轴的一对面 的中心； B心格子，即结点分布于平行六面体的角顶和垂直Y轴的一对 面的中心。 一般情况下称谓的底心格子指的是C心格子。 • ③体心格子（I）—— 结点分布于平行六面体的角顶和体 中心。 • ④面心格子（F）—— 结点分布于平行六面体的角顶和三 对面的中心

C空间格子的4种基本类型(a）原始格子；（b)底心格子（C心）；（c)底心格子（A心）；(d)底心格子（B心）；（e）体心格子；（f)面心格子

空间格子的4种基本类型 (a)原始格子；(b)底心格子（C心）；(c)底心格子（A心）； (d)底心格子（B心）；(e)体心格子；(f)面心格子

3：十四种布拉维格子按晶格常数7种平行六面体按结点位置4种类型格子是否有7×4=28种空间格子？答案是否定的。因为在这28种中，某些类型的格子彼此重复并可转换，还有一些不符合某晶系的对称特点而不能在该晶系中存在，因此，只有14种空间格子，也叫14种布拉维格子（A.Bravais于1848年最先推导出来的）

3．十四种布拉维格子 按晶格常数——7种平行六面体 按结点位置——4种类型格子 是否有7×4=28种空间格子？ 答案是否定的。因为在这28种中，某些类型的格 子彼此重复并可转换，还有一些不符合某晶系的 对称特点而不能在该晶系中存在，因此,只有14 种空间格子，也叫14种布拉维格子。 （A.Bravais于1848年最先推导出来的）

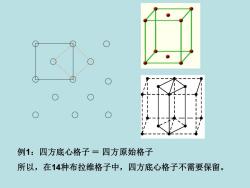
例1：四方底心格子三四方原始格子所以，在14种布拉维格子中，四方底心格子不需要保留

例1：四方底心格子 ＝ 四方原始格子 所以，在14种布拉维格子中，四方底心格子不需要保留

例2：立方底心格子不符合等轴晶系对称特点？因为立方底心格子不具4L3，所以，在14种布拉维格子中，立方底心格子不存在

例2：立方底心格子不符合等轴晶系对称特点？ 因为立方底心格子不具4L3 ，所以，在14种布拉维格子中 ，立方底心格子不存在

例3：三方面心格子（虚线）三三方原始格子（实线）

• 例3：三方面心格子（虚线）＝ 三方原始格子（实线）