香港中文大学：《Probability and Statistics for Engineers》课程教学资源（课件讲稿）General random variables

NGG430Protaistics fonr Chapter 3:General Random Variables Instructor:Shengyu Zhang

Instructor: Shengyu Zhang

Content Continuous Random Variables and PDFs Cumulative Distribution Functions Normal Random Variables Joint PDFs of Multiple Random Variables Conditioning The Continuous Bayes'Rule

Content  Continuous Random Variables and PDFs  Cumulative Distribution Functions  Normal Random Variables  Joint PDFs of Multiple Random Variables  Conditioning  The Continuous Bayes’ Rule

Continuous Random Variables We've learned discrete random variables, which can be used for dice rolling,coin flipping,etc. Random variables with a continuous range of possible values are quite common. velocity of a vehicle traveling along the highway Continuous random variables are useful: finer-grained than discrete random variables able to exploit powerful tools from calculus

Continuous Random Variables  We’ve learned discrete random variables, which can be used for dice rolling, coin flipping, etc.  Random variables with a continuous range of possible values are quite common.  velocity of a vehicle traveling along the highway  Continuous random variables are useful:  finer-grained than discrete random variables  able to exploit powerful tools from calculus

Continuous r.v.and PDFs A random variable X is called continuous if there is a functionfx =0,called the probability density function of X,or PDF,s.t. P(X∈B)=fx(x)dx R for every subset B R. We assume the integral is well-defined Compared to discrete case:replace summation by integral

Continuous r.v. and PDFs  A random variable 𝑋 is called continuous if there is a function 𝑓𝑋 ≥ 0, called the probability density function of 𝑋, or PDF, s.t. 𝑃 𝑋 ∈ 𝐵 = 𝑓𝑋 𝑥 𝑑𝑥 𝐵 for every subset 𝐵 ⊆ ℝ.  We assume the integral is well-defined.  Compared to discrete case: replace summation by integral

PDF In particular,when B [a,b], b pa≤X≤b)=x(x)dx is the area under the graph of PDF. PDF fx(x) Sample space b Event as Xsb}

PDF  In particular, when 𝐵 = 𝑎, 𝑏 , 𝑃 𝑎 ≤ 𝑋 ≤ 𝑏 = 𝑓𝑋 𝑥 𝑑𝑥 𝑏 𝑎 is the area under the graph of PDF

PDE ■P(a≤X≤a)=∫%fx(x)dx=0. P(a≤X≤b)=P(a<X≤b) =P(a≤X<b)=P(a<X<b) The entire area under the graph is equal to 1. 00 fx(x)dx=P(-oo≤X≤o)=1 -00 PDF fx(a) Sample space Event{a≤Xsb)

PDF  𝑃 𝑎 ≤ 𝑋 ≤ 𝑎 = 𝑓𝑋 𝑥 𝑑𝑥 𝑎 𝑎 = 0. ∴ 𝑃 𝑎 ≤ 𝑋 ≤ 𝑏 = 𝑃 𝑎 < 𝑋 ≤ 𝑏 = 𝑃 𝑎 ≤ 𝑋 < 𝑏 = 𝑃 𝑎 < 𝑋 < 𝑏  The entire area under the graph is equal to 1. 𝑓𝑋 𝑥 𝑑𝑥 ∞ −∞ = 𝑃 −∞ ≤ 𝑋 ≤ ∞ = 1

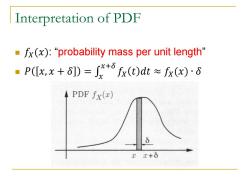
Interpretation of PDF ·fx(x):“probability mass per unit length” ■P(lx,x+D=+fx()at≈fr(x)G PDF fx(x) xE+δ

Interpretation of PDF  𝑓𝑋(𝑥): “probability mass per unit length”  𝑃 𝑥, 𝑥 + 𝛿 = 𝑓𝑋 𝑡 𝑑𝑡 𝑥+𝛿 𝑥 ≈ 𝑓𝑋(𝑥) ∙ 𝛿

Example 1:Uniform Consider a random variable X takes value in interval a,b]. Any subintervals of the same length have the same probability. It is called uniform random variable

Example 1: Uniform  Consider a random variable 𝑋 takes value in interval 𝑎, 𝑏 .  Any subintervals of the same length have the same probability.  It is called uniform random variable

Example 1:Uniform Its PDF has the form ifa≤x≤b otherwise PDF fx(x) 1 b-a 0 b

Example 1: Uniform  Its PDF has the form 𝑓𝑋 𝑥 = 1 𝑏 − 𝑎 , if 𝑎 ≤ 𝑥 ≤ 𝑏 0, otherwise

Example 2:Piecewise Constant When sunny,driving time is 15-20 minutes. When rainy,driving time is 20-25 minutes. With all times equally likely in each case. Sunny with prob.2/3,rainy with prob.1/3 The PDF of driving time X is C1, if15≤x≤20 fx(x)= C2, if20≤x≤25 0, otherwise

Example 2: Piecewise Constant  When sunny, driving time is 15-20 minutes.  When rainy, driving time is 20-25 minutes.  With all times equally likely in each case.  Sunny with prob. 2/3, rainy with prob. 1/3  The PDF of driving time 𝑋 is 𝑓𝑋 𝑥 = 𝑐1, if 15 ≤ 𝑥 ≤ 20 𝑐2, if 20 ≤ 𝑥 ≤ 25 0, otherwise