香港中文大学：《Probability and Statistics for Engineers》课程教学资源（辅导材料）Tutorial 2：Sample Space and Probability 2

Tutorial 2:Sample Space and Probability 2 Baoxiang WANG bxwang@cse Spring 2017

Tutorial 2: Sample Space and Probability 2 Baoxiang WANG bxwang@cse Spring 2017

Probability models A probability model is an assignment of probabilities to every element of the sample space. Probabilities are nonnegative and add up to one. Examples S=HH,HT,TH,TT /4/44/4 models a pair of coins with equally likely outcomes

Probability models A probability model is an assignment of probabilities to every element of the sample space. Probabilities are nonnegative and add up to one. S = { HH, HT, TH, TT } ¼ ¼ ¼ ¼ Examples models a pair of coins with equally likely outcomes

Elements of a Probabilistic Model Event:a subset of sample space. -A is a set of possible outcomes -Example.A ={HH,TT},the event that the two coins give the same side. The probability law assigns our knowledge or belief to an event Aa number P(A)>0. It specifies the likelihood of any outcome

Elements of a Probabilistic Model • Event: a subset of sample space. – 𝐴 ⊆ Ω is a set of possible outcomes – Example. 𝐴 = 𝐻𝐻, 𝑇𝑇 , the event that the two coins give the same side. • The probability law assigns our knowledge or belief to an event 𝐴 a number 𝑃 𝐴 ≥ 0. – It specifies the likelihood of any outcome

Probability Axioms 1.(Non-negativity)P(A)>0,for every event A. 2.(Additivity)For any two disjoint events A and B,P(AUB)=P(A)+P(B) In general,if A1,A2,..are disjoint events, then P(A1UA2U…)=P(A1)+P(A2)+… 3.(Normalization)P()=1

Probability Axioms 1. (Non-negativity) 𝑃(𝐴) ≥ 0, for every event 𝐴. 2. (Additivity) For any two disjoint events 𝐴 and 𝐵, 𝑃 𝐴 ∪ 𝐵 = 𝑃 𝐴 + 𝑃 𝐵 In general, if 𝐴1 , 𝐴2 , … are disjoint events, then 𝑃 𝐴1 ∪ 𝐴2 ∪ ⋯ = 𝑃 𝐴1 + 𝑃 𝐴2 + ⋯ 3. (Normalization) 𝑃(Ω) = 1

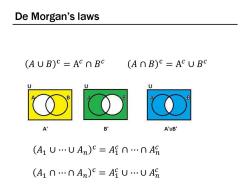
De Morgan's laws AUB)C=AcnBC (AnB)=ACUBC U U B A B' A'uB' (A1UUAn)c=An…nA9 (A1n…nAn)c=AUUA

De Morgan’s laws 𝐴 ∪ 𝐵 c = A 𝑐 ∩ 𝐵 𝑐 𝐴 ∩ 𝐵 c = A 𝑐 ∪ 𝐵 𝑐 𝐴1 ∪ ⋯ ∪ 𝐴𝑛 c = 𝐴1 𝑐 ∩ ⋯ ∩ 𝐴𝑛 𝑐 𝐴1 ∩ ⋯ ∩ 𝐴𝑛 c = 𝐴1 𝑐 ∪ ⋯ ∪ 𝐴𝑛 𝑐

Question Bonferroni's inequality. Prove that for any two events a and B,we have P(A∩B)≥P(A)+P(B)-1 P(A)+P(B)-P(AnB)=P(AUB) P(AUB)≤1 A AnB B

Question Bonferroni’s inequality. Prove that for any two events A and B, we have 𝑃 𝐴 ∩ 𝐵 ≥ 𝑃 𝐴 + 𝑃 𝐵 − 1 𝑃 𝐴 + 𝑃 𝐵 − 𝑃 𝐴 ∩ 𝐵 = 𝑃(𝐴 ∪ 𝐵) 𝑃(𝐴 ∪ 𝐵) ≤ 1

Question Romeo and Juliet have a date. Each will arrive at the meeting place with a delay between 0 and 1 hour,with all pairs of delays being equally likely. The first to arrive will wait for 15 minutes and will leave if the other has not yet arrived. Question:What is the probability that they will meet?

Question Romeo and Juliet have a date. Each will arrive at the meeting place with a delay between 0 and 1 hour, with all pairs of delays being equally likely. The first to arrive will wait for 15 minutes and will leave if the other has not yet arrived. Question: What is the probability that they will meet?

Question Sample space:the unit square[0,1]×[0,1], Its elements are the possible pairs of delays. 1/4 "equally likely"pairs of delays:let P(A)for event 1/4 A∈be equaltoA's& "area”. M={x0:x-川≤，0≤x≤1,0≤y≤1 This satisfies the axioms

Question Sample space: the unit square 0,1 × 0,1 , Its elements are the possible pairs of delays. “equally likely” pairs of delays: let 𝑃 𝐴 for event 𝐴 ⊆ Ω be equal to 𝐴’s “area”. This satisfies the axioms. 𝑀 = 𝑥, 𝑦 : 𝑥 − 𝑦 ≤ 1 4 , 0 ≤ 𝑥 ≤ 1, 0 ≤ 𝑦 ≤ 1

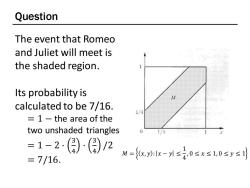
Question The event that Romeo and Juliet will meet is the shaded region. Its probability is calculated to be 7/16. 1/4 1-the area of the two unshaded triangles 1/4 =1-2)(国)2 =7/16. M={x,0lx-1≤40≤x≤1,0≤y≤1

Question The event that Romeo and Juliet will meet is the shaded region. Its probability is calculated to be 7/16. = 1 − the area of the two unshaded triangles = 1 − 2 ⋅ 3 4 · 3 4 /2 = 7/16. 𝑀 = 𝑥, 𝑦 : 𝑥 − 𝑦 ≤ 1 4 , 0 ≤ 𝑥 ≤ 1, 0 ≤ 𝑦 ≤ 1

Question A parking lot contains 100 cars,k of which happen to be lemons.We select m of these cars at random and take them for a test drive.Find the probability that n of the cars tested turn out to be lemons. The sample space frandom choose m cars The size of sample space =(）

Question A parking lot contains 100 cars, 𝑘 of which happen to be lemons. We select 𝑚 of these cars at random and take them for a test drive. Find the probability that 𝑛 of the cars tested turn out to be lemons. The sample space Ω = random choose 𝑚 cars The size of sample space |Ω| = 100 𝑚