西安电子科技大学：《电动力学 Electrodynamics》课程教学资源（课件讲稿）第0章 矢量分析 Vector analysis

Xidian University 本章内容 §0.1矢量代数(vector analysis) §0.2微分(differential calculus) §0.3积分(integral calculus) §0.4曲线坐标系(curvilinear coordinates) §0.5 Delta函数(The Dirac Delta function) §0.6矢量场论(Theory of vector fields) 西安电子科技大学学

西安电子科技大学2 §0.1 矢量代数（vector analysis） 本章内容 §0.2 微分（differential calculus） §0.3 积分（integral calculus） §0.4 曲线坐标系（curvilinear coordinates） §0.5 Delta 函数（The Dirac Delta function） §0.6 矢量场论（Theory of vector fields）

Xidian University §0.I矢量代数 一、矢量运算 标量：只有大小没有方向的物理量。如：质量，电荷等。 矢量：既有大小又有方向的物理量。如：速度，场强等。 矢量几何表示：有大小有方向的线段 矢量代数表示： A=0A=EA 大小： 4= 单位矢量： ēA二 A 矢量的几何表示 常矢量：大小和方向均不变的矢量。 注意：单位矢量不一定是常矢量。 西安电子科技大学

西安电子科技大学 §0.1 矢量代数 一、矢量运算 大小： A A  单位矢量： 标量：只有大小没有方向的物理量。如：质量，电荷等。 A A e A  矢量代数表示： A e A e A   A A 矢量：既有大小又有方向的物理量。如：速度，场强等。 矢量几何表示：有大小有方向的线段 注意：单位矢量不一定是常矢量。 A 矢量的几何表示 常矢量：大小和方向均不变的矢量

Xidian University 1.矢量的加减)法 交换律(commutative) 4+B=B+4 结合律(associative) A+(B+C)=(A+B)+C 矢量的加法 2.标量乘矢量 分配律(distributive) a(A+B)=aA+aB B -B 3.矢量的点积(dot product), 4.B=ABcos0 矢量的减法 4.B=B.A 交换律 4.(B+C)=4.B+4.C B 分配率 1.7=7=4 矢量A与B的夹角 西安电子科技大学

西安电子科技大学 1.矢量的加(减)法 矢量的加法 A B    A B   矢量的减法 A B    A  B  B   结合律(associative) A B C A B C      ( ) ( ) 交换律(commutative) A B B A  2.标量乘矢量 3.矢量的点积（dot product）    ( ) A B A B    A B B A    交换律 A B   矢量 A 与 的夹角  B  q A B AB   cosq A B C A B A C （    + ）= 分配率 2 2 A A A A    分配律(distributive)

Xidian University 4.矢量的矢积(cross product) Ax B=e,ABsin0 A×B 4xB=-BxA B AB sin 6 Ax(B+C)=A×B+AxC A A×A=0 矢量A与B的叉积 若A上B,则 A×B=AB 若A11B,则 A×B=0 西安电子科技大学

西安电子科技大学 若 ，则 若 ，则 4.矢量的矢积（cross product） sin A B e AB   n q A B B A     A B  A B AB   A B / / A B  0 q AB sin q A B    B  A  矢量 A 与 的叉积  B  A B C A B A C      ( + ) A A  0

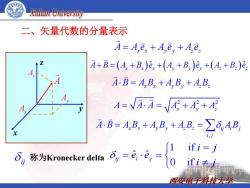
Xidian University 二、矢量代数的分量表示 A=A,e,+A,e,+A.e. A+B=(4,+B,)e,+(A,+B)e,+(A.+B.)2. A·B=AB+A,B,+AB 4=v7=+4+4 AB=A,B+A,B,+AB.=∑δ4，B i. ifi=j δ 称为Kronecker delta( 01-e =8 fi≠j 西安电子科技大学

西安电子科技大学 A A e A e A e    x x y y z z 222 A A A A A A      x y z 二、矢量代数的分量表示 z Ax  A Ay Az x y A B A B A B A B x x y y z z       ˆ   ˆ   ˆ A B A B e A B e A B e        x x x y y y z z z , x x y y z z ij i j i j A B A B A B A B A B        ij 称为Kronecker delta 1 if ˆ ˆ 0 if ij i j i j e e i j         

Xidian University 矢量的矢积的分量表示 AxB=e,(A,B.-AB,)+,(A.B,-AB:)+e.(A,B,-A,B:) 写成行列式形式为 e, e, AxB= A. A A ∑EkAB, = B B、 B i,ik A×B €k B 称为Levi-Civita symbol AB sin 0 1 ifk=123231,312 A -1 ifk=132,213,321 矢量A与B的叉积 0 otherwise 西安电子科技大学

西安电子科技大学 7 矢量的矢积的分量表示 ( ) ( ) ( ) A B e A B A B e A B A B e A B A B        x y z z y y z x x z z x y y x , , x y z x y z ijk i j k i j k x y z e e e A B A A A A B e B B B     写成行列式形式为 q AB sin q A B    B  A  矢量 A 与 的叉积  B  ijk  称为Levi-Civita symbol 1 if =123,231,312 1 if =132,213,321 0 otherwise ijk ijk  ijk      

Xidian University 三、矢量的三重积 l.标量三重积(scalar triple product) A:(B×C)=B(C×A)=C(A×B) 2.矢量三重积(vector triple product) 4x(BxC)=B(4.C)-C(4.B) BAC-CAB rule Ax(BxC)≠(4×B)xC not associative 例：利用BAC-CAB rule证明 A×(B×C)+Bx(C×d+C×(AxB)=O 西安电子科技大学

西安电子科技大学 三、矢量的三重积 A B C B C A C A B         ( ) ( ) ( ) A B C B A C C A B       ( ) ( ) ( ) 1.标量三重积（scalar triple product） 2.矢量三重积（vector triple product） A B C A B C      ( )   not associative BAC-CAB rule 例：利用BAC-CAB rule 证明 A B C B C A C A B       ( )+ ( )+ ( )=0

Xidian University 四、位矢、场点、源点 位置矢量 r=xex yey zez ”=|时=VF.示=√x2+y2+之 er r/r 源点 exe,=e,·e=e·ex=0 场点 exex=e,·e,=eE.=l 间距矢量 R=-'=(x-x)e+(y-y）)ey+(z-2)e 西安电子科技大学

西安电子科技大学 0 x y y z z x 源点 r  e e e e e e       四、位矢、场点、源点 场点 r 1 x x y y z z e e e e e e      

Xidian University §O.2微分(differential calculus) 一、梯度(gradient) 梯度是个矢量 VT- 8x ay 02 全微分 dT 8dd+0测 8x ∂Idy+ aT dz =(VT)·(di)=VTdI cos0 几何意义： 梯度VT的方向指向函数T的最大变化率（方向导数）方 向，其大小即为函数T的最大变化率（方向导数）。 西安电子科技大学

西安电子科技大学 §0.2 微分（differential calculus） 一、梯度（gradient）

Xidian University 例：求梯度，已知r=问=[(x-x+0-y+(-)] Vr=? Ox 20x-0=-￥ 2r y-y'or z-z' ay vr-ex-xey-ytoi 下 r 下 Yr= r 西安电子科技大学

西安电子科技大学 例：求梯度，已知       1 2 2 2 2 r r x x y y z z               r=？ 1 1 2( ) 2 r x x x x x r r          , r y y r z z y r z r           x y z x x y y z z r r e e e r r r r             解： = ˆ r r r r  