电子科技大学：《振动理论与声学原理 Vibration and Acoustics》课程教学资源（课件讲稿）第四章 多自由度系统的振动

振动理论与声学原理 第四章多自由度系统的振动 于亚婷 E-mail:wzwyyt@uestc.edu.cn Office address:主楼C1302 电子科技大学机械与电气工程学院

1 第四章 多自由度系统的振动 于亚婷 E-mail: wzwyyt@uestc.edu.cn Office address:主楼C1302 电子科技大学.机械与电气工程学院

课堂讨论主题4： 口主题：振动事故分析要求每组调研国内外 振动事故案例，分析事故原因，提出改进 措施。 口时间：10月18日周五（10-11) 口课堂PPT交流讨论，每组至少15分钟。 2

2 p 时间：10月18日 周五（10-11） p 课堂PPT交流讨论，每组至少15分钟

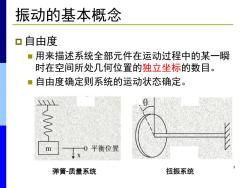
振动的基本概念 自由度 用来描述系统全部元件在运动过程中的某一瞬 时在空间所处几何位置的独立坐标的数目。 自由度确定则系统的运动状态确定。 m 0平衡位置 弹簧-质量系统 扭振系统

3 振动的基本概念 p 自由度 n 用来描述系统全部元件在运动过程中的某一瞬 时在空间所处几何位置的独立坐标的数目。 n 自由度确定则系统的运动状态确定。 弹簧-质量系统 扭振系统

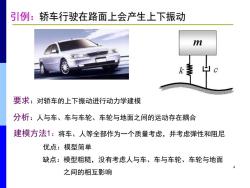
引例：轿车行驶在路面上会产生上下振动 m 要求：对轿车的上下振动进行动力学建模 分析：人与车、车与车轮、车轮与地面之间的运动存在耦合 建模方法1：将车、人等全部作为一个质量考虑，并考虑弹性和阻尼 优点：模型简单 缺点：模型粗糙，没有考虑人与车、车与车轮、车轮与地面 之间的相互影响

4 建模方法1： 要求：对轿车的上下振动进行动力学建模 缺点：模型粗糙，没有考虑人与车、车与车轮、车轮与地面 之间的相互影响 优点：模型简单 分析：人与车、车与车轮、车轮与地面之间的运动存在耦合 将车、人等全部作为一个质量考虑，并考虑弹性和阻尼

引例：轿车行驶在路面上会产生上下振动 m车 建模方法2：车、人的质量分别考虑，并考虑各自的弹性和阻尼 优点：模型较为精确，考虑了人与车之间的耦合 缺点：没有考虑车与车轮、车轮与地面之间的相互影响 5

5 建模方法2： 优点：模型较为精确，考虑了人与车之间的耦合 缺点：没有考虑车与车轮、车轮与地面之间的相互影响 车、人的质量分别考虑，并考虑各自的弹性和阻尼

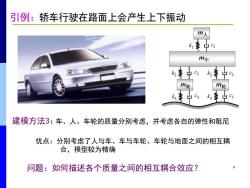
引例：轿车行驶在路面上会产生上下振动 m人 车 m轮 m轮 建模方法3：车、人、车轮的质量分别考虑，并考虑各自的弹性和阻尼 优点：分别考虑了人与车、车与车轮、车轮与地面之间的相互耦 合，模型较为精确 问题：如何描述各个质量之间的相互耦合效应？ 6

6 建模方法3： 优点：分别考虑了人与车、车与车轮、车轮与地面之间的相互耦 合，模型较为精确 问题：如何描述各个质量之间的相互耦合效应？ 车、人、车轮的质量分别考虑，并考虑各自的弹性和阻尼

主要内容 口多自由度系统的动力学方程 作用力方程（刚度矩阵质量矩阵） 位移方程（柔度矩阵） 耦合与坐标变换 口多自由度系统的自由振动 固有频率 模态（主振型） 模态正交性、主质量和主刚度 口多自由度系统的受迫振动 系统对简谐力激励的响应 动力吸振器 7 模态叠加法在受迫振动中的应用

7 主要内容

一、 多自由度系统的动力学方程 作用力方程（平动运动和转动运动） 位移方程 8

8

一、多自由度系统的动力学方程一 作用力方程 平动运动。图示双质量弹簧系统，两质量m,和m2分别受到激振 力P()和P()的作用。不计摩擦和其他形式的阻尼，试建立系 统的运动微分方程。 (t0→x K 解：建立坐标： x1,x2的原点分别取在m1,m2的静平衡位置 设某一瞬时：m和m2上分别有位移x1和x2、加速度x2

9 平动运动。图示双质量弹簧系统，两质量m1和m2分别受到激振 力P1(t)和P2(t)的作用。不计摩擦和其他形式的阻尼，试建立系 统的运动微分方程。 m1和m2上分别有位移x1和x2 1 2 设某一瞬时： 、加速度 x、x 解： , 1 x 2 x 的原点分别取在 的静平衡位置 建立坐标： 1 2 m ,m

一、多自由度系统的动力学方程一 作用力方程 P()→ P,(t) 受力分析： P(0 P(t) k2（x1-X) k2（x1-X》 m m22 建立方程： m+kx+k (x-x2)=P(t) 力量纲 m22-k2(x1-x2)+k3x2=P2(t) 10

10 建立方程： 1 1 1 1 2 1 2 1 2 2 2 1 2 3 2 2 ( ) ( ) ( ) ( ) m x k x k x x P t m x k x x k x P t              力量纲 受力分析：