西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2014)第4讲 特殊矢量场

西安电子料技等 电子工程学院DP School of Electronic Engineering,Xidian University http://see.xidian.edu.cn 场论与复变函数 主讲:徐乐 2014年9月11日星期四
场论与复变函数 主讲:徐乐 2014 年 9 月11日星期四

Review ■场论导论 ■矢量场的矢量线 单值、连续且具 ·数量场的等值面与等值线 有一阶连续偏导 ■数量场的方向导数与梯度 ■矢量场的通量与散度 ·矢量场的环量与旋度 lexu@mail.xidian.edu.cn
Review 场论导论 矢量场的矢量线 数量场的等值面与等值线 单值、连续且具 有一阶连续偏导 数量场的方向导数与梯度 矢量场的通量与散度 矢量场的环量与旋度 lexu@mail.xidian.edu.cn 2
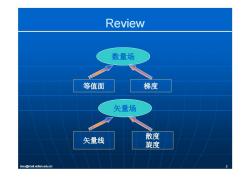
Review 数量场 等值面 梯度 矢量场 矢量线 散度 旋度 lexu@mail.xidian.edu.cn
Review 数量场 等值面 梯度 矢量场 矢量线 散度旋度 lexu@mail.xidian.edu.cn 3

Review ■通量 设AM0为一矢量场,沿其中有向曲面S正(负) 侧曲面积分称为矢量场AM)向s正(负)侧穿过 曲面S的通量。 ·如果曲面是一个开曲面,则 =小-&∫i达 ·如果曲面是一个闭曲面,则 lexu@mail.xidian.edu.cn
Review 通量 • 设A ( ) M 为 矢量场 一 ,沿其中有向曲面 沿其中有向曲面S正(负) 侧曲面积分称为矢量场A (M)向s正(负)侧穿过 曲面S的通量。 如果曲面是一个开曲面,则 A dS A dS ˆ 如果曲面是一个闭曲面,则 S S A dS A ndS 如果曲面是 个闭曲面,则 S A dS lexu@mail.xidian.edu.cn 4 S
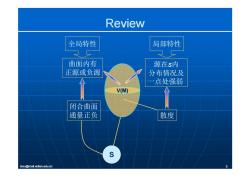
Review 全局特性 局部特性 曲面内有 源在s内 正源或负源 分布情况及 点处强弱 V(M) 闭合曲面 通量正负 散度 lexu@mail.xidian.edu.cn
Review 全局特性 局部特性 曲面内有 源在s内 V(M) 正源或负源 分布情况及 一点处强弱 闭合曲面 通量正负 散度 lexu@mail.xidian.edu.cn 5 S

Review ■散度: ● 设M是矢量场中的一点,在M的某个邻域内取 一包含M在内的任一闭合曲面,其所包含区域 的体积为△V,以△Φ表示穿出△s的通量。若 当该区域以任意方式缩向点M时, 明as 47 极限存在,则称之为矢量场在点M处的散度。 记为 H45 40 4=1 =lim AQMA △ lexu@mail.xidian.edu.cn
Review 散度: • 设M是矢量场中的 点一 ,在M的某个邻域内取 的某个邻域内取 一包含M在内的任一闭合曲面,其所包含区域 的体积为△V,以△φ表示穿出△s的通量。若 当该区域以任意方式缩向点M时, A ds 极限存在 则称之为矢量场在点M处的散度 V V s 极限存在,则称之为矢量场在点M处的散度。 记为 A ds lexu@mail.xidian.edu.cn 6 V V div A s M M lim lim
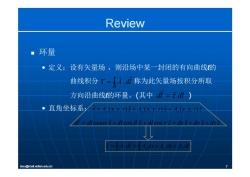
Review 。环量 。定义:设有矢量场,则沿场中某一封闭的有向曲线的 曲线积分「=4d称为此矢量场按积分所取 方向沿曲线的环量。(其中-dl-dl) 。直角坐标系4=4,+4,+4 =dl cos+dl cos B+l cosy6=d+d山)+北含 =4dl=4d本+4山+4 lexu@mail.xidian.edu.cn
Review 环量 • 定义:设有矢量场 ,则沿场中某 封闭的有向曲线 一封闭的有向曲线l的 曲线积分 称为此矢量场按积分所取 l A dl 方向沿曲线l的环量。(其中 ) • 直角坐标系: dl dl A A (x y z) xˆ A (x y z) yˆ A (x y z)zˆ • 直角坐标系:A A x y z x A x y z y A x y z z x y z ( , , ) ( , , ) ( , , ) dl dl x dl cos cos cos ˆ yˆ dl z dx x d ˆ ˆ ˆ y yˆ dz z l x y z l A dl A dx A dy A dz lexu@mail.xidian.edu.cn 7 l x y z l y
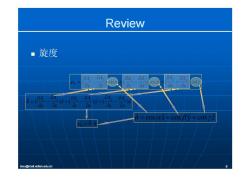
Review ■旋度 OS E n=cosax+cos By+cosy lexu@mail.xidian.edu.cn
Review 旋度 ( ) cos ( ) cos ( ) cos y A x A x A z A z A y Az y x z y x n z y A x A y x A z A x z A y A R z y x z y x ( )ˆ ( ) ˆ ( )ˆ n x yz ˆˆˆ cos cos cos ˆ ˆ n R n lexu@mail.xidian.edu.cn 8
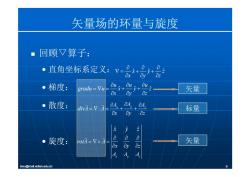
矢量场的环量与旋度 ■回顾又算子: ·直角坐标系定义: v=+0+0 。梯度: gradu Yu u+ 矢量 ·散度: dnA=又.A 6A. 标量 8x 0z 旋度: rotd Vx 4 xa pa 20论 矢量 A lexu@mail.xidian.edu.cn 9
矢量场的环量与旋度 回顾▽算子: • 直角坐标系定义: • 梯度: x y ˆ ˆ zˆ x y z ˆ ˆ ˆ uuu gradu u x y z • 梯度: 矢量 • 散度: gradu u x y z x y z x y z A A A divA A 矢量 标量 xyz ˆ ˆ ˆ 散度 divA A x y z 标量 xyz rotA A x y z • 旋度: 矢量 lexu@mail.xidian.edu.cn 9 x y z y A A A

矢量场的环量与旋度 ·旋度运算法则 1°VX(c)=cVxA(c-常数) 5°VxWw)=0 2°Vx(d±历=7x4士7x8 6°V.x方=0 3°7x(i=w7x+7wxa 7°vx7x1-W方-7a 4°V(dx)=o1.B-mti 其中V称为拉普拉斯算子,在直角坐标系中有 V2=77= a2,a2,∂2 h=0头+必品 2z2 +a V2a=2A+V249+242 lexu@mail.xidian.edu.cn 10
矢量场的环量与旋度 • 旋度运算法则 lexu@mail.xidian.edu.cn 10
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第4讲 特殊矢量场.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2016)第3讲 矢量场分析.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2014)第3讲 矢量场分析.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第3讲 矢量场分析.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2016)第2讲 数量场.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2014)第2讲 数量场.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第2讲 数量场.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2016)第1讲 矢量分析(主讲:徐乐).pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第1讲 矢量分析(主讲:徐乐).pdf
- 《MATLAB及其在理工课程中的应用指南》课程PPT教学课件(十一五规划版)第9章 在信号与系统中的应用.ppt
- 《MATLAB及其在理工课程中的应用指南》课程PPT教学课件(十一五规划版)第8章 在电工电子中的应用.ppt
- 《MATLAB及其在理工课程中的应用指南》课程PPT教学课件(十一五规划版)第7章 在力学机械中的应用.ppt
- 《MATLAB及其在理工课程中的应用指南》课程PPT教学课件(十一五规划版)第6章 在普通物理中的应用.ppt
- 《MATLAB及其在理工课程中的应用指南》课程PPT教学课件(十一五规划版)第5章 MATLAB在高等数学中的应用举例 5.6节 概率论和数理统计.ppt
- 《MATLAB及其在理工课程中的应用指南》课程PPT教学课件(十一五规划版)第5章 MATLAB在高等数学中的应用举例 5.5节 线性代数.ppt
- 《MATLAB及其在理工课程中的应用指南》课程PPT教学课件(十一五规划版)第5章 MATLAB在高等数学中的应用举例 5.4节 数字积分和微分方程数值解.ppt
- 《MATLAB及其在理工课程中的应用指南》课程PPT教学课件(十一五规划版)第5章 MATLAB在高等数学中的应用举例 5.3节 数列与级数.ppt
- 《MATLAB及其在理工课程中的应用指南》课程PPT教学课件(十一五规划版)第5章 MATLAB在高等数学中的应用举例 5.2节 解析几何与多变量分析.ppt
- 《MATLAB及其在理工课程中的应用指南》课程PPT教学课件(十一五规划版)第5章 MATLAB在高等数学中的应用举例 5.1节 函数极限和导数.ppt
- 西安电子科技大学:《线性代数实践及MATLAB入门》课程PPT教学课件(第二版)第十章 后续课矩阵建模举例.ppt
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2016)第4讲 特殊矢量场.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第5讲 哈密顿算子及正交曲线坐标系.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2014)第5讲 哈密顿算子及正交曲线坐标系.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2016)第5讲 哈密顿算子及正交曲线坐标系.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第6讲 习题课.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2014)第6讲 场论(复习课).pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第7讲 复数概论.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2014)第7讲 再看矢量运算.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第8讲 复变函数.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2014)第8讲 复数概论.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第9讲 解析函数(I).pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2014)第9讲 复数概论.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第10讲 解析函数(Ⅱ).pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2014)第10讲 解析函数(I).pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第11讲 初等函数.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2014)第11讲 解析函数(II).pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第12讲 复变函数的积分1、柯西-古萨定理1.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2014)第12讲 初等函数.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第13讲 复变函数的积分2、柯西-古萨定理2.pdf
- 西安电子科技大学:《复变函数与场论》课程教学课件(讲义,2011)第14讲 复变函数的积分3.pdf
